Exercise 4.16: Comparison between Binary PSK and Binary FSK

• Return to book

Bitfehlerwahrscheinlichkeitskurven
von binärer PSK und binärer FSK

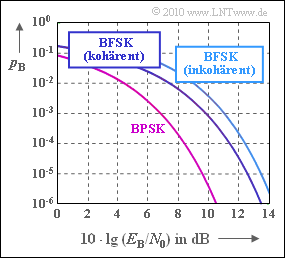
KORREKTUR: Titel "Erercise" The graph shows the bit error probability for binary  FSK modulation  $\rm (BFSK)$  in

• coherent demodulation , as well as in
• non-coherent demodulation

in comparison with  binary phase modulation  $\rm (BPSK)$.

Orthogonality is always assumed. For coherent demodulation, the modulation index can be a multiple of  $h = 0.5$ , so that the middle plot can also apply to   Minimum Shift Keying  $\rm (MSK)$ .  In contrast, for non-coherent demodulation of BFSK, the modulation index must be a multiple of  $h = 1$ .

This system comparison is once again based on the  AWGN channel , characterized by the relationship  $E_{\rm B}/N_0$. The equations for the bit error probabilities are as follows

• for Binary Phase Shift Keying  $\rm (BPSK)$:

$$p_{\rm B} = {\rm Q}\left ( \sqrt{{2 \cdot E_{\rm B}}/{N_0 }} \hspace{0.1cm}\right ) = {1}/{2}\cdot {\rm erfc}\left ( \sqrt{{E_{\rm B}}/{N_0 }} \hspace{0.1cm}\right ),$$

• for Binary Frequency Shift Keying  $\rm (BFSK)$  with coherent demodulation:

$$p_{\rm B} = {\rm Q}\left ( \sqrt{{E_{\rm B}}/{N_0 }} \hspace{0.1cm}\right ) = {1}/{2}\cdot {\rm erfc}\left ( \sqrt{{E_{\rm B}}/(2 N_0 )} \hspace{0.1cm}\right ),$$

• for Binary Frequency Shift Keying  $\rm (BFSK)$  with incoherent demodulation:

$$p_{\rm B} = {1}/{2} \cdot {\rm e}^{- E_{\rm B}/{(2N_0) }}\hspace{0.05cm}.$$

It was shown in  Exercise 4.8 , that for BPSK, the log ratio $10 · \lg \ E_{\rm B}/N_0$  must be at least  $9.6 \ \rm dB$  so that the bit error probability does not exceed  $p_{\rm B} = 10^{–5}$ .

HinTS:

• This exercise belongs to the chapter  Nonlinear_Digital_Modulation.
• However, reference is also made to the page  Linear_Digital_Modulation.

• Use the approximation  $\lg(2) ≈ 0.3$.

Questions

1

Welches  $E_{\rm B}/N_0$  (in dB) ist bei MSK und kohärenter Demodulation erforderlich, damit  $p_{\rm B} \le 10^{–5}$  zu erfüllen ist?

$10 · \lg \ E_{\rm B}/N_0 \ = \ $ $\ \rm dB$

2

Sind die folgenden Aussagen richtig:   Das gleiche Ergebnis erhält man bei

	einer FSK mit Modulationsindex  $h = 0.7$,
	einer FSK mit Modulationsindex  $h = 1$?

3

Welches  $E_{\rm B}/N_0$  (in dB) ist bei BFSK mit  $h = 1$  und inkohärenter Demodulation erforderlich, damit  $p_{\rm B} \le 10^{–5}$  zu erfüllen ist?

$10 · \lg \ E_{\rm B}/N_0 \ = \ $ $\ \rm dB$

4

Welche Bitfehlerwahrscheinlichkeit  $p_{\rm B}$  ergibt sich bei inkohärenter BFSK–Demodulation für  $10 · \lg \ E_{\rm B}/N_0 = 12.6 \ \rm dB$?

$p_{\rm B} \ = \ $ $\ \cdot 10^{-4}$

Solution

Solution

(1)  Ein Vergleich der beiden ersten Gleichungen auf der Angabenseite macht deutlich, dass bei der MSK mit kohärenter Demodulation das AWGN–Verhältnis  $E_{\rm B}/N_0$  verdoppelt werden muss, damit die gleiche Fehlerwahrscheinlichkeit wie bei BPSK erreicht wird.

• In anderen Worten:  Die kohärente BFSK–Kurve liegt um  $10 · \lg (2) ≈ 3 \ \rm dB$  rechts von der BPSK–Kurve.
• Um  $p_{\rm B} \le 10^{–5}$  zu garantieren, muss daher gelten:

$$10 \cdot {\rm lg}\hspace{0.05cm}{E_{\rm B}} /{N_{\rm 0}}= 9.6\,\,{\rm dB} + 3\,\,{\rm dB} = \underline{12.6\,\,{\rm dB}}\hspace{0.05cm}.$$

(2)  Richtig ist der Lösungsvorschlag 2:

• Die angegebene Gleichung gilt nicht nur für die MSK  $($diese ist eine FSK mit  $h = 0.5)$, sondern für jede Form von orthogonaler FSK.
• Eine solche liegt vor, wenn der Modulationsindex  $h$  ein ganzzahliges Vielfaches von  $0.5$  ist, zum Beispiel für  $h = 1$.
• Mit  $h = 0.7$  liegt keine orthogonale FSK vor. 

(3)  Aus der Umkehrfunktion der angegebenen Gleichung erhält man:

$$\frac{E_{\rm B}} {2 \cdot N_{\rm 0}}= {\rm ln}\hspace{0.05cm}\frac{1}{2 p_{\rm B}}= {\rm ln}(50000)\approx 10.82 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}{E_{\rm B}} /{N_{\rm 0}}= 21.64 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} 10 \cdot {\rm lg}\hspace{0.05cm}{E_{\rm B}}/ {N_{\rm 0}}\approx \underline{13.4\,\,{\rm dB}}\hspace{0.05cm}.$$

(4)  Aus $10 · \lg \ E_{\rm B}/N_0 = 12.6 \ \rm dB$ folgt:

$${E_{\rm B}} /{N_{\rm 0}}= 10^{1.26} \approx 16.8 \hspace{0.25cm}\Rightarrow \hspace{0.25cm} ({E_{\rm B}} /{N_{\rm 0}})/2 \approx 8.4 \hspace{0.25cm} \Rightarrow \hspace{0.25cm} p_{\rm B} = {1}/{2} \cdot {\rm e}^{- 8.4} \approx \underline{1.12 \cdot 10^{-4}}\hspace{0.05cm}.$$

Das heißt:   Bei gleichem $E_{\rm B}/N_0$ wird die Fehlerwahrscheinlichkeit bei inkohärenter Demodulation gegenüber kohärenter Demodulation (siehe Teilaufgabe 1) um etwa den Faktor 11 vergrößert.