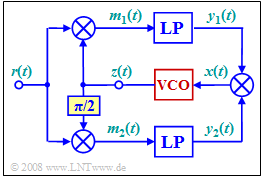
Exercise 4.9: Costas Rule Loop
An important prerequisite for coherent demodulation is in-phase carrier recovery. One possibility for this is the so-called Costas rule loop, which is shown in simplified form by the adjacent block diagram.
In binary phase modulation (BPSK), the received signal can be expressed as
- $$ r(t) = \pm s_0 \cdot \cos (2 \pi \cdot f_{\rm T} \cdot t + \phi)$$
The phase rotation $ϕ$ on the transmission channel is always assumed to be unknown. The specification "±" describes the phase jumps of the BPSK signal.
The task of the circuit indicated by the diagram is to generate a carrier signal
- $$z(t) = \cos (2 \pi \cdot f_{\rm T} \cdot t + \theta)$$
where the phase error $\phi - θ$ between the BPSK received signal $r(t)$ and the oscillation $z(t)$ generated at the receiver must be compensated.
- For this purpose, a Voltage Controlled Oscillator $($VCO$)$ is used to generate an oscillation of frequency $f_{\rm T}$, initially with arbitrary phase $θ$.
- However, the Costas rule loop iteratively achieves the desired result $θ = \phi$.
Notes:
- The exercise belongs to the chapter Linear Digital Modulation.
- In the diagram, "TP" denotes low-passes, which are assumed to be ideal.
- The square labeled $π/2$ denotes a phase rotation by $π/2 \ (90^\circ)$, so that, for example, a cosine signal becomes a minus-sine signal:
- $$\cos (\omega_{\rm 0} \cdot t)\hspace{0.3cm}\Rightarrow \hspace{0.3cm}\cos (\omega_{\rm 0} \cdot t + 90^\circ) = -\sin (\omega_{\rm 0} \cdot t)\hspace{0.05cm}.$$
- Further, the following trigonometric relations hold:
- $$\cos (\alpha) \cdot \cos (\beta) = {1} /{2} \cdot \big [ \cos (\alpha - \beta) + \cos (\alpha + \beta)\big]\hspace{0.05cm},$$
- $$\sin (\alpha) \cdot \cos (\beta) = {1} /{2} \cdot \big [ \sin (\alpha - \beta) + \sin (\alpha + \beta)\big]\hspace{0.05cm}.$$
Questions
Solution
- Using the addition theorem of trigonometry, we obtain:
- $$ m_1(t) = \pm s_0 \cdot \cos (2 \pi \cdot f_{\rm T} \cdot t + \phi) \cdot \cos (2 \pi \cdot f_{\rm T} \cdot t + \theta) = \pm \frac{s_0}{2} \cdot \left [ \cos ( \phi - \theta) + \cos (4 \pi \cdot f_{\rm T} \cdot t + \phi +\theta)\right]\hspace{0.05cm}.$$
- After the low-pass, only the DC component $y_1(t) = ± s_0/2 · \cos (\phi - θ)$ remains.
(2) Here the last solution is correct:
- Analogous to question (1), the result for the input signal of the lower low-pass filter is:
- $$ m_2(t) = \pm s_0 \cdot \cos (2 \pi \cdot f_{\rm T} \cdot t + \phi) \cdot \left [-\sin (2 \pi \cdot f_{\rm T} \cdot t + \theta) \right]= \pm \frac{s_0}{2} \cdot \left [ \sin ( \phi - \theta) + \sin (4 \pi \cdot f_{\rm T} \cdot t + \phi +\theta)\right].$$
- This leads to the following output signal:
- $$ y_2(t) = \pm {s_0}/{2} \cdot\sin ( \phi - \theta) \hspace{0.05cm}.$$
(3) Solutions 2 and 3 are correct:
- By multiplying $y_1(t)$ and $y_2(t)$ we obtain:
- $$x(t) = y_1(t) \cdot y_2(t)= \frac{s_0^2}{4} \cdot \cos ( \phi - \theta) \cdot \sin ( \phi - \theta) = \frac{s_0^2}{8} \cdot \sin ( 2\cdot\phi - 2\cdot\theta) \hspace{0.05cm}.$$
- Using the small angle approximation $\sin(α) ≈ α$ it follows:
- $$x(t) \approx \frac{s_0^2}{4} \cdot ( \phi - \theta) \hspace{0.05cm}.$$
- The rule signal $x(t)$ is thus proportional to the phase error $\phi - θ$, which is controlled to zero by the Costas rule loop.
- Thus, in the steady state, the oscillator signal $z(t)$ immediately follows the received signal $r(t)$.
- To achieve the required initial condition $θ ≈ \phi$, a training sequence is usually transmitted first and the phase is initialized accordingly.
- This is also because the phase is only controlled modulo $π$, so that, for example, $\phi - θ = π$ would incorrectly lead to the rule signal $x(t) = 0$.