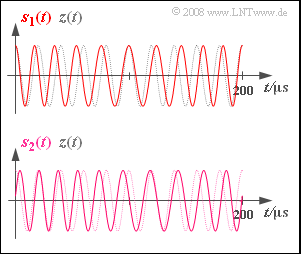
Exercise 3.1Z: Influence of the Message Phase in Phase Modulation

• Return to book

Two PM signal waveforms

We will now consider the phase modulation of diverse oscillations

$$q(t) = \cos(\omega_{\rm N} \cdot t + \phi_{\rm N})\hspace{0.05cm}.$$

The source signal is represented here in normalized form with $($amplitude  $1)$ , so that the phase-modulated signal can be characterised by the modulation index (or phase deviation)  $η$  as follows:

$$s(t) = A_{\rm T} \cdot \cos \hspace{-0.1cm}\big[\omega_{\rm T} \cdot t + \eta \cdot q(t) \big]\hspace{0.05cm}.$$

• The signal  $s_1(t)$  shown in the upper graph is characterized by the paramet values  $ϕ_{\rm N} = -90^\circ$  und  $η_1 = 2$ .
• The frequency  $f_{\rm N}$  of this sinusoidal source signal as well as the carrier frequency  $f_{\rm T}$  can be determined from the signal section of duration  $200 \ \rm µ s$  represented here.

• The signal  $s_2(t)$  possibly differs from  $s_1(t)$  due to a different message phase  $ϕ_{\rm N}$  and modulation index  $η$.  All other system parameters are unchanged from  $s_1(t)$ .

Hints:

• This exercise belongs to the chapter  Phase Modulation.
• Particular reference is made to the page Signal characteristics of phase modulation.

Questions

1

Find the frequency  $f_{\rm N}$  of the message signal.

$f_{\rm N} \ = \ $ $\ \rm kHz$

2

What is the carrier frequency $f_{\rm T}$?

$f_{\rm T} \ = \ $ $\ \rm kHz$

3

What is the maximum phase deviation  $ϕ_{\rm max}$  between  $z(t)$  and  $s(t)$?

$ϕ_{\rm max} \ = \ $ $\ \rm rad$

4

What is the maximum time shift of the zero crossings that this phase results in?

$Δt_{\rm max} \ = \ $ $\ \rm µ s$

5

Determine the modulation index  $η_2$  for the signal  $s_2(t)$.

$η_2 \ = \ $

6

What is the phase  $ϕ_{\rm N2}$  of the underlying source signal  $q(t)$ for  $s_2(t)$ ?

$ϕ_{\rm N2} \ = \ $ $\ \rm Grad$

Solution

Solution

(1)  It can be seen from the sketch that the represented section of the signal of duration  $200 \ \rm µ s$  corresponds exactly to the period duration of the sinusoidal source signal. From this follows  $f_{\rm N}\hspace{0.15cm}\underline{ = 5 \ \rm kHz}$.

• At times  $t = 0$,  $t = 100 \ \rm µ s$  and  $t = 200 \ \rm µ s$ , the signals   $z(t)$  and  $s(t)$  are synchronous in phase.
• In the first half-wave of   $q(t)$ , the zero crossings of   $s(t)$ come slightly earlier than those of the carrier signal  $z(t)$   ⇒   positive phase.
• In contrast, in the range from  $t = 100 \ \rm µ s$  to  $t = 200 \ \rm µ s$ , the phase  $ϕ(t) < 0$.

(2)  $f_{\rm T}\hspace{0.15cm}\underline{ = 50 \ \rm kHz}$, holds,

• since exactly   $10$  periods can be counted in the shown section of   $z(t)$ of duration  $200 \ \rm µ s$ .

(3)  The maximum relative phase deviation is   $ϕ_{\rm max} = η_1/(2π)\hspace{0.15cm}\underline{ ≈ 0.318}$.

(4)  Since the period of the carrier is   $T_0 = 20 \ \rm µ s$ , we obtain  $Δt_{\rm max} = ϕ_{\rm max} ·T_0\hspace{0.15cm}\underline{ ≈ 6.37 \ \rm µ s}$.

(5)  The maximum phase deviation (shift in the zero intercepts) is exactly the same for   $s_2(t)$  as for  $s_1(t)$. 

• From this, we can conclude that  $η_2 = η_1\hspace{0.15cm}\underline{ = 2}$ .

(6)  The signal  $s_2(t)$  is shifted to the right by   $25 \ \rm µ s$  compared to   $s_1(t)$ . Therefore, the same must be true for the source signals:

$$q_2(t) = q_1(t - 25\,{\rm \mu s}) = \cos \hspace{-0.1cm} \big[2 \pi f_{\rm N} (t - 25\,{\rm \mu s}) \big ] = \cos (\omega_{\rm N} \cdot t - 0.75 \cdot \pi)\hspace{0.05cm}.$$

• This corresponds to the phase position $ϕ_{\rm N2}\hspace{0.15cm}\underline{ = -135^\circ}$.