Exercise 4.11: Frequency Domain Consideration of the 4-QAM

Power-spectral densities of
BPSK and 4-QAM

Taking as our starting point $\rm BPSK$ ("binary phase modulation") with a rectangular basic pulse $g_s(t)$ of width $T_{\rm B} = 1 \ \rm µ s$ and amplitude $s_0 = 2 \ \rm V$, this exercise aims to determine the power-spectral density $\rm (PSD)$ of the 4–QAM step by step.

In Exercise 4.7, the power-spectral density ${\it Φ}_s(f)$ of the BPSK was determined for exactly these parameters. Using

$$A = s_0^2 \cdot T_{\rm B} = 4 \cdot 10^{-6}\,{\rm V^2/Hz},$$

one obtains the actual power-spectral density (in the bandpass range):

$${{\it \Phi}_s(f)} = {A}/{4} \cdot {\big [ {\rm sinc}^2( T_{\rm B}\cdot (f - f_{\rm T})) + {\rm sinc}^2( T_{\rm B}\cdot (f + f_{\rm T}))\big ]}\hspace{0.05cm}.$$

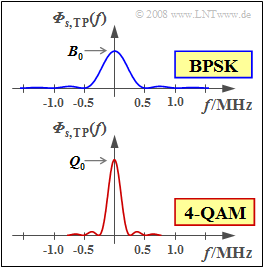
However, the top graph shows the power-spectral density ${{\it \Phi}_{s, \hspace{0.05cm}\rm TP}(f)}$ of the equivalent low-pass signal German: "äquivalentes Tiefpass–Signal" ⇒ subscript: "TP). This is obtained from ${\it Φ}_s(f)$ by

truncating all components at negative frequencies,
quadrupling the components at positive frequencies (note: a spectrum must be doubled, a PSD quadrupled),
shifting by $f_{\rm T}$ to the left:

$${{\it \Phi}_{s, \hspace{0.05cm}\rm TP}(f)} = A \cdot {\rm sinc}^2(f \cdot T_{\rm B}). \hspace{0.2cm}$$

4–QAM differs from the BPSK regarding the following details:

Splitting the binary source signal into two partial signals, each with half the bit rate, that is, with symbol duration $T = 2 · T_{\rm B}$.
Multiplication of the partial signals with cosine and minus-sine, whose amplitudes $g_0$ are each smaller than $s_0$ by a factor of $\sqrt{2}$.
Summation of the two partial signals denoted by $s_{\cos}(t)$ nd $s_{–\sin}(t)$ :

$$s(t) = s_{\rm cos}(t)+ s_{\rm -sin}(t) \hspace{0.05cm}.$$

Hints:

This exercise belongs to the chapter "Quadrature Amplitude Modulation" $\rm (QAM)$.
Reference is also made to the page "Binary Phase Shift Keying" $\rm (BPSK)$ in the previous chapter.
The power-spectral density $\rm (PSD)$ of a QAM component is identical to the comparable BPSK PSD:
Energies are to be specified in $\rm V^2s$; they thus refer to the reference resistance $R = 1 \ \rm \Omega$.

Questions

$E_{\rm B} \ = \ $

$\ \cdot 10^{-6}\ \rm V^2/Hz$

$B_0 \ = \ $

$\ \cdot 10^{-6}\ \rm V^2/Hz$

$Q_0 \ = \ $

$\ \cdot 10^{-6}\ \rm V^2/Hz$

$E_{\rm B} \ = \ $

$\ \cdot 10^{-6}\ \rm V^2/Hz$

Solution

(1) The power of the BPSK transmit signal is equal to the intergral over the power-spectral density.

If one integrates over the equivalent low-pass PSD, the factor $1/2$ must still be taken into account:

$$P_{\rm BPSK} = \int_{ - \infty }^{+\infty} {{\it \Phi}_{s}(f)}\hspace{0.1cm} {\rm d}f = \frac{1}{2} \cdot \int_{ - \infty }^{+\infty} {{\it \Phi}_{s, \hspace{0.05cm}\rm TP}(f)}\hspace{0.1cm} {\rm d}f = \frac{A}{2} \cdot \int_{ - \infty }^{+\infty} {\rm si}^2(\pi f T_{\rm B})\hspace{0.1cm} {\rm d}f = \frac{A}{2T_{\rm B}} \cdot \int_{ - \infty }^{+\infty} {\rm si}^2(\pi x)\hspace{0.1cm} {\rm d}x =\frac{A}{2T_{\rm B}}$$

$$\text{Mit} \ \ A = 4 \cdot 10^{-6}\,{\rm V^2/Hz}\hspace{0.05cm}, \hspace{0.2cm} T_{\rm B}= 10^{-6}\,{\rm s} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} P_{\rm BPSK} = 2\,{\rm V^2} ( = {s_0^2 }/{2})\hspace{0.05cm}.$$

Accordingly, the energy per bit is for BPSK:

$$E_{\rm B} = {P_{\rm BPSK} \cdot T_{\rm B}}\hspace{0.15cm}\underline {= 2 \cdot 10^{-6}\,{\rm V^2/Hz}}\hspace{0.05cm}.$$

Here again, the reference resistance is$1\ \rm Ω$.

(2) Due to the double symbol duration of 4-QAM $(T = 2 · T_{\rm B})$ , the spectral function is only half as wide as compared to BPSK, but twice as high, and instead of $s_0$ , the smaller value $g_0$ must now be considered.

The PSD value at frequency $f = 0$ is thus:

$${\it \Phi}_{s, \hspace{0.05cm}\rm cos,\hspace{0.05cm}\rm TP}(f = 0 ) = \left ({s_0}/{\sqrt{2}} \right )^2 \cdot 2 \cdot T_{\rm B} ={s_0^2 \cdot T_{\rm B}} = B_0 \hspace{0.05cm}.$$

Therefore, the result is exactly the same value as for BPSK:

$$B_0 = {\it \Phi}_{s, \hspace{0.05cm}\rm cos,\hspace{0.05cm}\rm TP}(f = 0 ) \hspace{0.15cm}\underline {= 4 \cdot 10^{-6}\,{\rm V^2/Hz}}$$

(3) The second partial signal $s_{–\sin}(t)$ yields exactly the same contribution as the signal $s_{\cos}(t)$ just considered.

Due to the orthogonality between the cosine and the minus-sine functions, the powers can be added and we get:

$$Q_0 = {\it \Phi}_{s, \hspace{0.05cm}\rm TP}(f = 0 ) = 2 \cdot B_0 \hspace{0.15cm}\underline {= 8 \cdot 10^{-6}\,{\rm V^2/Hz}}\hspace{0.05cm}.$$

(4) Analogously to in question (1) we get an energy per bit of:

$$E_{\rm B} = \frac{1}{2} \cdot T_{\rm B} \cdot \int_{ - \infty }^{+\infty} {{\it \Phi}_{s, \hspace{0.05cm}\rm TP}(f)}\hspace{0.1cm} {\rm d}f = \frac{Q_0 \cdot T_{\rm B}}{2T} \cdot \int_{ - \infty }^{+\infty} {\rm si}^2(\pi f T_{\rm B})\hspace{0.1cm} {\rm d}f = \frac{Q_0 \cdot T_{\rm B}}{2T} = \frac{8 \cdot 10^{-6}\,{\rm V^2/Hz} \cdot 1\,{\rm \mu s}}{ 2 \cdot 2\,{\rm \mu s}}\hspace{0.15cm}\underline {= 2 \cdot 10^{-6}\,{\rm V^2/Hz}}\hspace{0.05cm}.$$

It can be seen that with the assumptions made here, the "energy per bit" of BPSK and 4-QAM coincide.