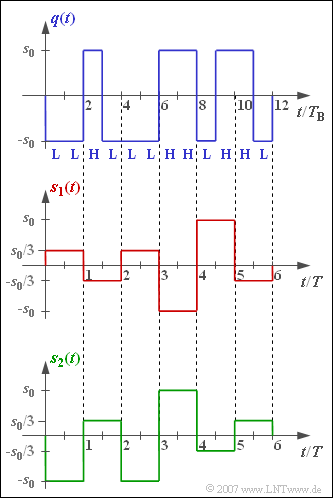
Exercise 2.4: Dual Code and Gray Code

Quaternary signals with dual and gray coding

The two shown signals $s_{1}(t)$ and $s_{2}(t)$ are two different realizations of a redundancy-free quaternary transmit signal, both derived from the blue drawn source signal $q(t)$.

For one of the transmitted signals, the so-called dual code with mapping

$$\mathbf{LL}\hspace{0.1cm}\Leftrightarrow \hspace{0.1cm} -s_0, \hspace{0.35cm} \mathbf{LH}\hspace{0.1cm}\Leftrightarrow \hspace{0.1cm} -s_0/3,\hspace{0.35cm} \mathbf{HL}\hspace{0.1cm}\Leftrightarrow \hspace{0.1cm} +s_0/3, \hspace{0.35cm} \mathbf{HH}\hspace{0.1cm}\Leftrightarrow \hspace{0.1cm} +s_0$$

was used, for the other one a certain form of a gray code. This is characterized by the fact that the binary representation of adjacent amplitude values always differ only in a single bit.

The solution of the exercise should be based on the following assumptions:

The amplitude levels are $±3\, \rm V$ and $±1 \, \rm V$.
The decision thresholds lie in the middle between two adjacent amplitude values, i.e. at $–2\, \rm V$, $0\, \rm V$ and $+2\, \rm V$.
The noise rms value $\sigma_{d}$ is to be chosen so that the distortion probability from the outer symbol $(+s_0)$ to the nearest symbol $(+s_{0}/3)$ is exactly $p = 1\%$.
Distortions to non-adjacent symbols can be excluded; in the case of Gaussian perturbations, this simplification is always allowed in practice.

One distinguishes in principle between

the symbol error probability $p_{\rm S}$ (related to the quaternary signal) and
the bit error probability $p_{B}$ (related to the binary source signal).

Notes:

The exercise is part of the chapter Basics of Coded Transmission.
Reference is also made to the chapter Redundancy-Free Coding.

For numerical evaluation of the Q–function you can use the interactive applet Complementary Gaussian Error Functions benutzen.

Questions

	$s_{1}(t)$ uses a gray coding.
	$s_{2}(t)$ uses a gray coding.

$\sigma_{d} \ = \ $

$\ \rm V$

$p_{\rm S} \ = \ $

$\ \%$

$p_{\rm B} \ = \ $

$\ \%$

$p_{\rm S} \ = \ $

$\ \%$

$p_{\rm B} \ = \ $

$\ \%$

Solution

(1) In the signal $s_{2}(t)$ one recognizes the realization of the dual code indicated at the beginning. On the other hand, in the signal $s_{2}(t)$ a gray code $\Rightarrow$ solution 1 with the following mapping was used:

$$\mathbf{HH}\hspace{0.1cm}\Leftrightarrow \hspace{0.1cm} -1, \hspace{0.35cm} \mathbf{HL}\hspace{0.1cm}\Leftrightarrow \hspace{0.1cm} -1/3, \hspace{0.35cm} \mathbf{LL}\hspace{0.1cm}\Leftrightarrow \hspace{0.1cm} +1/3, \hspace{0.35cm} \mathbf{LH}\hspace{0.1cm}\Leftrightarrow \hspace{0.1cm} +1 \hspace{0.05cm}.$$

(2) Let the probability $p$ that the amplitude value $3 \, \rm V$ falls below the adjacent decision threshold $2\, \rm V$ due to the Gaussian distributed noise with standard deviation $\sigma_{d}$ be $1\, \%$. It follows that:

$$ p = {\rm Q} \left ( \frac{3\,{\rm V} - 2\,{\rm V}} { \sigma_d}\right ) = 1 \%\hspace{0.3cm}\Rightarrow \hspace{0.3cm} {1\,{\rm V} }/ { \sigma_d} \approx 2.33 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} { \sigma_d}\hspace{0.15cm}\underline {\approx 0.43\,{\rm V}}\hspace{0.05cm}.$$

(3) The two outer symbols are each distorted with probability $p$, the two inner symbols with double probability $(2p)$. By averaging considering equal symbol occurrence probabilities, we obtain

$$p_{\rm S} = 1.5 \cdot p \hspace{0.15cm}\underline { = 1.5 \,\%} \hspace{0.05cm}.$$

(4) Each symbol error results in exactly one bit error. However, since each quaternary symbol contains exactly two binary symbols, the bit error probability is obtained:

$$p_{\rm B} = {p_{\rm S}}/ { 2}\hspace{0.15cm}\underline { = 0.75 \,\%} \hspace{0.05cm}.$$

(5) When calculating the symbol error probability $p_{\rm S}$, the mapping used is not taken into account. As in subtask (3), we obtain $p_{\rm S} \hspace{0.15cm}\underline{ = 1.5 \, \%}$.

(6) The two outer symbols are distorted with $p$ and lead to only one bit error each even with dual code.

The inner symbols are distorted with $2p$ and now lead to $1.5$ bit errors on average.
Taking into account the factor $2$ in the denominator – see subtask (2) – we thus obtain for the bit error probability of the dual code:

$$p_{\rm B} = \frac{1} { 4} \cdot \frac{p + 2p \cdot 1.5 + 2p \cdot 1.5 + p} { 2} = p \hspace{0.15cm}\underline { = 1 \,\%} \hspace{0.05cm}.$$