Exercise 3.09: Correlation Receiver for Unipolar Signaling

Example correlation values

The joint decision of $N = 3$ binary symbols (bits) by means of the correlation receiver is considered. The $M = 8$ possible source symbol sequences $Q_i$ all have the same probability and they are defined by the following unipolar amplitude coefficients:

$$Q_0 = 000, \hspace{0.15cm}Q_1 = 001,\hspace{0.15cm}Q_2 = 010,\hspace{0.15cm}Q_3 = 011 \hspace{0.05cm},\hspace{0.15cm} Q_4 = 100, \hspace{0.15cm}Q_5 = 101,\hspace{0.15cm}Q_6 = 110,\hspace{0.15cm}Q_7 = 111 \hspace{0.05cm}.$$

Further applies:

The possible transmitted signals $s_i(t)$ – each with duration $3T$ – are all rectangular with the exception of $s_0(t) \equiv 0$.
The signals $s_1(t)$, $s_2(t)$ and $s_4(t)$ with only one "$1$" each have the signal energy $E_{\rm B}$ (stands for "energy per bit"), while for example the energy of $s_7(t)$ is equal to $3E_{\rm B}$.

The correlation receiver forms from the noisy received signal $r(t) = s(t) + n(t)$ a total of $2^3 = 8$ decision variables (metrics)

$$W_i = I_i - {E_i}/{2 }\hspace{0.3cm}{\rm with}\hspace{0.3cm} I_i =\int_{0}^{3T} r(t) \cdot s_i(t) \,{\rm d} t \hspace{0.3cm}( i = 0,\text{...} , 7)$$

and sets the sinking symbol sequence $V = Q_j$, if $W_j$ is larger than all other $W_{i \ne j}$. Thus, it makes an optimal decision in the sense of maximum likelihood.

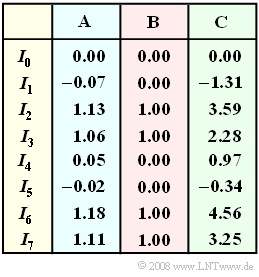
In the table, the (uncorrected) correlation values $I_0, \ \text{...} \ , I_7$ for three different systems differing in terms of noise $n(t)$ and labeled $\rm A$, $\rm B$ or $\rm C$.

One of these columns stands for "no noise",
one for "minor noise" and
another one for "strong noise".

The same source symbol sequence was always sent to determine the metrics for the three system variants.

Note:

The exercise belongs to the chapter "Optimal Receiver Strategies".

Question

	$\rm System \ A$,
	$\rm System \ B$,
	$\rm System \ C$.

$k \ = \ $

${\rm System \ A} \text{:} \hspace{0.2cm} j \ = \ $

${\rm System \ C} \text{:} \hspace{0.2cm} j \ = \ $

	$\rm System \ A$,
	$\rm System \ B$,
	$\rm System \ C$.

	The difference between $W_2$ and the next largest value $W_{i \ne 2}$ is smaller the stronger the noise is.
	When falsification occurs, the receiver is most likely to decide in favor of the symbol sequence $Q_6$.
	The probabilities for erroneous decisions in favor of $Q_0$, $Q_3$ and $Q_6$, respectively, are equal.

Solution

(1) Solution 2 is correct:

For system $\rm B$, metrics $0$ occur four times and metrics $1$ occur four times.
This points to $n(t) = 0$, otherwise – as in systems $\rm A$ and $\rm C$ – all $I_i$ would have to differ.

(2) For system $\rm B$, the decision values $W_i = I_i \ – E_i/2$, each normalized to $E_{\rm B}$, are as follows:

$$W_0 = 0 - 0 = 0, \hspace{0.2cm}W_1 = 0 - 0.5 = -0.5 \hspace{0.05cm},$$

$$W_2 = 1 - 0.5 = 0.5, \hspace{0.2cm}W_3 = 1 - 1 = 0 \hspace{0.05cm},$$

$$W_4 = 0 - 0.5 = -0.5, \hspace{0.2cm}W_5 = 0 - 1 = -1 \hspace{0.05cm}.$$

$$W_6 = 1 - 1 = 0, \hspace{0.2cm}W_7 = 1 - 1.5 = -0.5 \hspace{0.05cm}.$$

The maximum value $W_2 = 0.5$ ⇒ $i = 2$.
Thus, the correlation receiver decides to use $V = Q_2$.
Since there is no noise, $Q_2 =$ "$\rm 010$" was indeed also sent ⇒ $\underline { k= 2}$.

(3) For the decision values of system $\rm A$ holds:

$$W_0 = 0.00 - 0.00 = 0.00, \hspace{0.2cm}W_1 = -0.07 - 0.50 = -0.57, $$

$$W_2 = 1.13 - 0.50 = 0.63, \hspace{0.2cm}W_3 = 1.06 - 1.00 = 0.06 \hspace{0.05cm},$$

$$W_4 = 0.05 - 0.50 = -0.45, \hspace{0.2cm}W_5 = -0.02 - 1.00 = -1.02\hspace{0.05cm},$$

$$W_6 = 1.18 - 1.00 = 0.18, \hspace{0.2cm}W_7 = 1.11 - 1.50 = -0.39 \hspace{0.05cm}.$$

The maximum is $W_j = W_2$ ⇒ $\underline { j= 2}$.
This means that the correlation receiver also makes the correct decision $V = Q_2$ for system $\rm A$.
However, without the correction term $(– E_i/2)$, the receiver would have made the wrong decision $V = Q_6$.

(4) The correlation receiver $\rm C$ has to compare the following values:

$$W_0 = 0.00 - 0.00 = 0.00, \hspace{0.2cm}W_1 = -1.31 - 0.50 = -1.81 \hspace{0.05cm},$$

$$W_2 = 3.59 - 0.50 = 3.09, \hspace{0.2cm}W_3 = 2.28 - 1.00 = 1.28 \hspace{0.05cm},$$

$$W_4 = 0.97 - 0.50 = 0.47, \hspace{0.2cm}W_5 = -0.34 - 1.00 = -1.34 \hspace{0.05cm},$$

$$W_6 = 4.56 - 1.00 = 3.56, \hspace{0.2cm}W_7 = 3.25 - 1.50 = 1.75 \hspace{0.05cm}.$$

The maximization here gives $\underline {j = 6}$ ⇒ $V = Q_6$.

But since $Q_2$ was sent, the correlation receiver decides wrong here.
The noise is too strong.

(5) Solution 3 is correct:

The noise is greatest for system $\rm C$ and is even so great for the current received values that the correlation receiver makes an incorrect decision.

(6) Statements 1 and 3 are correct:

In the error-free case (system $\rm B$), the difference between $W_2 = 0.5$ and the next largest values $W_0 = W_3 = W_6 = 0$ is equal to $D_{\hspace{0.02cm}\rm min} =0.5$ in each case.
In system $\rm A$ (light noise), the difference between $W_2 = 0.63$ and the next largest value $W_6 = 0.18$ is still $D_{\hspace{0.02cm}\rm min} = 0.45$.
If the noise power is increased by a factor of $50$, the correlation receiver still decides correctly, but then the minimum difference $D_{\hspace{0.02cm}\rm min} = 0.16$ is significantly smaller.
For system $\rm C$, where the correlation receiver is overcharged ⇒ subtask (4), a noise power larger by a factor of 400 compared to system $\rm A$ was used as a basis.
If the correlation receiver decides the transmitted sequence $Q_2$ incorrectly, a falsification to the sequences $Q_0$, $Q_3$ and $Q_6$, respectively, is most likely, since all these three sequences differ from $Q_2$ only in one bit each.
The fact that $W_6$ is always larger than $W_0$ or $W_3$ in the described simulation is "coincidence" and should not be overinterpreted.