Bounds for Block Error Probability

Distance spectrum of a linear code

We further assume a linear and binary $(n, \hspace{0.05cm} k)$–block code $\mathcal{C}$ . A major goal of code design is to keep the "block error probability" ${\rm Pr}(\underline{u} \ne \underline{v}) = {\rm Pr}(\underline{z} \ne \underline{x})$ as low as possible. This is achieved by, among other things.

the minimum distance $d_{\rm min}$ between two codewords $\underline{x}$ and $\underline{x}\hspace{0.05cm}'$ is as large as possible, so that one can correct up to $t = ⌊(d_{\rm min}-1)/2⌋$ bit errors;

at the same time the minimum distance $d_{\rm min}$ ⇒ worst case occurs as rarely as possible, given all the allowed codewords.

$\text{Definition:}$ We denote the number of codewords $\underline{x}\hspace{0.05cm}'' \in \mathcal{C}$ with Hamming distance $i$ from the considered codeword $\underline{x}$ of the same code $\mathcal{C}$ with $W_i(\underline{x})$, where holds:

\[W_i(\underline{x}) = \big \vert \hspace{0.05cm} \left \{ \underline{x} \hspace{0.05cm}, \underline{x}{\hspace{0.05cm}' \in \hspace{0.05cm} \mathcal{C} } \hspace{0.1cm}\vert\hspace{0.1cm} d_{\rm H}(\underline{x} \hspace{0.05cm}, \hspace{0.1cm}\underline{x}\hspace{0.05cm}' ) = i \right \} \hspace{0.05cm} \big \vert\hspace{0.05cm}.\]

The straight lines of the absolute value here denote the number of codewords $\underline{x}\hspace{0.05cm}'$, that satisfy the condition $d_{\rm H}(\underline{x} \hspace{0.05cm}, \hspace{0.1cm}\underline{x}\hspace{0.05cm}' ) = i $ .

This value is also called multiplicity.

Hamming distances between all code words

$\text{Example 1:}$ We consider the $(5, \, 2)$ block code $\mathcal{C}$ with the generator matrix

\[{ \boldsymbol{\rm G} } = \begin{pmatrix} 1 &0 &1 &1 &0 \\ 0 &1 &0 &1 &1 \end{pmatrix} \hspace{0.05cm}.\]

The table shows the hamming distances

between all codewords $\underline{x}_i$.
to the reference words $\underline{x}_0$, ... , $\underline{x}_3$.

One recognizes: Independently of the reference word $\underline{x}_i$ holds:

\[W_0 = 1 \hspace{0.05cm}, \hspace{0.5cm}W_1 = W_2 = 0 \hspace{0.05cm},\hspace{0.5cm} W_3 = 2 \hspace{0.05cm},\hspace{0.5cm} W_4 = 1\]

\[ \Rightarrow\hspace{0.3cm} d_{\rm min} = 3\hspace{0.05cm}.\]

Not only in this example, but in any linear code, the same multiplicities $W_i$ result for each codeword. Furthermore, since the all-zero word $\underline{0} = (0, 0,\text{ ...} \hspace{0.05cm}, 0)$ is part of every linear binary code, the above definition can also be formulated as follows:

$\text{Definition:}$ The distance spectrum of a linear binary $(n, \hspace{0.03cm} k)$ block code is the set $\{W_i \}$ with $i = 0, 1,$ ... , $n$. Here $W_i$ gives the number of codewords $\underline{x} \in \mathcal{C}$ with Hamming weight $w_{\rm H}(\underline{x}) = i$ .

Often one describes the set $\hspace{0.05cm}\{W_i \}\hspace{0.05cm}$ also as a polynomial with a pseudovariable $X$:

\[\left \{ \hspace{0.05cm} W_i \hspace{0.05cm} \right \} \hspace{0.3cm} \Leftrightarrow \hspace{0.3cm} W(X) = \sum_{i=0 }^{n} W_i \cdot Xi^{i} = W_0 + W_1 \cdot X + W_2 \cdot X^{2} + ... \hspace{0.05cm} + W_n \cdot X^{n}\hspace{0.05cm}.\]

It is also called $W(X)$ weight enumerator function.

For example, the weight enumerator function of the $(5, \hspace{0.02cm} 2)$ code $\mathcal{C} = \left \{ \hspace{0.05cm}(0, 0, 0, 0, 0) \hspace{0.05cm},\hspace{0.15cm} (0, 1, 0, 1, 1) \hspace{0.05cm},\hspace{0.15cm}(1, 0, 1, 1, 0) \hspace{0.05cm},\hspace{0.15cm}(1, 1, 1, 0, 1) \hspace{0.05cm} \right \}$ of $\text{Example 1}$:

\[W(X) = 1 + 2 \cdot X^{3} + X^{4}\hspace{0.05cm}.\]

As can be seen from the "table of its code words" , for the $(7, \hspace{0.02cm}4, \hspace{0.02cm}3)$ Hamming code:

\[W(X) = 1 + 7 \cdot X^{3} + 7 \cdot X^{4} + X^{7}\hspace{0.05cm}.\]

The transformation of the distance spectrum $\hspace{0.01cm}\{W_i \}\hspace{0.01cm}$ into the weight enumerator function $W(X)$ also offers great numerical advantages in some exercises. For example, if the Weight Enumerator Function $W(X)$ of a $(n, \hspace{0.03cm} k)$–Block Codes $\mathcal{C}$ is known, then for the corresponding "dual" $(n, \hspace{0.03cm} n-k)$ code $\mathcal{C}_{\rm dual}$:

\[W_{\rm Dual}(X) = \frac{(1+X)^n}{2^k} \cdot W \left ( \frac{1-X}{1+X} \right )\hspace{0.05cm}.\]

$\text{Example 2:}$ The weight enumerator function $W(X)$ of "single parity–check codes" with $n = 6$, $k = 5$ ⇒ $\text{SPC (6, 5)}$.

This is obtained by comparing all $2^5 = 32$ code words with the all-zero word:

\[W_{\rm SPC\hspace{0.03cm}(6,\hspace{0.08cm}5)}(X) = 1 + 15 \cdot X^{2} + 15 \cdot X^{4} + X^{6}\hspace{0.05cm}.\]

Considering the above equation, you get the same result much faster:

The to $\text{SPC (6, 5)}$ dual code is the "repetition code" $\text{RC (6, 1)}$ with only two codewords $(0, 0, 0, 0, 0, 0)$ and $(1, 1, 1, 1, 1, 1)$:

\[W_{\rm RC\hspace{0.03cm}(6,\hspace{0.08cm}1)}(X) = 1 + X^{6}\hspace{0.05cm}.\]

From this it follows for the weight enumerator function of the $\text{SPC (6, 5)}$ according to the above equation with $k = 1$:

\[W_{\rm SPC\hspace{0.03cm}(6,\hspace{0.08cm}5)}(X) = \frac{(1+X)^6}{2^1} \cdot W \left [1 \hspace{-0.05cm}+\hspace{-0.05cm} \left ( \frac {1\hspace{-0.05cm}-\hspace{-0.05cm}X}{1\hspace{-0.05cm}+\hspace{-0.05cm}X}\right )^6 \right ] = 1/2 \cdot \big [( 1\hspace{-0.05cm}+\hspace{-0.05cm}X) ^6 \hspace{-0.05cm}+\hspace{-0.05cm} ( 1-X) ^6 \big ] = 1 \hspace{-0.05cm}+\hspace{-0.05cm} 15 \cdot X^{2} \hspace{-0.05cm}+\hspace{-0.05cm} 15 \cdot X^{4} \hspace{-0.05cm}+\hspace{-0.05cm} X^{6}\hspace{0.05cm}.\]

Union Bound of the block error probability

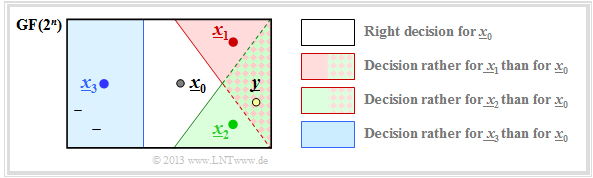
We consider as in $\text{Example 1}$ to the distance spectrum the $(5, \hspace{0.02cm} 2)$–block code $\mathcal{C} = \{\underline{x}_0, \underline{x}_1, \underline{x}_2, \underline{x}_3 \}$ and assume that the codeword $\underline{x}_0$ has been sent. The graphic illustrates the situation.

Derivation of the Union Bound

In the error-free case, the code word estimator would then return $\underline{z} = \underline{x}_0$ . Otherwise, a block error would occur (that is, $\underline{z} \ne \underline{x}_0$ and accordingly $\underline{v} \ne \underline{u}_0)$ with probability

\[{\rm Pr(block\:error)} = {\rm Pr}\left (\big [\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}1}\big ] \hspace{0.05cm}\cup\hspace{0.05cm}\big [\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}2}\big ] \hspace{0.05cm}\cup\hspace{0.05cm}\big [\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}3}\big ] \right ) \hspace{0.05cm}.\]

The event "corruption of $\underline{x}_0$ to $\underline{x}_1$" occurs for a given received word $\underline{y}$ according to the "Maximum Likelihood Decision Rule" "block-wise ML" exactly when holds for the conditional probability density function:

\[\big [\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}1}\big ] \hspace{0.3cm} \Leftrightarrow \hspace{0.3cm} f(\underline{x}_{\hspace{0.02cm}0}\hspace{0.02cm} | \hspace{0.05cm}\underline{y}) < f(\underline{x}_{\hspace{0.02cm}1}\hspace{0.02cm} | \hspace{0.05cm}\underline{y}) \hspace{0.05cm}.\]

Since $\big [\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}1}\big ] $, $\big [\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}2}\big ] $, $\big [\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}3}\big ] $are not necessarily disjoint events (which would thus be mutually exclusive), the "probability of the union set" is less than or equal to the sum of the individual probabilities:

\[{\rm Pr(block\:error)} \le {\rm Pr}\big [\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}1}\big ] \hspace{0.05cm}+\hspace{0.05cm}{\rm Pr}\big [\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}2}\big ] \hspace{0.05cm}+ \hspace{0.05cm}{\rm Pr}\big [\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}3}\big ] \hspace{0.05cm}.\]

One calls this upper bound for the (block) error probability the Union Bound. This was already used in the chapter "approximation of the error probability" of the book "Digital Signal Transmission".

We generalize and formalize these results under the assumption that both $\underline{x}$ and $\underline{x}\hspace{0.05cm}'$ belong to the code $\mathcal{C}$ .

$\text{Then the following calculation rules apply:}$

$\rm Block\:error\:probability$:

$${\rm Pr(block\:error)} = {\rm Pr} \left ( \bigcup_{\underline{x}\hspace{0.05cm}' \ne \underline{x} } \hspace{0.15cm}\big [\underline{x} \mapsto \underline{x}\hspace{0.05cm}'\big] \right )\hspace{0.05cm},$$

Upper bound after the $\text{Union Bound}$:

$${\rm Pr(Union \hspace{0.15cm}Bound)} \le \sum_{\underline{x}\hspace{0.05cm}' \ne \underline{x} } \hspace{0.15cm} {\rm Pr}\big[\underline{x} \mapsto \underline{x}\hspace{0.05cm}'\big] \hspace{0.05cm},$$

$\text{Pairwise error probability}$ (according to the MAP or ML criterion.):

$${\rm Pr}\hspace{0.02cm}\big[\underline{x} \mapsto \underline{x}\hspace{0.05cm}'\big] = {\rm Pr} \big [ f(\underline{x}\hspace{0.05cm}\vert \hspace{0.05cm}\underline{y}) \le f(\underline{x}\hspace{0.05cm}'\hspace{0.05cm} \vert \hspace{0.05cm}\underline{y}) \big ] \hspace{0.05cm}.$$

On the next pages, these results are applied to different channels.

Union Bound for the BSC model

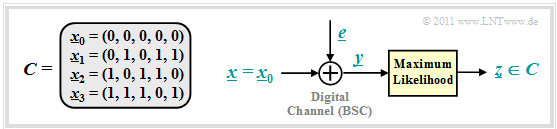
We further consider the exemplary $(5, \hspace{0.02cm} 2)$ code: $\mathcal{C} = \left \{ \hspace{0.05cm}(0, 0, 0, 0, 0) \hspace{0.05cm},\hspace{0.15cm} (0, 1, 0, 1, 1) \hspace{0.05cm},\hspace{0.15cm}(1, 0, 1, 1, 0) \hspace{0.05cm},\hspace{0.15cm}(1, 1, 1, 0, 1) \hspace{0.05cm} \right \}$ and for the digital channel we use the BSC model (Binary Symmetric Channel ):

\[{\rm Pr}(y = 1 \hspace{0.05cm} | \hspace{0.05cm}x = 0 ) = {\rm Pr}(y = 0 \hspace{0.05cm} | \hspace{0.05cm}x = 1 ) = {\rm Pr}(e = 1) = \varepsilon \hspace{0.05cm},\]

\[{\rm Pr}(y = 0 \hspace{0.05cm} | \hspace{0.05cm}x = 0 ) = {\rm Pr}(y = 1 \hspace{0.05cm} | \hspace{0.05cm}x = 1 ) = {\rm Pr}(e = 0) = 1 -\varepsilon \hspace{0.05cm}.\]

Then holds (see the following graphic):

The codewords $\underline{x}_0 = (0, 0, 0, 0, 0)$ and $\underline{x}_1 = (0, 1, 0, 1, 1)$ differ in $d = 3$ bits, where $d$ indicates the Hamming–distance between $\underline{x}_0$ and $\underline{x}_1$ .
An incorrect decoding result $\big[\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}1}\big] $ is obtained whenever at least two of the three bits at bit positions 2, 4, and 5 are corrupted.
In contrast, the bit positions 1 and 3 do not matter here, since they are the same for $\underline{x}_0$ and $\underline{x}_1$ .

BSC model and ML detection

Since the considered code $t = ⌊(d-1)/2⌋ = 1$ can correct errors, holds:

\[{\rm Pr}\big [\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}1}\big ] \hspace{-0.1cm} = \hspace{-0.1cm} \sum_{i=t+1 }^{d} {d \choose i} \cdot \varepsilon^{i} \cdot (1 - \varepsilon)^{d-i} = {3 \choose 2} \cdot \varepsilon^{2} \cdot (1 - \varepsilon) + {3 \choose 3} \cdot \varepsilon^{3} =3 \cdot \varepsilon^2 \cdot (1 - \varepsilon) + \varepsilon^3 = {\rm Pr}\big[\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}2}\big]\hspace{0.05cm}.\]

This takes into account that $\underline{x}_0 = (0, 0, 0, 0)$ and $\underline{x}_2 = (1, 0, 1, 1, 0)$ also differ in three bit positions.

The code words $\underline{x}_0 = (0, 0, 0, 0, 0)$ and $\underline{x}_3 = (1, 1, 1, 0, 1)$ on the other hand differ in four bit positions:

Wrong decoding of the block therefore certainly occurs if four or three bits are corrupted.
A corruption of two bits also results in a block error with $50$–percent probability, if one assumes a random decision for this.

\[{\rm Pr}\big[\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}3}\big] = \varepsilon^4 + 4 \cdot \varepsilon^3 \cdot (1 - \varepsilon) + {1}/{2} \cdot 6 \cdot \varepsilon^2 \cdot (1 - \varepsilon)^2 \hspace{0.05cm}.\]

This results in the "Union Bound":

\[{\rm Pr(Union \hspace{0.15cm}Bound)} = {\rm Pr}\big[\underline{x}_{\hspace{0.02cm}0} \hspace{-0.02cm}\mapsto \hspace{-0.02cm}\underline{x}_{\hspace{0.02cm}1}\big] +{\rm Pr}\big[\underline{x}_{\hspace{0.02cm}0} \hspace{-0.02cm}\mapsto \hspace{-0.02cm} \underline{x}_{\hspace{0.02cm}2}] +{\rm Pr}[\underline{x}_{\hspace{0.02cm}0} \hspace{-0.02cm}\mapsto \hspace{-0.02cm} \underline{x}_{\hspace{0.02cm}3}\big] \ge {\rm Pr(Blockfehler)} .\]

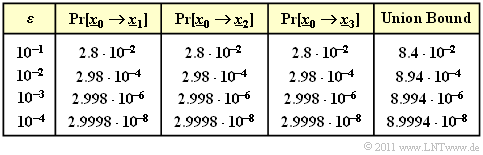
Numeric Union Bound for the $\text{(5, 2)}$ code

$\text{Beispiel 3:}$ The table summarizes the results for different values of the BSC parameter $\varepsilon$ .

It is worth mentioning that the completely different probabilities to be calculated ${\rm Pr}\big[\underline{x}_{\hspace{0.02cm}0} \hspace{-0.02cm}\mapsto \hspace{-0.02cm}\underline{x}_{\hspace{0.02cm}1}\big]$ und ${\rm Pr}\big[\underline{x}_{\hspace{0.02cm}0} \hspace{-0.02cm}\mapsto \hspace{-0.02cm}\underline{x}_{\hspace{0.02cm}3}\big]$ give exactly the same numerical result.

The upper bound according to Bhattacharyya

Another upper bound on the block error probability was given by Bhattacharyya :

\[{\rm Pr(block\:error)} \le W(X = \beta) -1 = {\rm Pr(Bhattacharyya)} \hspace{0.05cm}.\]

It should be noted that:

$W(X)$ is the above defined weight enumerator function characterizing the channel code used.

The Bhattacharyya parameter $\beta$ identifies the digital channel. For example:

\[\beta = \left\{ \begin{array}{c} \lambda \\ \sqrt{4 \cdot \varepsilon \cdot (1- \varepsilon)}\\ {\rm e}^{- R \hspace{0.05cm}\cdot \hspace{0.05cm}E_{\rm B}/N_0} \end{array} \right.\quad \begin{array}{*{1}c} {\rm for\hspace{0.15cm} das \hspace{0.15cm}BEC model},\\ {\rm for\hspace{0.15cm} das \hspace{0.15cm}BSC-Modell}, \\ {\rm for\hspace{0.15cm} das \hspace{0.15cm}AWGN model}. \end{array}\]

The Bhattacharyya bound is always (and usually significantly) above the curve for the "Union Bound". With the goal of finding a uniform bound for all channels, much coarser estimates must be made here than for the "Union Bound".

We restrict ourselves here to the Bhattacharyya bound for the BSC model. For its pairwise corruption probability was derived in front:

\[{\rm Pr}\big[\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}1}\big] = \sum_{i= \left\lfloor (d-1)/2 \right\rfloor}^{d} {d \choose i} \cdot \varepsilon^{i} \cdot (1 - \varepsilon)^{d-i} = \sum_{i= \left\lceil d/2 \right\rceil }^{d} {d \choose i} \cdot \varepsilon^{i} \cdot (1 - \varepsilon)^{d-i}\hspace{0.05cm}.\]

Here, $\varepsilon = {\rm Pr}(y = 1\hspace{0.04cm}|\hspace{0.04cm} x = 0) = {\rm Pr}(y = 0\hspace{0.04cm}|\hspace{0.04cm} x = 1)< 0.5$ denotes the channel model.
$d = d_{\rm H}(\underline{x}_0,\, \underline{x}_1)$ indicates the Hamming distance of the considered codewords.

To arrive at the Bhattacharyya bound, the following estimates must be made:

For all $i < d$ holds $\varepsilon^{i} \cdot (1 - \varepsilon)^{d-i} \le (1 - \varepsilon)^{d/2}$:

\[{\rm Pr}\big[\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}1}\big] \le \big[\varepsilon \cdot (1 - \varepsilon)\big]^{d/2} \cdot \sum_{i= \left\lceil d/2 \right\rceil }^{d} {d \choose i} \hspace{0.05cm}.\]

Change with respect to the lower limit of the run variable $i$:

\[\sum_{i= \left\lceil d/2 \right\rceil }^{d} {d \choose i} \hspace{0.15cm} < \hspace{0.15cm} \sum_{i= 0 }^{d} {d \choose i} = 2^d\hspace{0.05cm}, \hspace{0.2cm}\beta = 2 \cdot \sqrt{\varepsilon \cdot (1 - \varepsilon)} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} {\rm Pr}\big[\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}1}\big] = \beta^{d} \hspace{0.05cm}.\]

Resort according to Hamming weights $W_i$ (Hamming distance $d = i$ occurs $W_i$ times):

\[{\rm Pr(block\:error)} \hspace{0.1cm} \le \hspace{0.1cm} \sum_{i= 1 }^{n} W_i \cdot \beta^{i} = 1 + W_1 \cdot \beta + W_2 \cdot \beta^2 + \hspace{0.05cm}\text{ ...} \hspace{0.05cm}+ W_n \cdot \beta^n \hspace{0.05cm}.\]

With the weight enumerator function $W(X)= 1 + W_1 \cdot X + W_2 \cdot X^2 + \text{...} + W_n \cdot X^n$:

\[{\rm Pr(block\:error)} \le W(X = \beta) -1= {\rm Pr(Bhattacharyya)} \hspace{0.05cm}.\]

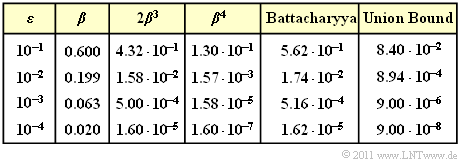
Comparison between "Union Bound" and "Bhattacharyya Barrier" valid for the BSC model

$\text{Example 4:}$ The table summarizes the Bhattacharyya results for different values of the BSC parameter $\varepsilon$ valid for the example $\text{(5, 2)}$ code.

For this one applies:

$$W_0 = 1, \ \ W_1 = W_2 = 0, \ \ W_3 = 2, \ \ W_4 = 1$$

$$\Rightarrow\hspace{0.3cm} W(X) = 1 + 2 \cdot X^3 + X^4.$$

Thus, the Bhattacharyya bound can be calculated:

\[ {\rm Pr(Bhattacharyya)} = W(\beta) -1 = 2 \cdot \beta^3 + \beta^4\hspace{0.05cm}.\]

This provides a (often rough) bound on the block error probability:

\[ {\rm Pr(block\:error)} \le {\rm Pr(Bhattacharyya)} \hspace{0.05cm}.\]

$\text{Conclusion:}$ Based on the $\text{Example 3}$ and the $\text{Example 4}$ (on this page) for the simple $\text{(5, 2)}$ block code, though of little practical relevance, and in anticipation of the $\text{example 5}$ (on the next page) for the $\text{(7, 4, 3)}$ Hamming code, we summarize:

The block error probability of a coding system is often not analytically specifiable and must be determined by simulation. The same applies to the bit error probability.

The Union Bound provides an upper bound for the block error probability. For many applications (especially short codes) the Union Bound is only slightly above the actual error probability.

The Bhattacharyya bound for the BEC channel is about a factor $2$ above the Union Bound – see Exercise 1.14. For the BSC– and the AWGN channel, the gap is much larger. The factor $10$ (and more) is not uncommon.

The Bhattacharyya bound $W(\beta) - 1$ looks very simple at first sight. Nevertheless, one needs also here knowledge about the exact weight function $W(\xi)$ of the code.

If the transmission channel (BEC, BSC, AWGN or variations thereof) and its parameters are known, there is nothing to be said against using the (more accurate) "Union Bound" as an upper bound for the block error probability.

Bounds for the (7, 4, 3) Hamming code at the AWGN channel

Finally, we consider the block error probability and its bounds ("Union Bound" and "Bhattacharyya bound" ) for the following configuration:

AWGN channel, characterized by the quotient $E_{\rm B}/N_0$,
Hamming code $\text{HC(7, 4, 3)}$ ⇒ $R = 4/7$, $W(X)-1 = 7 \cdot X^3 + 7 \cdot X^4 + X^7$,
"Soft Decision" according to the maximum likelihood criterion.

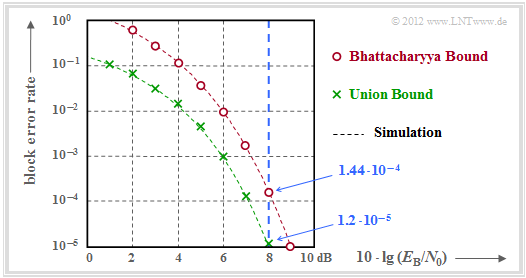
Block error probability and bounds of $\text{HC (7, 4, 3)}$

$\text{Example 5:}$ The results are summarized in the graph.

In contrast to the graph in the section Coding gain – bit error rate with AWGN, the block error rate is given here and not the bit error rate.
Approximately, the latter is smaller by the factor $d_{\rm min}/k$ if, as here $d_{\rm min}< k$ . In the present example $d_{\rm min}/k = 0.75$.
Only the points for integer $\rm dB$ values were calculated. The dashed lines were interpolated.
The (blue) numerical values given on the right are for $10 \cdot \lg \, E_{\rm B}/N_0 = 8 \, \rm dB$ ⇒ $E_{\rm B}/N_0 \approx 6.31$ (blue vertical).

The green crosses mark the "Union Bound". After this applies:

\[{\rm Pr(block\:error)} \le \sum_{i= d_{\rm min} }^{n} W_i \cdot {\rm Q} \left ( \sqrt{i \cdot {2R \cdot E_{\rm B} }/{N_0} } \right ) \]

\[\Rightarrow \hspace{0.3cm}{\rm Pr(block\:error)} \approx 7 \cdot {\rm Q} (4.65) + 7 \cdot {\rm Q} (5.37) + {\rm Q} (7.10) = \]

\[\hspace{4.0cm} \approx 7 \cdot 1.66 \cdot 10^{-6} + 7 \cdot 3.93 \cdot 10^{-8}+ 10^{-9} = 1.2 \cdot 10^{-5} \hspace{0.05cm}.\]

The numerical values make it clear that the Union Bound is essentially determined by the first term:

\[{\rm Pr(Union\hspace{0.15cm} Bound)} \approx W_{d_{\rm min} } \cdot {\rm Q} \left ( \sqrt{d_{\rm min} \cdot {2R \cdot E_{\rm B} }/{N_0} } \right ) = 1.16 \cdot 10^{-5} \hspace{0.05cm}.\]

However, this so-called "Truncated Union Bound" is no longer a true bound for the block error probability in all applications, but is to be understood as an approximation.
The Bhattacharyya bound is marked by red dots in the graph. This is well above the Union Bound due to the highly simplified Chernoff–Rubin Bound ${\rm Q}(x) \le {\rm e}^{-x^2/2}$ .
For example, for $10 \cdot \lg \, E_{\rm B}/N_0 = 8 \, \rm dB$ with $\beta = {\rm e}^{-R \hspace{0.05cm}\cdot \hspace{0.05cm}E_{\rm B}/N_0} \approx 0.027$ compared to the Union Bound a more than tenfold value:

\[{\rm Pr(Bhattacharyya)} = W(\beta) -1 = 7 \cdot \beta^3 + 7 \cdot \beta^4 + \beta^7 \approx 1.44 \cdot 10^{-4} \hspace{0.05cm}.\]

Exercises for the chapter

Exercise 1.14: Bhattacharyya Bound for BEC

Exercise 1.15: Distance Spectra of HC (7, 4, 3) and HC (8, 4, 4)

Exercise 1.16: Block Error Probability Bounds for AWGN

Exercise 1.16Z: Bounds for the Gaussian Error Function