Exercise 1.1: ISDN Supply Lines

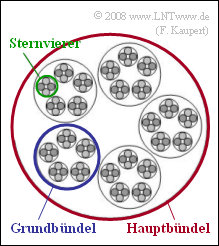
Main bundle, basic bundle, and star quad

In ISDN (Integrated Services Digital Network) the final branch (near the subscriber) is connected to a local exchange (OVSt) by a copper twisted pair, whereby two twisted pairs are twisted into a so-called star quad. Several such star quads are then combined to form a basic bundle, and several basic bundles are combined to form a main bundle (see graphic).

In the network of Deutsche Telekom (formerly: Deutsche Bundespost), mostly copper lines with 0.4 mm core diameter are found, for whose attenuation and phase function the following equations are given in [PW95]:

$$\frac{a_{\rm K}(f)}{\rm dB} = \left [ 5.1 + 14.3 \cdot \left (\frac{f}{\rm MHz}\right )^{0.59}\right ]\cdot\frac{l}{\rm km} \hspace{0.05cm},$$

$$\frac{b_{\rm K}(f)}{\rm rad} = \left [ 32.9 \cdot \frac{f}{\rm MHz} + 2.26 \cdot \left (\frac{f}{\rm MHz}\right )^{0.5}\right ]\cdot\frac{l}{\rm km} \hspace{0.05cm}.$$

Hierbei bezeichnet $l$ die Leitungslänge.

Hinweise:

Die Aufgabe gehört zum Kapitel "General Description of ISDN".
Insbesondere wird Bezug genommen auf die Seite Netzinfrastruktur für das ISDN.
Weitere Informationen zur Dämpfung von Kupferleitungen finden Sie im Kapitel "Eigenschaften elektrischer Leitungen" des Buches Lineare zeitinvariante Systeme.
[PW95] bezieht sich auf die folgende Veröffentlichung: Pollakowski, P.; Wellhausen, H.-W.: Eigenschaften symmetrischer Ortsanschlusskabel im Frequenzbereich bis 30 MHz. Deutsche Telekom AG, Forschungs- und Technologiezentrum Darmstadt, 1995.

Fragebogen

$N \ = \ $

	Die beiden Übertragungsrichtungen stören sich gegenseitig.
	Es kann zu Nebensprechstörungen kommen.
	Es treten Impulsinterferenzen auf.

$l \ = \ $

$\ \rm km$

$a_{\rm K}(f = 120 \ \rm kHz) \ = \ $

$\ \rm dB$

$b_{\rm K}(f = 120 \ \rm kHz) \ = \ $

$\ \rm rad$

Musterlösung

Solution

(1) Im Anschlussbereich wird eine Zweidrahtübertragung verwendet. Die möglichen Anschlüsse sind gleich der Anzahl der Doppeladern im Hauptkabel: $\underline{N = 50}$.

(2) Richtig sind die Lösungsvorschläge 1 und 2:

Bei Zweidrahtübertragung ist ein Richtungstrennungsverfahren erforderlich, nämlich die so genannte Gabelschaltung. Diese hat die Aufgabe, dass beim Empfänger $\rm A$ nur das Sendesignal von Teilnehmer $\rm B$ ankommt, nicht jedoch das eigene Sendesignal. Dies gelingt bei schmalbandigen Signalen – zum Beispiel Sprache – im allgemeinen recht gut, jedoch nicht vollständig.
Aufgrund von induktiven und kapazitiven Kopplungen kann es zu Übersprechen von der im gleichen Sternvierer befindlichen Doppelader kommen, wobei Nahnebensprechen (das heißt: der störende Sender und der gestörte Empfänger liegen örtlich zusammen) zu größeren Beeinträchtigungen führt als Fernnebensprechen.
Nicht zutreffend ist dagegen der letzte Lösungsvorschlag. Impulsinterferenzen – also die gegenseitige störende Beeinflussung benachbarter Symbole – können zwar durchaus auftreten, hängen aber nicht mit der Zweidrahtübertragung zusammen. Der Grund hierfür sind vielmehr (lineare) Verzerrungen aufgrund des spezifischen Dämpfungs– und Phasenverlaufs.

(3) Die Gleichsignal–Dämpfung um den Faktor $4$ kann wie folgt ausgedrückt werden:

$$a_{\rm K}(f = 0) = 20 \cdot {\rm lg}\,\,(4) = 12.04\,{\rm dB}\hspace{0.05cm}.$$

Mit dem angegebenen Koeffizienten $\text{5.1 dB/km}$ ergibt sich somit die Leitungslänge $l = 12.04/5.1\hspace{0.15cm}\underline{ = 2.36 \ \rm km}$.

(4) Mit den angegebenen Gleichungen und $ l = 2.36 \ \rm km$ erhält man:

$$a_{\rm K}(f = 120\,{\rm kHz})= (5.1 + 14.3 \cdot 0.12^{\hspace{0.05cm}0.59}) \cdot 2.36\,{\rm dB} \hspace{0.15cm}\underline{\approx 21.7\,{\rm dB}}\hspace{0.05cm},$$

$$b_{\rm K}(f = 120\,{\rm kHz}) = (32.9 \cdot 0.12 + 2.26 \cdot 0.12^{\hspace{0.05cm}0.5}) \cdot 2.36\,{\rm rad}\hspace{0.15cm}\underline{ \approx 11.2\,{\rm rad}}\hspace{0.05cm}.$$