Discrete Fouriertransform and Inverse

Open Applet in new Tab Deutsche Version Öffnen

Applet Description

The conventional Fourier Transform $\rm (FT)$ allows the calculation of the spectral function $X(f)$ of a time continuous signal $x(t)$.

In contrast, the Discrete Fourier Transform $\rm (DFT)$ is limited to a time discrete signal, represented by $N$ time domain coefficients $d(\nu)$ with indices $\nu = 0, \text{...} , N\hspace{-0.1cm}-\hspace{-0.1cm}1$, which can be interpreted as equidistant samples of the time continuous signal $x(t)$.

If the "sampling theorem" is fulfilled, the DFT algorithm likewise allows the calculation of $N$ frequency domain coefficients $D(\mu)$ with indices $\mu = 0, \text{...} , N\hspace{-0.1cm}-\hspace{-0.1cm}1$. These are equidistant samples of the frequency continuous spectrum $X(f)$.

The applet illustrates the properties of the $\text{DFT:}\hspace{0.3cm}d(\nu)\hspace{0.1cm} \Rightarrow \hspace{0.1cm} D(\mu)$ by using the example $N=16$. The default $d(\nu)$–assignments KORREKTUR: $d(\nu)$ assignments for the DFT are:

(a) According to the input field, (b) Constant signal, (c) Complex exponential function (of time), (d) Harmonic oscillation (with $($Phase $\varphi = 45^\circ)$,

(e) Cosine signal (one period), (f) Sinusoidal signal (one period), (g) Cosine signal (two periods), (h) Alternating time coefficients, (i) Dirac impulse,

(j) Rectangular impulse, (k) Triangular impulse, (l) Gaussian impulse.

Possible $D(\mu)$–assignments KORREKTUR: $D(\mu)$ assignments for the Inverse Discrete Fourier Transform ⇒ $\text{IDFT:}\hspace{0.3cm}D(\mu)\hspace{0.1cm} \Rightarrow \hspace{0.1cm} d(\nu)$ are:

(A) According to the input field, (B) Constant spectrum, (C) Complex exponential function (of frequency), (D) Equivalent to setting (d) in the time domain,

(E) Cosine spectrum (one frequency period), (F) Sinusoidal spectrum (one frequency period), (G) Cosine spectrum (two frequency periods),

(H) Alternating spectral coefficients, (I) Dirac spectrum, (J) Rectangular spectrum, (K) Triangular spectrum, (L) Gaussian spectrum.

The applet uses the framework Plot.ly.

Theoretical Background

Arguments for the discrete realization of the Fourier transform

The Fourier transform according to the conventional description for continuous-time signals has an infinitely high selectivity due to the unlimited extension of the integration interval and is therefore an ideal theoretical tool for spectral analysis.

If the spectral components $X(f)$ of a time function $x(t)$ are to be determined numerically, the general transformation equations

$$\begin{align*}X(f) & = \int_{-\infty }^{+\infty}x(t) \cdot {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi f t}\hspace{0.1cm} {\rm d}t\hspace{0.5cm} \Rightarrow\hspace{0.5cm} \text{Inward transformation}\hspace{0.7cm} \Rightarrow\hspace{0.5cm} \text{First Fourier integral} \hspace{0.05cm},\\ x(t) & = \int_{-\infty }^{+\infty}\hspace{-0.15cm}X(f) \cdot {\rm e}^{\hspace{0.05cm}+{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi f t}\hspace{0.1cm} {\rm d}f\hspace{0.35cm} \Rightarrow\hspace{0.5cm} \text{Backward transformation}\hspace{0.4cm} \Rightarrow\hspace{0.5cm} \text{Second Fourier integral} \hspace{0.05cm}\end{align*}$$

are unsuitable for two reasons:

The equations apply exclusively to continuous-time signals. With digital computers or signal processors, however, only discrete-time signals can be processed.
For a numerical evaluation of the two Fourier integrals it is necessary to limit the respective integration interval to a finite value.

$\text{This results in the following consequence:}$

A continuous signal must undergo two processes before the numerical determination of its spectral properties, viz.

sampling for discretization, and
windowing to limit the integration interval.

In the following, starting from an aperiodic time function $x(t)$ and the corresponding Fourier spectrum $X(f)$, a discrete-time and discrete-frequency description suitable for computer processing is presented.

Time discretization – periodization in the frequency domain

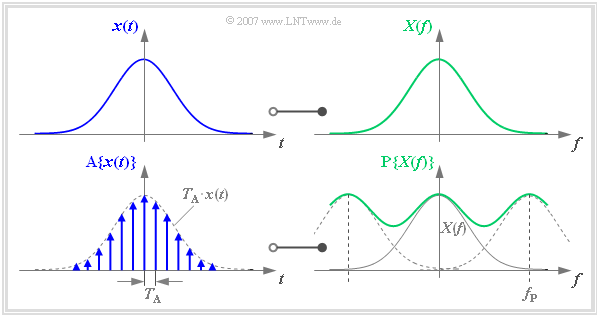
The following graphs uniformly show the time domain on the left and the frequency domain on the right. Without restriction of generality, $x(t)$ and $X(f)$ are real and Gaussian, respectively.

Discretization in the time domain – periodization in the frequency domain

One can describe the sampling of the time signal $x(t)$ by multiplication with a Dirac pulse $p_{\delta}(t)$. This results in the time signal sampled at distance $T_{\rm A}$

$${\rm A}\{x(t)\} = \sum_{\nu = - \infty }^{+\infty} T_{\rm A} \cdot x(\nu \cdot T_{\rm A})\cdot \delta (t- \nu \cdot T_{\rm A} )\hspace{0.05cm}.$$

We now transform this sampled signal $\text{A}\{ x(t)\}$ into the frequency domain. The multiplication of the Dirac pulse $p_{\delta}(t)$ with $x(t)$ corresponds in the frequency domain to the convolution of $P_{\delta}(f)$ with $X(f)$. The periodized spectrum $\text{P}\{ X(f)\}$ is obtained, where $f_{\rm P}$ is the frequency period of the function $\text{P}\{ X(f)\}$:

$${\rm A}\{x(t)\} \hspace{0.2cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \hspace{0.2cm} {\rm P}\{X(f)\} = \sum_{\mu = - \infty }^{+\infty} X (f- \mu \cdot f_{\rm P} )\hspace{0.5cm} {\rm with }\hspace{0.5cm}f_{\rm P}= {1}/{T_{\rm A}}\hspace{0.05cm}.$$

We call the sampled signal $\text{A}\{ x(t)\}$.
The frequency period is denoted by $f_{\rm P}$ = $1/T_{\rm A}$.

The graph above shows the functional relationship described here. It should be noted:

The frequency period $f_{\rm P}$ was deliberately chosen small here so that the overlap of the spectra to be summed can be clearly seen.
In practice, due to the sampling theorem, $f_{\rm P}$ should be at least twice as large as the largest frequency contained in the signal $x(t)$.
If this is not fulfilled, aliasing must be expected.

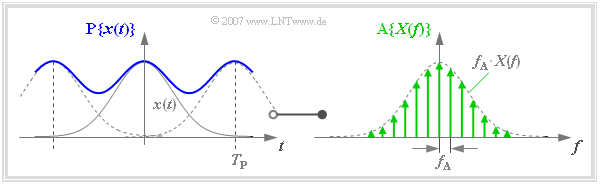
Frequency discretization – periodization in the time domain

The discretization of $X(f)$ can also be described by a multiplication with a Dirac pulse. The result is the spectrum sampled at distance $f_{\rm A}$:

$${\rm A}\{X(f)\} = X(f) \cdot \sum_{\mu = - \infty }^{+\infty} f_{\rm A} \cdot \delta (f- \mu \cdot f_{\rm A } ) = \sum_{\mu = - \infty }^{+\infty} f_{\rm A} \cdot X(\mu \cdot f_{\rm A } ) \cdot\delta (f- \mu \cdot f_{\rm A } )\hspace{0.05cm}.$$

Transforming the frequency Dirac pulse used here $($with pulse weights $f_{\rm A})$ into the time domain, we obtain with $T_{\rm P} = 1/f_{\rm A}$:

$$\sum_{\mu = - \infty }^{+\infty} f_{\rm A} \cdot \delta (f- \mu \cdot f_{\rm A } ) \hspace{0.2cm}\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\, \hspace{0.2cm} \sum_{\nu = - \infty }^{+\infty} \delta (t- \nu \cdot T_{\rm P } ) \hspace{0.05cm}.$$

The multiplication with $X(f)$ corresponds in the time domain to the convolution with $x(t)$. The signal $\text{P}\{ x(t)\}$ periodized at distance $T_{\rm P}$ is obtained:

$${\rm A}\{X(f)\} \hspace{0.2cm}\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\, \hspace{0.2cm} {\rm P}\{x(t)\} = x(t) \star \sum_{\nu = - \infty }^{+\infty} \delta (t- \nu \cdot T_{\rm P } )= \sum_{\nu = - \infty }^{+\infty} x (t- \nu \cdot T_{\rm P } ) \hspace{0.05cm}.$$

Discretization in the frequency domain – periodization in the time domain

$\text{Example 1:}$ This relationship is illustrated in the graphic:

Due to the coarse frequency rastering, this example results in a relatively small value for the time period $T_{\rm P}$.

Therefore, the (blue) periodized time signal $\text{P}\{ x(t)\}$ differs significantly from $x(t)$ due to overlaps.

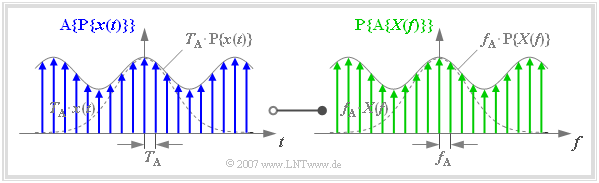
Finite signal representation

Finite signals of the Discrete Fourier Transform

One arrives at the so-called finite signal representation

when both the time function $x(t)$ and
the spectral function $X(f)$

are specified exclusively by their sample values.
The graph is to be interpreted as follows:

In the left picture the function $\text{A}\{ \text{P}\{ x(t)\}\}$ is drawn in blue. It is obtained by sampling the periodized time function $\text{P}\{ x(t)\}$ with equidistant Dirac pulses in the distance $T_{\rm A} = 1/f_{\rm P}$.
In the right picture the function $\text{P}\{ \text{A}\{ X(f)\}\}$ is drawn in green. This results from periodization $($with $f_{\rm P})$ of the sampled spectral function $\{ \text{A}\{ X(f)\}\}$.
There is also a Fourier correspondence between the blue finite signal and the green finite signal, as follows:

$${\rm A}\{{\rm P}\{x(t)\}\} \hspace{0.2cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \hspace{0.2cm} {\rm P}\{{\rm A}\{X(f)\}\} \hspace{0.05cm}.$$

However, the Diraclines of the periodic continuation $\text{P}\{ \text{A}\{ X(f)\}\}$ of the sampled spectral function fall into the same frequency grid as those of $\text{A}\{ X(f)\}$ only if the frequency period $f_{\rm P}$ is an integer multiple $(N)$ of the frequency sampling interval $f_{\rm A}$.

When using the finite signal representation, the following condition must always be fulfilled, where in practice a power of two is usually used for the natural number $N$ (the graph above is based on the value $N = 8$ ):

$$f_{\rm P} = N \cdot f_{\rm A} \hspace{0.5cm} \Rightarrow\hspace{0.5cm} {1}/{T_{\rm A} }= N \cdot f_{\rm A} \hspace{0.5cm} \Rightarrow\hspace{0.5cm} N \cdot f_{\rm A}\cdot T_{\rm A} = 1\hspace{0.05cm}.$$

Bei Einhaltung der Bedingung $N \cdot f_{\rm A} \cdot T_{\rm A} = 1$ ist die Reihenfolge von Periodifizierung und Abtastung vertauschbar. Somit gilt:

$${\rm A}\{{\rm P}\{x(t)\}\} = {\rm P}\{{\rm A}\{x(t)\}\}\hspace{0.2cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \hspace{0.2cm} {\rm P}\{{\rm A}\{X(f)\}\} = {\rm A}\{{\rm P}\{X(f)\}\}\hspace{0.05cm}.$$

$\text{Fazit:}$

Die Zeitfunktion $\text{P}\{ \text{A}\{ x(t)\}\}$ besitzt die Periode $T_{\rm P} = N \cdot T_{\rm A}$.
Die Periode im Frequenzbereich ist $f_{\rm P} = N \cdot f_{\rm A}$.
Zur Beschreibung des diskretisierten Zeit– und Frequenzverlaufs reichen somit jeweils $N$ komplexe Zahlenwerte in Form von Impulsgewichten aus.

$\text{Beispiel 2:}$ Es liegt ein zeitbegrenztes (impulsartiges) Signal $x(t)$ in abgetasteter Form vor, wobei der Abstand zweier Abtastwerte $T_{\rm A} = 1\, {\rm µ s}$ beträgt:

Nach einer diskreten Fouriertransformation mit $N = 512$ liegt das Spektrum $X(f)$ in Form von Abtastwerten im Abstand $f_{\rm A} = (N \cdot T_{\rm A})^{–1} \approx 1.953\,\text{kHz} $ vor.
Vergrößert man den DFT–Parameter auf $N= 2048$, so ergibt sich ein feineres Frequenzraster mit $f_{\rm A} \approx 488\,\text{Hz}$.

Diskrete Fouriertransformation

Aus dem herkömmlichen "ersten Fourierintegral"

$$X(f) =\int_{-\infty }^{+\infty}x(t) \cdot {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi \hspace{0.05cm}\cdot \hspace{0.05cm} f \hspace{0.05cm}\cdot \hspace{0.05cm}t}\hspace{0.1cm} {\rm d}t$$

entsteht durch Diskretisierung $(\text{d}t \to T_{\rm A}$, $t \to \nu \cdot T_{\rm A}$, $f \to \mu \cdot f_{\rm A}$, $T_{\rm A} \cdot f_{\rm A} = 1/N)$ die abgetastete und periodifizierte Spektralfunktion

$${\rm P}\{X(\mu \cdot f_{\rm A})\} = T_{\rm A} \cdot \sum_{\nu = 0 }^{N-1} {\rm P}\{x(\nu \cdot T_{\rm A})\}\cdot {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi \hspace{0.05cm} \cdot \hspace{0.05cm}\nu \hspace{0.05cm} \cdot \hspace{0.05cm}\mu /N} \hspace{0.05cm}.$$

Es ist berücksichtigt, dass aufgrund der Diskretisierung jeweils die periodifizierten Funktionen einzusetzen sind.

Aus Gründen einer vereinfachten Schreibweise nehmen wir nun die folgenden Substitutionen vor:

Die $N$ Zeitbereichskoeffizienten seien mit der Laufvariablen $\nu = 0$, ... , $N - 1$:

$$d(\nu) = {\rm P}\left\{x(t)\right\}{\big|}_{t \hspace{0.05cm}= \hspace{0.05cm}\nu \hspace{0.05cm}\cdot \hspace{0.05cm}T_{\rm A}}\hspace{0.05cm}.$$

Die $N$ Frequenzbereichskoeffizienten seien mit der Laufvariablen $\mu = 0,$ ... , $N$ – 1:

$$D(\mu) = f_{\rm A} \cdot {\rm P}\left\{X(f)\right\}{\big|}_{f \hspace{0.05cm}= \hspace{0.05cm}\mu \hspace{0.05cm}\cdot \hspace{0.05cm}f_{\rm A}}\hspace{0.05cm}.$$

Abkürzend wird für den von $N$ abhängigen komplexen Drehfaktor geschrieben:

$$w = {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi /N} = \cos \left( {2 \pi}/{N}\right)-{\rm j} \cdot \sin \left( {2 \pi}/{N}\right) \hspace{0.05cm}.$$

Zur Definition der Diskreten Fouriertransformation (DFT) mit $N=8$

$\text{Definition:}$

Unter dem Begriff Diskrete Fouriertransformation (kurz DFT) versteht man die Berechnung der $N$ Spektralkoeffizienten $D(\mu)$ aus den $N$ Signalkoeffizienten $d(\nu)$:

$$D(\mu) = \frac{1}{N} \cdot \sum_{\nu = 0 }^{N-1} d(\nu)\cdot {w}^{\hspace{0.05cm}\nu \hspace{0.03cm} \cdot \hspace{0.05cm}\mu} \hspace{0.05cm}. $$

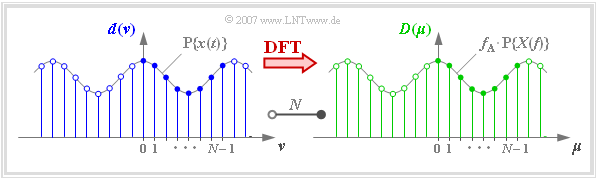
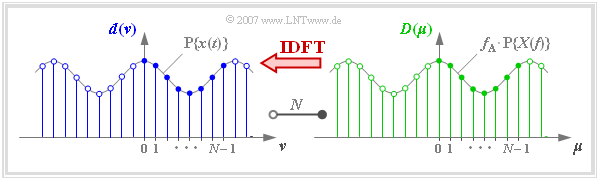
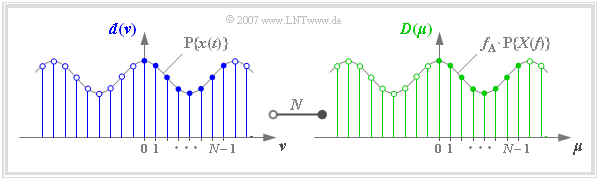
In der Grafik erkennt man an einem Beispiel

die $N = 8$ Signalkoeffizienten $d(\nu)$ an der blauen Füllung,
die $N = 8$ Spektralkoeffizienten $D(\mu)$ an der grünen Füllung.

Inverse Diskrete Fouriertransformation

Die Inverse Diskrete Fouriertransformation (IDFT) beschreibt das "zweite Fourierintegral"

$$\begin{align*}x(t) & = \int_{-\infty }^{+\infty}X(f) \cdot {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi \hspace{0.05cm}\cdot \hspace{0.05cm} f \hspace{0.05cm}\cdot \hspace{0.05cm} t}\hspace{0.1cm} {\rm d}f\end{align*}$$

in diskretisierter Form: $d(\nu) = {\rm P}\left\{x(t)\right\}{\big|}_{t \hspace{0.05cm}= \hspace{0.05cm}\nu \hspace{0.05cm}\cdot \hspace{0.05cm}T_{\rm A}}\hspace{0.01cm}.$

Zur Definition der IDFT mit $N=8$

$\text{Definition:}$

Unter dem Begriff Inverse Diskrete Fouriertransformation (kurz IDFT) versteht man die Berechnung der Signalkoeffizienten $d(\nu)$ aus den Spektralkoeffizienten $D(\mu)$:

$$d(\nu) = \sum_{\mu = 0 }^{N-1} D(\mu) \cdot {w}^{-\nu \hspace{0.03cm} \cdot \hspace{0.05cm}\mu} \hspace{0.05cm}.$$

Mit den Laufvariablen $\nu = 0, \hspace{0.05cm}\text{...} \hspace{0.05cm}, N-1$ und $\mu = 0, \hspace{0.05cm}\text{...} \hspace{0.05cm}, N-1$ gilt auch hier:

$$d(\nu) = {\rm P}\left\{x(t)\right\}{\big \vert}_{t \hspace{0.05cm}= \hspace{0.05cm}\nu \hspace{0.05cm}\cdot \hspace{0.05cm}T_{\rm A} }\hspace{0.01cm},$$

$$D(\mu) = f_{\rm A} \cdot {\rm P}\left\{X(f)\right\}{\big \vert}_{f \hspace{0.05cm}= \hspace{0.05cm}\mu \hspace{0.05cm}\cdot \hspace{0.05cm}f_{\rm A} } \hspace{0.01cm},$$

$$w = {\rm e}^{- {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi /N} \hspace{0.01cm}.$$

Ein Vergleich zwischen DFT und IDFT zeigt, dass genau der gleiche Algorithmus verwendet werden kann. Die einzigen Unterschiede der IDFT gegenüber der DFT sind:

Der Exponent des Drehfaktors ist mit unterschiedlichem Vorzeichen anzusetzen.
Bei der IDFT entfällt die Division durch $N$.

Interpretation von DFT und IDFT

Die Grafik zeigt die diskreten Koeffizienten im Zeit– und Frequenzbereich zusammen mit den periodifizierten zeitkontinuierlichen Funktionen.

Zeit– und Frequenzbereichskoeffizienten der DFT

Bei Anwendung von DFT bzw. IDFT ist zu beachten:

Nach obigen Definitionen besitzen die DFT–Koeffizienten $d(ν)$ und $D(\mu)$ stets die Einheit der Zeitfunktion.
Dividiert man $D(\mu)$ durch $f_{\rm A}$, so erhält man den Spektralwert $X(\mu \cdot f_{\rm A})$.
Die Spektralkoeffizienten $D(\mu)$ müssen stets komplex angesetzt werden, um auch ungerade Zeitfunktionen berücksichtigen zu können.
Um auch Bandpass–Signale im äquivalenten Tiefpass–Bereich transformieren zu können, verwendet man meist auch komplexe Zeitkoeffizienten $d(\nu)$.
Als Grundintervall für $\nu$ und $\mu$ definiert man meist – wie in obiger Grafik – den Bereich von $0$ bis $N - 1$.
Mit den komplexwertigen Zahlenfolgen $\langle \hspace{0.1cm}d(\nu)\hspace{0.1cm}\rangle = \langle \hspace{0.1cm}d(0), \hspace{0.05cm}\text{...} \hspace{0.05cm} , d(N-1) \hspace{0.1cm}\rangle$ sowie $\langle \hspace{0.1cm}D(\mu)\hspace{0.1cm}\rangle = \langle \hspace{0.1cm}D(0), \hspace{0.05cm}\text{...} \hspace{0.05cm} , D(N-1) \hspace{0.1cm}\rangle$ werden DFT und IDFT ähnlich wie die herkömmliche Fouriertransformation symbolisiert:

$$\langle \hspace{0.1cm} D(\mu)\hspace{0.1cm}\rangle \hspace{0.2cm}\bullet\!\!-\!\!\!-(N)\!-\!\!\!-\!\!\hspace{0.05cm}\circ\, \hspace{0.2cm} \langle \hspace{0.1cm} d(\nu) \hspace{0.1cm}\rangle \hspace{0.05cm}.$$

Ist die Zeitfunktion $x(t)$ bereits auf den Bereich $0 \le t \lt N \cdot T_{\rm A}$ begrenzt, dann geben die von der IDFT ausgegebenen Zeitkoeffizienten direkt die Abtastwerte der Zeitfunktion an: $d(\nu) = x(\nu \cdot T_{\rm A}).$
Ist $x(t)$ gegenüber dem Grundintervall verschoben, so muss man die im $\text{Beispiel 3}$ gezeigte Zuordnung zwischen $x(t)$ und den Koeffizienten $d(\nu)$ wählen.

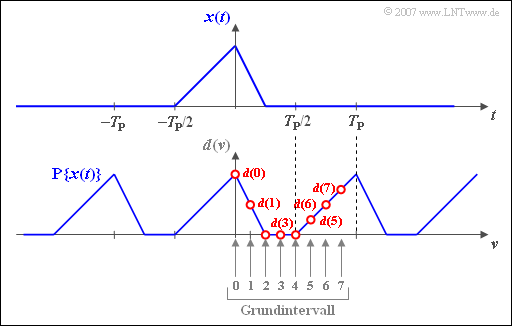
$\text{Beispiel 3:}$ Die obere Grafik zeigt den unsymmetrischen Dreieckimpuls $x(t)$, dessen absolute Breite kleiner ist als $T_{\rm P} = N \cdot T_{\rm A}$.

Zur Belegung der DFT-Koeffizienten mit $N=8$

Die untere Skizze zeigt die zugeordneten DFT–Koeffizienten gültig für $N = 8$

Für $\nu = 0,\hspace{0.05cm}\text{...} \hspace{0.05cm} , N/2 = 4$ gilt $d(\nu) = x(\nu \cdot T_{\rm A})$:

$$d(0) = x (0)\hspace{0.05cm}, \hspace{0.15cm} d(1) = x (T_{\rm A})\hspace{0.05cm}, \hspace{0.15cm} d(2) = x (2T_{\rm A})\hspace{0.05cm}, $$

$$d(3) = x (3T_{\rm A})\hspace{0.05cm}, \hspace{0.15cm} d(4) = x (4T_{\rm A})\hspace{0.05cm}.$$

Dagegen sind die Koeffizienten $d(5)$, $d(6)$ und d$(7)$ wie folgt zu setzen:

$$d(\nu) = x \big ((\nu\hspace{-0.05cm} - \hspace{-0.05cm} N ) \cdot T_{\rm A}\big ) $$

$$ \Rightarrow \hspace{0.2cm}d(5) = x (-3T_{\rm A})\hspace{0.05cm}, \hspace{0.35cm} d(6) = x (-2T_{\rm A})\hspace{0.05cm}, \hspace{0.35cm} d(7) = x (-T_{\rm A})\hspace{0.05cm}.$$

Exercises

First select the number (1,...) of the exercise.
A description of the exercise will be displayed.
The parameter values are adjusted.
Solution after pressing "Show solution".
The number 0 corresponds to a "Reset":

Same setting as at program start.

Output of a "reset text" with further explanations about the applet.

(1) New setting: DFT of signal $\rm (b)$: Constant signal. Interpret the result in the frequency domain. What is the analogon of the conventional Fourier transform?

All coefficients in the time domain are $d(\nu)=1$. Thus all $D(\mu)=0$ with the exception of $\textrm{Re}[D(0)]=1$.
This corresponds to the conventional (time-continuous) Fourier Transform: $x(t)=A\hspace{0.15cm} \circ\!\!\!-\!\!\!-\!\!\!-\!\!\bullet\hspace{0.15cm} X(f)=A\cdot \delta (f=0)$ with $A=1$.

(2) Assume the obtained $D(\mu)$ field and shift all coefficients one entry down. Which time function does the IDFT provide?

Now all $D(\mu)=0$, except for $\textrm{Re}[D(1)]=1$. The result in the time domain is a complex exponential function.
The real part of the $d(\nu)$-field KORREKTUR: $d(\nu)$ field shows a cosine and the imaginary part a sine function. For each function one can see one period respectively.

(3) Add the following coefficient to the current $D(\mu)$ field: $\textrm{Im}[D(1)]=1$. What are the differences compared to (2) in the time domain?

On the one hand, a phase shift of two support values can now be detected for the real and the imaginary parts. This corresponds to the phase $\varphi = 45^\circ$.
On the other hand, the amplitudes of the real and the imaginary part were each increased by the factor $\sqrt{2}$.

(4) Set the $D(\mu)$ field to zero except for $\textrm{Re}[D(1)]=1$. Which additional $D(\mu)$ coefficient yields a real $d(\nu)$ field?

By trial and error, one can see that $\textrm{Re}[D(15)]=1$ must apply additionally. Then the $d(\nu)$ field describes a cosine.
The following applies to the conventional (time continuous) Fourier Transform: $x(t)=2\cdot \cos(2\pi \cdot f_0 \cdot t)\hspace{0.15cm}\circ\!\!\!-\!\!\!-\!\!\!-\!\!\bullet\hspace{0.15cm} X(f)=\delta (f-f_0)+\delta (f+f_0)$.
The entry $D(1)$ is representative of the frequency $f_0$ and due to the periodicity with $N=16$ the frequency $-f_0$ is expressed by $D(15)=D(-1)$.

(5) According to the IDFT in the $d(\nu)$ field, by which $D(\mu)$ field does one obtain a real cosine function with the amplitude $A=1$?

Like the conventional Fourier transform the discrete Fourier Transform is linear ⇒ $D(1)=D(15)=0.5$.

(6) New setting: DFT of signal $\rm (e)$: Cosine signal and subsequent signal shifts. What are the effects of these shifts in the frequency domain?

A shift in the time domain changes the cosine signal to a "harmonic oscillation" with arbitrary phase.
The $D(\mu)$ field is still zero except for $D(1)$ and $D(15)$. The absolute values $|D(1)|$ and $|D(15)|$ also remain the same.
The only change concerns the phase, i.e. the different distribution of the absolute values between the real and imaginary part.

(7) New setting: DFT of signal $\rm (f)$: Sinusoidal signal. Interpret the result in the frequency domain. What is the analogon of the conventional Fourier Transform?

The sine signal results from the cosine signal by applying four time shifts. Therefore all statements of (6) are still valid.
For the conventional (time continuous) Fourier transform it holds that $x(t)= \sin(2\pi \cdot f_0 \cdot t)\hspace{0.15cm}\circ\!\!\!-\!\!\!-\!\!\!-\!\!\bullet\hspace{0.15cm} X(f)=j/2 \cdot [\delta (f+f_0)-\delta (f-f_0)]$.
The coefficient $D(1)$ $\Rightarrow$ $($frequency: $+f_0)$ is imaginary and has the imaginary part $-0.5$. Accordingly, $\textrm{Im}[D(15)]=+0.5$ ⇒ $($frequency: $-f_0)$ applies.

(8) New setting: DFT of signal $\rm (g)$: Cosine signal (two periods). Interpret the result in comparison to task KORREKTUR: exercise (5).

Here the time continuous Fourier transform reads $x(t)=\cos(2\pi \cdot (2 f_0) \cdot t)\hspace{0.15cm}\circ\!\!\!-\!\!\!-\!\!\!-\!\!\bullet\hspace{0.15cm}X(f)=0.5 \cdot \delta (f- 2 f_0)+0.5 \cdot \delta (f+ 2 f_0)$.
$D(2)$ is representative of the frequency $2 f_0$. Due to the periodicity, $D(14)=D(-2)$: $D(2)=D(14)=0.5$ is representative of the frequency $-2 f_0$.

(9) Now examine the case DFT of a sinodial signal (two periods). Which modifications do you need to make in the time domain? Interpret the result.

The desired signal can be obtained from the DFT of signal $\rm (g)$: Cosine signal (two periods) with two shifts. With the result of (7): Four shifts.
The DFT result is accordingly $\textrm{Im}[D(2)]=-0.5$ and $\textrm{Im}[D(14)]=+0.5$.

(10) New setting: DFT of signal $\rm (h)$: Alternating time coefficients. Interpret the DFT result.

Here, the time continuous Fourier transform is given by: $x(t)=\cos(2\pi \cdot (8 f_0) \cdot t)\hspace{0.15cm}\circ\!\!\!-\!\!\!-\!\!\!-\!\!\bullet\hspace{0.15cm} X(f)=0.5 \cdot \delta (f- 8 f_0)+0.5 \cdot \delta (f+ 8 f_0)$.
$8 f_0$ is the highest frequency that can be displayed with $N=16$ in the DFT. There are only two sampled values per period, namely $+1$ and $-1$.
Difference to exercise (5): $D(1)=0.5$ now becomes $D(8)=0.5$. Likewise, $D(15)=0.5$ is shifted to $D(8)=0.5$. Final result: $D(8)=1$.

(11) What are the differences between the two settings DFT from signal $\rm (i)$: Dirac impulse and IDFT from spectrum $\rm (I)$: Dirac spectrum?

None! In the first case, all coefficients are $D(\mu)=1$ (real); in the second case, however, equivalently $d(\nu)=1$ (real).

(12) Are there differences in shifting the real "$1$" in the according input fields by one place at a time, that is for $d(\nu = 1)=1$ and $D(\mu = 1)=1$?

The first case $\Rightarrow$ $\textrm{Re}[d(\nu = 1)]=1$ results in the complex exponential function in the frequency domain given by $X(f)= \textrm{e}^{-{\rm j}\hspace{0.05cm}\cdot\hspace{0.05cm} 2 \pi\hspace{0.05cm}\cdot\hspace{0.05cm} f/f_0}$ with negative sign.
The second case $\Rightarrow$ $\textrm{Re}[D(\mu = 1)]=1$ results in the complex exponential function in the time domain given by $x(t)= \textrm{e}^{+{\rm j}\hspace{0.05cm}\cdot\hspace{0.05cm} 2 \pi\hspace{0.05cm}\cdot\hspace{0.05cm} f_0\cdot t}$ with positive sign.
Note: With $\textrm{Re}[D(\mu=15)]=1$ the result in the time domain would also be a complex exponential function $x(t)= \textrm{e}^{-{\rm j}\hspace{0.05cm}\cdot\hspace{0.05cm} 2 \pi\hspace{0.05cm}\cdot\hspace{0.05cm} f_0\hspace{0.05cm}\cdot\hspace{0.05cm} t}$ with negative sign.

(13) New setting: DFT of signal $\rm (k)$: Triangle impulse. Interpret the $d(\nu)$ assignment under the assumption $T_\textrm{A} = 1$ ms.

Change the display to "absolute value". $x(t)$ is symmetrical around $t=0$ and extends from $-8 \cdot T_\textrm{A} = -8$ ms to $+8 \cdot T_\textrm{A}= +8$ ms.
$d(\nu)$ assignment: $d(0)=x(0)=1$, $d(1)=x(T_\textrm{A})=0.875$, ... , $d(8)=x(8 T_\textrm{A})=0$, $d(9)=x(-7 T_\textrm{A})=0.125$, ... , $d(15)=x(-T_\textrm{A})=0.875$.

(14) Same setting as (13). Interpret the DFT result, especially the coefficients $D(0)$, $D(1)$, $D(2)$ and $D(15)$.

In the frequency range $D(0)$ stands for the frequency $f=0$ and $D(1)$ and $D(15)$ for the frequencies $\pm f_\textrm{A}$. It holds that $f_\textrm{A}= 1/ (N\cdot T_\textrm{A})=62.5$ Hz.
For the value of the continuous spectrum at $f=0$ the following applies: $X(f=0)=D(0)/f_\textrm{A} = 0.5/ (0.0625$ kHz$)=8\cdot \textrm{kHz}^{-1}$.
The first zero of the $\textrm{si}^2$–shaped spectrum $X(f)$ occurs at $2\cdot f_\textrm{A} = 125$ Hz. The other zeros are equidistant.

(15) New setting: DFT of signal $\rm (i)$: Rectangular impulse. Interpret the displayed results.

The set (symmetrical) rectangle extends over $\pm 4 \cdot T_\textrm{A}$. At the edges, the time coefficients are only half as large: $d(4)=d(12)=0.5$.
The further statements of (14) also apply to this $\textrm{si}$–shaped spectrum $X(f)$.

(16) Same setting as for (15). Which modifications need to be made in the $d(\nu)$ field, to have the duration of the rectangle $\Rightarrow$ $\pm 2 \cdot T_\textrm{A}$.

$d(0) = d(1) = d(15) =1, \ d(2) = d(14) = 0.5$. All other time coefficients zero ⇒ first zero of the ${\rm si}$ spectrum at $4 \cdot f_{\rm A}= 250\text{ Hz}$.

(17) New setting: IDFT of spectrum $\rm (L)$: Gaussian spectrum. Interpret the result in the time domain.

Here, the time function $x(t)$ is Gaussian with the maximum $x(t=0)=4$. For the spectrum the following applies: $X(f=0)=D(0)/f_\textrm{A} = 16 \cdot \textrm{kHz}^{-1}$.
The equivalent duration of the impulse is $\Delta t = X(f=0)/x(t=0)=4\text{ ms}$. The inverse value gives the equivalent bandwidth $\Delta f = 1/\Delta t = 250\text{ Hz}$.

Applet Manual

(A) Zeitbereich (Eingabe- und Ergebnisfeld)

(B) (A)–Darstellung numerisch, grafisch, Betrag

(C) Frequenzbereich (Eingabe- und Ergebnisfeld)

(D) (C)–Darstellung numerisch, grafisch, Betrag

(E) Auswahl: DFT $(t \to f)$ oder IDFT $(f \to t)$

(F) Vorgegebene $d(\nu)$–Belegungen (falls DFT), oder

Vorgegebene $D(\mu)$–Belegungen (falls IDFT)

(G) Eingabefeld auf Null setzen

(H) Eingabefeld zyklisch nach unten (bzw. oben) verschieben

( I ) Bereich für die Versuchsdurchführung: Aufgabenauwahl

(J) Bereich für die Versuchsdurchführung: Aufgabenstellung

(K) Bereich für die Versuchsdurchführung: Musterlösung einblenden

Vorgegebene $d(\nu)$–Belegungen (für DFT):

(a) entsprechend Zahlenfeld, (b) Gleichsignal, (c) Komplexe Exponentialfunktion der Zeit, (d) Harmonische Schwingung $($Phase $\varphi = 45^\circ)$,

(e) Cosinussignal (eine Periode), (f) Sinussignal (eine Periode), (g) Cosinussignal (zwei Perioden), (h) Alternierende Zeitkoeffizienten,

(i) Diracimpuls, (j) Rechteckimpuls, (k) Dreieckimpuls, (l) Gaußimpuls.

Vorgegebene $D(\mu)$–Belegungen (für IDFT):

(A) entsprechend Zahlenfeld, (B) Konstantes Spektrum, (C) Komplexe Exponentialfunktion der Frequenz, (D) äquivalent zur Einstellung (d) im Zeitbereich ,

(E) Cosinussignal (eine Frequenzperiode), (F) Sinussignal (eine Frequenzperiode), (G) Cosinussignal (zwei Frequenzperioden), (H) Alternierende Spektralkoeffizienten,

(I) Diracspektrum, (J) Rechteckspektrum, (K) Dreieckspektrum, (L) Gaußspektrum.

About the Authors

This interactive calculation tool was designed and implemented at the Institute for Communications Engineering at the Technical University of Munich.

The first version was created in 2008 by Thomas Großer as part of his diploma thesis with “FlashMX – Actionscript” (Supervisor: Günter Söder).

Last revision and English version 2020/2021 by Carolin Mirschina in the context of a working student activity. Translation using DEEPL.com.

Die Umsetzung dieses Applets auf HTML 5 wurde durch Studienzuschüsse der Fakultät EI der TU München finanziell unterstützt. Wir bedanken uns.

Once again: Open Applet in new Tab