Exercise 3.6: State Transition Diagram

Simple realization of a rate $1/2$ convolutional encoder

A description possibility for convolutional encoders is provided by the so-called "state transition diagram".

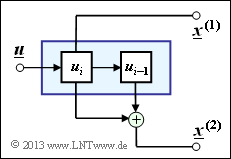
If the encoder contains $m$ memory registers ⇒ influence length $\nu = m + 1$, then there are different states $S_{\mu}$ with $0 ≤ \mu ≤ 2^m -1$, where holds for the index:

$$\mu = \sum_{l = 1}^{m} \hspace{0.1cm}2^{l-1} \cdot u_{i-l} \hspace{0.05cm}.$$

This type of code description is to be applied to the convolutional coder of rate $R = 1/2$ outlined above.

Hints:

This exercise belongs to the chapter "Code Description with State and Trellis Diagram".

Reference is made in particular to the section "State definition for a memory register".

Questions

Solution

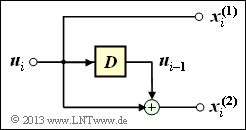
Equivalent circuit diagram of the encoder under consideration

(1) As can be seen from the accompanying equivalent circuit diagram, the encoder contains only one memory element
⇒ Memory $m = 1$. Thus there are $2^m \ \underline{= 2}$ states, viz.

the state $S_0 \ \Rightarrow \ u_{i–1} = 0$,
the state $S_1 \ \Rightarrow \ u_{i–1} = 1$.

(2) From each state $2^k = 2$ arrows go to different states.

Since there are only two states, the answer YES is correct.

(3) Correct are the solutions 1 and 3:

The information bit $u_i$ present at time $i$ is, with respect to the following time $(j = i + 1)$, the previous bit $(u_{j–1})$.
Thus $s_{i+1} = u_i$ holds. Only with $u_i = 0$ does one get from $s_i = S_1$ to $s_{i+1} = S_0$ ⇒ Proposed solution 1.
From $s_i = S_1$ ⇒ $u_{i–1} = 1$ follows further ⇒ Proposed solution 3:

$${x}_i^{(1)} = u_i = 0\hspace{0.05cm},\hspace{0.2cm}{x}_i^{(2)} = u_i + u_{i-1}= 0+1 = 1 \hspace{0.3cm}\Rightarrow \hspace{0.3cm}\underline{x}_i = (0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm}) \hspace{0.05cm}. $$

The proposed solution 4 could have been ruled out from the beginning. The graph on the specification sheet clearly shows that the coder is systematic: $x_i^{(1)} = u_i$. The combination $u_i = 0$ and $\underline{x}_i = (1, 0)$ would contradict this.

State and trellis diagram for the encoder under consideration.

(4) Correct are the solutions 2 and 4:

Using a similar solution path as in subtask (3), one arrives at the result that here the current information bit must be $u_i = 1$.
The corresponding code sequence is $\underline{x}_i = (10)$.
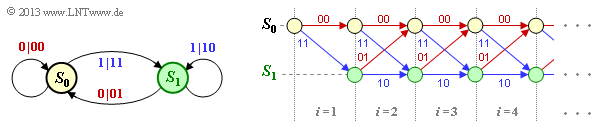
This results in the following state transition diagram (left) and the trellis diagram that can be derived from it:
Red arrows indicate the information bit $u_i = 0$, while blue arrows indicate $u_i = 1$.

(5) Both proposed solutions are correct. There are no other constraints (except binary) for the information sequences.

(6) Correct is the proposed solution 1. Starting from the state $S_0$ one arrives at.

with $u_1 = 1$ to the state $S_1$, output "$11$",
with $u_2 = 1$ to the state $S_1$, output "$10$",
with $u_3 = 0$ to state $S_0$, output "$01$",
with $u_4 = 0$ to state $S_0$, output "$00$",
with $u_5 = 1$ to state $S_1$, output "$11$",
with $u_6 = 1$ to the state $S_1$, output "$10$".

In contrast, the second code sequence is not possible:

The output "$11$" means that one started at $S_0$ and comes with $u_1 = 1$ to the state $S_1$.
But in the state $S_1$ then only the outputs "$01$" and "$10$" are possible, but not "$00$".

	The current information bit must be $u_i = 0$ .
	The current information bit must be $u_i = 1$ .
	The associated code sequence is $\underline{x}_i = (01)$.
	The associated code sequence is $\underline{x}_i = (10)$.

	The current information bit must be $u_i = 0$ .
	The current information bit must be $u_i = 1$ .
	The associated code sequence is $\underline{x}_i = (01)$.
	The associated code sequence is $\underline{x}_i = (10)$.

	$\underline{u} = (1, \, 1, \, 0, \, 0, \, 1 \, 1, \, \text{...}\hspace{0.05cm})$,
	$\underline{u} = (1, \, 0, \, 1, \, 0, \, 1, \, 0, \, \text{...}\hspace{0.05cm})$.

	$\underline{x} = (11, \, 10, \, 01, \, 00, \, 11, \, 10, \, \text{...}\hspace{0.05cm})$,
	$\underline{x} = (11, \, 00, \, 10, \, 01, \, 11, \, 00, \, \text{...}\hspace{0.05cm})$.

	Yes.
	No.