Exercise 3.3Z: GSM 900 and GSM 1800

• Return to book

$\rm GSM \ 900$  and  $\rm GSM \ 1800$

The mobile communications standard established in Europe since $1992$  $\rm GSM$  (Global System for Mobile Communications)  uses frequency and time division multiplexing to enable multiple users to communicate in one cell.

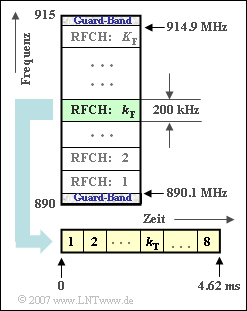
The following are important characteristics of the system shown in the diagram  $\rm GSM \ 900$  in somewhat simplified form.

• The frequency band of the uplink (the connection from the mobile to the base station) is between  $890\ \rm MHz$  and  $915 \ \rm MHz$.
• Taking into account the guard bands at both ends, a total bandwidth of  $24.8 \ \rm MHz$ is thus available for the uplink.
• This band is used by a total of  $K_{\rm F}$  subchannels (Radio Frequency Channels), which are adjacent to each other with respective frequency spacing  $200 \ \rm kHz$ . The numbering is done with the run variable  $k_{\rm F}$.
• The frequency range for the downlink (the connection from the base station to the mobile station) is located around the duplex spacing  $45 \ \rm MHz$  above the uplink and is otherwise structured in the same way as the latter.
• Each of these FDMA subchannels is used simultaneously by  $K_{\rm T} = 8$  subscribers in time division multiple access  (TDMA).

The GSM $1800$ system is structured in a similar way, but with the following differences:

• The frequency range of the uplink is between  $1710 \ \rm MHz$  and  $1785 \ \rm MHz$.
• The duplex spacing is  $95 \ \rm MHz$.

Hints:

• This exercise belongs to the chapter  "Radio Interface".
• Reference is made in particular to the page  "Realization of FDMA and TDMA".

Questions

1

How many subchannels are created in the $\rm GSM \ 900$  by frequency division multiplexing?

$K_{\rm F} \ = \ $

2

How many frequency channels are there in the  $\rm GSM \ 1800$?

$K_{\rm F} \ = \ $

3

What center frequency is used by the frequency channel numbered  $k_{\rm F} = 200$  in the downlink of  $\rm GSM \ 1800$?

$f_{\rm M} \ = \ $ $ \ \rm MHz$

4

How many subscribers  $K$  can be active at the  $\rm GSM \ 1800$  same time?

$K \ = \ $

Solution

Solution

(1)  From the total bandwidth of $25 \ {\rm MHz}\ (800 \text{...} 915 \ \rm MHz)$, the two guard bands of $100 \ \rm kHz$ each at the edges, and the channel spacing $200 \ \rm kHz$, we get for the $\rm GSM \ 900$:

$$K_{\rm F} = \frac{ 914.9 \,{\rm MHz}- 890.1 \,{\rm MHz}}{0.2 \,{\rm MHz}} \hspace{0.15cm} \underline {= 124}\hspace{0.05cm}.$$

(2)  At $\rm GSM \ 1800$, a bandwidth of $75 \ \rm MHz$ is now available in each direction.

• Taking into account the two guard bands and the same channel spacing $200 \ \rm kHz$, we obtain here:

$$K_{\rm F} = \frac{ 75 \,{\rm MHz}- 0.2 \,{\rm MHz}} \hspace{0.15cm} \underline {= 374}\hspace{0.05cm}.$$

(3)  For $\rm GSM \ 1800$, the uplink starts at $1710 \ \rm MHz$ and the downlink starts at.

$$1710 \,{\rm MHz}\,\,({\rm uplink})+ 95 \,{\rm MHz}\,\,({\rm duplex spacing}) ={1805 \,{\rm MHz}} \hspace{0.05cm}.$$

• The first downlink channel $(k_{\rm F} = 1)$ is higher by the center frequency $f_{\rm M} = 1805.2 \ \rm MHz$,
• the channel numbered $k_{\rm F} = 200$ is higher by the frequency spacing $199 \cdot 0.2 \rm MHz$:

$$f_{\rm M} (k_{\rm F} = 200) \hspace{0.15cm} \underline { = {1845 \,{\rm MHz}} \hspace{0.05cm}.$$

(4)  Using the result of subtask (2) and $K_{\rm T} = 8$, we obtain:

$$K ({\rm GSM \hspace{0.15cm}1800}) = 374 \cdot 8 \hspace{0.15cm} \underline { = 2992}\hspace{0.05cm}.$$