Speech Coding

1. Examples of Communication Systems
2. GSM – Global System for Mobile Communications
3. Speech Coding

• Previous page
• Next page

• Previous page
• Next page

Various voice coding methods

Each GSM subscriber has a maximum net data rate of  $\text{22.8 kbit/s}$  available,  while the ISDN fixed network operates with a data rate of  $\text{64 kbit/s}$  $($with  $8$  bit quantization$)$  or  $\text{104 kbit/s}$  $($with $13$ bit quantization$)$  respectively. 

• The task of  "voice coding"  $($"speech coding"$)$  in GSM is to limit the amount of data for speech signal transmission to  $\text{22.8 kbit/s}$  and to reproduce the speech signal at the receiver side in the best possible way.

• The functions of the GSM encoder and the GSM decoder are usually combined in a single functional unit called  "codec".

Different signal processing methods are used for voice coding and decoding:

• The  GSM Fullrate Vocoder  was standardized in 1991 from a combination of three compression methods for the GSM radio channel.  It is based on  "Linear Predictive Coding"  $\rm (LPC)$  in conjunction with  "Long Term Prediction"  $\rm (LTP)$  and  "Regular Pulse Excitation"  $\rm (RPE)$.

• The  GSM Halfrate Vocoder  was introduced in 1994 and provides the ability to transmit speech at nearly the same quality in half a traffic channel  $($data rate  $\text{11.4 kbit/s})$.

• The  Enhanced Full Rate Vocoder  $\rm (EFR\ codec)$  was standardized and implemented in 1995,  originally for the North American DCS1900 network.  The EFR codec provides better voice quality compared to the conventional full rate codec.

• The  Adaptive Multi-Rate Codec  $\rm (AMR\ codec)$  is the latest voice codec for GSM.  It was standardized in 1997 and also mandated in 1999 by the  "Third Generation Partnership Project" $\rm (3GPP)$  as the standard voice codec for third generation mobile systems such as UMTS.

• In contrast to conventional AMR,  where the voice signal is bandlimited to the frequency range from  $\text{300 Hz}$  to   $\text{3.4 kHz}$,  "'Wideband AMR",  which was developed and standardized for UMTS in 2007,  assumes a wideband signal   $\text{(50 Hz - 7 kHz)}$.  This is therefore also suitable for music signals.

⇒   You can visualize the quality of these voice coding schemes for speech and music with the  $($German language$)$  SWF applet 
               "Qualität verschiedener Sprach–Codecs"   ⇒   "Quality of different voice codecs".

GSM Fullrate Vocoder

LPC, LTP and RPE parameters in the GSM Full Rate Vocoder

Table of full rate codec parameters

In the  »Full Rate Vocoder«,  the analog speech signal in the frequency range between  $300 \ \rm Hz$  and  $3400 \ \rm Hz$ 

• is first sampled with  $8 \ \rm kHz$  and

• then linearly quantized with  $13$  bits   ⇒   »A/D conversion«,

resulting in a data rate of  $104 \ \rm kbit/s$.

In this method,  speech coding is performed in four steps:

1. The preprocessing,
2. the setting of the short-term analyze filter  $($Linear Predictive Coding,  $\rm LPC)$,
3. the control of the Long Term Prediction  $\rm (LTP)$  filter,  and
4. the encoding of the residual signal by a sequence of pulses  $($Regular Pulse Excitation,  $\rm RPE)$.

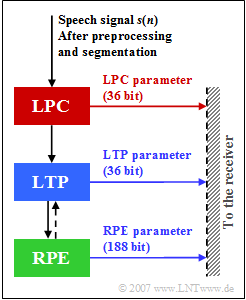
In the upper graph,  $s(n)$  denotes the speech signal sampled and quantized at distance  $T_{\rm A} = 125\ \rm µ s$  after the continuously performed preprocessing,  where

• the digitized microphone signal is freed from a possibly existing DC signal component  $($"offset"$)$  in order to avoid a disturbing whistling tone of approx.  $2.6 \ \rm kHz$  during decoding when recovering the higher frequency components,  and

• additionally,  higher spectral components of  $s(n)$  are raised to improve the computational accuracy and effectiveness of the subsequent LPC analysis.

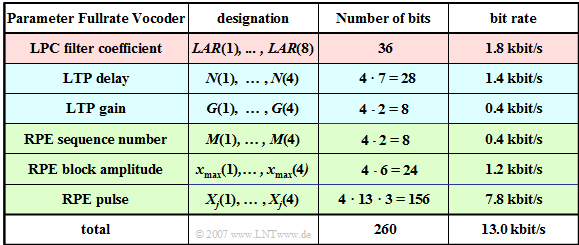
The table shows the  $76$  parameters  $(260$ bit$)$  of the functional units LPC, LTP and RPE.  The meaning of the individual quantities is described in detail on the following pages.

All processing steps  $($LPC, LTP, RPE$)$  are performed in blocks of  $20 \ \rm ms$  duration over  $160$  samples of the preprocessed speech signal,  which are called  »GSM speech frames« .

• In the full rate codec,  a total of  $260$ bits  are generated per voice frame,  resulting in a data rate of  $13 \rm kbit/s$.

• This corresponds to a compression of the speech signal by a factor  $8$  $(104 \ \rm kbit/s$  related to  $13 \ \rm kbit/s)$.

Linear Predictive Coding

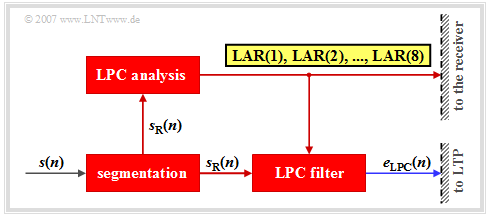
The block  «Linear Predictive Coding»  $\rm (LPC)$  performs short-time prediction, that is, it determines the statistical dependencies among the samples in a short range of one millisecond.  The following is a brief description of the LPC principle circuit:

Building blocks of GSM Linear Predictive Coding  $\rm (LPC)$

• First,  for this purpose  the time-unlimited signal  $s(n)$  is segmented into intervals  $s_{\rm R}(n)$  of  $20\ \rm ms$ duration  $(160$ samples$)$.  By convention,  the run variable within such a speech frame  $($German:  "Rahmen"   ⇒   subscript:  "R"$)$  can take the values  $n = 1$, ... , $160$.

• In the first step of  LPC analysis  dependencies between samples are quantified by the autocorrelation  $\rm ACF)$  coefficients with indices  $0 ≤ k ≤ 8$  :

$$φ_{\rm s}(k) = \text{E}\big [s_{\rm R}(n) · s_{\rm R}(n + k)\big ].$$

• From these nine ACF values,  using the so-called  "Schur recursion"  eight reflection coefficients  $r_{k}$  are calculated,  which serve as a basis for setting the coefficients of the LPC analysis filter for the current frame.

• The coefficients  $r_{k}$  have values between  $±1$.  Even small changes in  $r_{k}$  at the edge of their value range cause large changes for speech coding.  The eight reflectance values  $r_{k}$  are represented logarithmically   ⇒   LAR parameters  $($"Log Area Ratio"$)$:

$${\rm LAR}(k) = \ln \ \frac{1-r_k}{1+r_k}, \hspace{1cm} k = 1,\hspace{0.05cm} \text{...}\hspace{0.05cm} , 8.$$

• Then,  the eight LAR parameters are quantized by different bit numbers according to their subjective meaning,  encoded and made available for transmission. 

• The first two parameters are represented with six bits each, 
• the next two with five bits each, 
• $\rm LAR(5)$  and  $\rm LAR(6)$  with four bits each,  and
• the last two –   $\rm LAR(7)$  and  $\rm LAR(8)$–   with three bits each.

• If the transmission is error-free,  the original speech signal  $s(n)$  can be completely reconstructed again at the receiver from the eight LPC parameters  $($in total  $36$  bits$)$  with the corresponding LPC synthesis filter,  if one disregards the unavoidable additional quantization errors due to the digital description of the LAR coefficients.

• Further,  the prediction error signal  $e_{\rm LPC}(n)$  is obtained using the LPC filter.  This is also the input signal for the subsequent long-term prediction.  The LPC filter is not recursive and has only a short memory of about one millisecond.

LPC Prediction error signal at GSM  $($time–frequency representation$)$. Korrektur speech signal

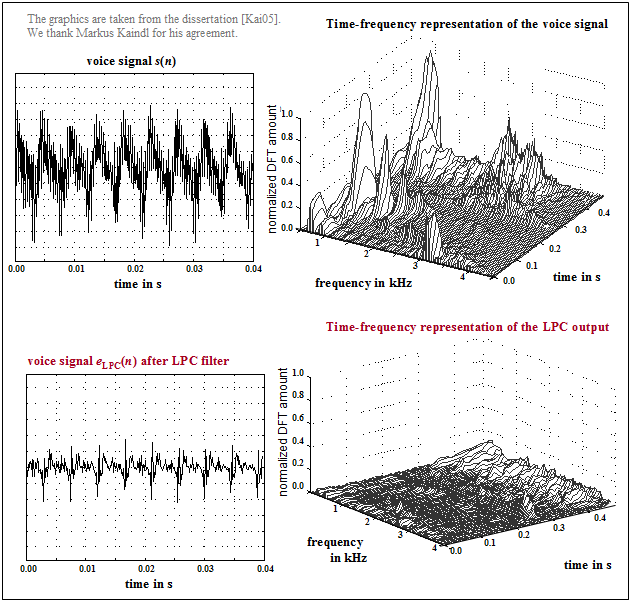
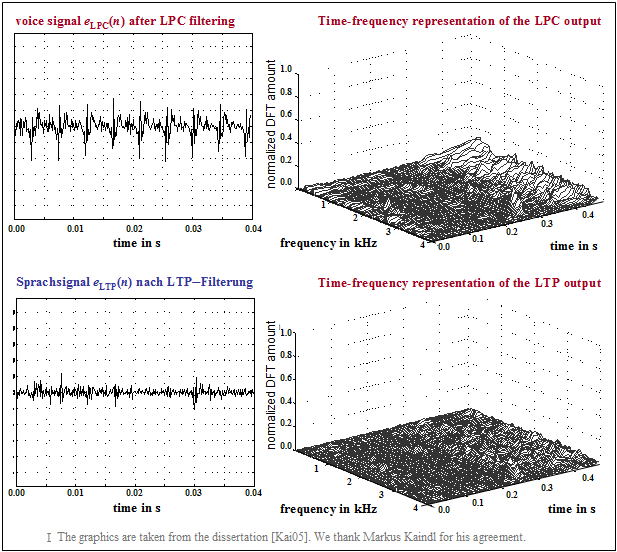
$\text{Example 1:}$  The graph from  [Kai05]  shows

• top left:  a section of the speech signal  $s(n)$, 

• top right:  its time-frequency representation,

• bottom left:  the LPC prediction error signal  $e_{\rm LPC}(n)$,

• bottom right:  its time-frequency representation,

One can see from these pictures

1. the smaller amplitude of  $e_{\rm LPC}(n)$  compared to  $s(n)$,
2. the significantly reduced dynamic range,  and
3. the flatter spectrum of the remaining signal.

Long Term Prediction

Long Term Prediction (LTP) exploits the property of the speech signal that it also has periodic structures (voiced sections). This fact is used to reduce the redundancy present in the signal.

Blocks of GSM Long Term Prediction (LTP)

• The long-term prediction (LTP analysis and filtering) is performed four times per speech frame, i.e. every  $5 \rm ms$ .
• The four subblocks consist of $40$ samples each and are identified by  $i = 1$, ... , $4$  numbered.

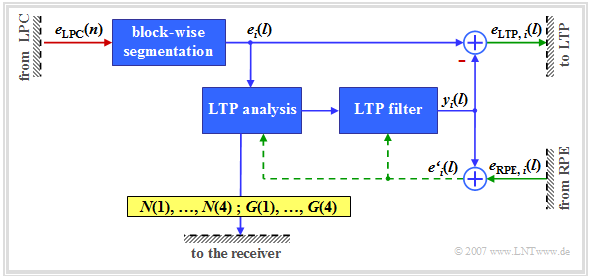
The following is a short description according to the above LTP–schematic diagram - see  [Kai05].

• The input signal is the output signal  $e_{\rm LPC}(n)$  of the short-term prediction. The signals after segmentation into four subblocks are denoted by  $e_i(l)$  where each  $l = 1, 2$, ... , $40$  holds.

• For this analysis, the cross-correlation function  $φ_{ee\hspace{0.03cm}',\hspace{0.05cm}i}(k)$  of the current subblock  $i$  of the LPC predictor error signal  $e_i(l)$  with the reconstructed LPC residual signal  $e\hspace{0.03cm}'_i(l)$  from the three previous subframes. The memory of this LTP predictor is between  $5 \ \rm ms$  and  $15 \ \rm ms$  and is thus significantly longer than that of the LPC predictor  $(1 \ \rm ms)$.
• $e\hspace{0.03cm}'_i(l)$  is the sum of the LTP filter output signal  $y_i(l)$  and the correction signal  $e_{\rm RPE,\hspace{0.05cm}i}(l)$ provided by the following component  (Regular Pulse Excitation)  for the  $i$-th subblock.
• The value of  $k$ for which the cross-correlation function  $φ_{ee\hspace{0.03cm}',\hspace{0.05cm}i}(k)$  becomes maximum determines the optimal LTP delay  $N(i)$ for each subblock  $i$ . The delays  $N(1)$  to  $N(4)$  are each quantised to seven bits and made available for transmission.
• The gain factor  $G(i)$  associated with  $N(i)$  - also called LTP gain  - is determined so that the subblock found at the location  $N(i)$  after multiplication by  $G(i)$  best matches the current subframe  $e_i(l)$ . The gains  $G(1)$  to  $G(4)$  are each quantised by two bits and together with  $N(1)$, ..., $N(4)$  give the  $36$  bits for the eight LTP parameters.
• The signal  $y_i(l)$  after LTP analysis and filtering is an estimated signal for the LPC signal  $e_i(l)$  in  $i$-th subblock. The difference between the two gives the LTP residual signal  $e_{\rm LTP,\hspace{0.05cm}i}(l)$, which is passed on to the next functional unit "RPE".

$\text{Example 2:}$  The graph from  [Kai05]  shows.

• above the LPC prediction error signal  $e_{\rm LPC}(n)$  - simultaneously the LTP input signal,
• below the residual error signal  $e_{\rm LTP}(n)$  after long-term prediction.

LTP–prediction error signal at GSM (time–frequency representation) correction'

Only one subblock is considered. Therefore, the same letter  $n$  is used here for the discrete time in LPC and LTP.

One can see from these representations

• the smaller amplitudes of  $e_{\rm LTP}(n)$  compared to  $e_{\rm LPC}(n)$  and
• the significantly reduced dynamic range of  $e_{\rm LTP}(n)$,
• especially in periodic, i.e. voiced, sections.

Also in the frequency domain, a reduction of the prediction error signal due to the long-term prediction is evident.

Regular Pulse Excitation – RPE Coding

Das Signal nach LPC– und LTP–Filterung ist bereits redundanz–reduziert, das heißt, es benötigt eine geringere Bitrate als das abgetastete Sprachsignal  $s(n)$.

Bausteine der Regular Pulse Excitation (RPE) bei GSM

• Nun wird in der nachfolgenden Funktionseinheit  Regular Pulse Excitation  (RPE) die Irrelevanz weiter verringert.
• Das bedeutet:   Signalanteile, die für den subjektiven Höreindruck weniger wichtig sind, werden entfernt.

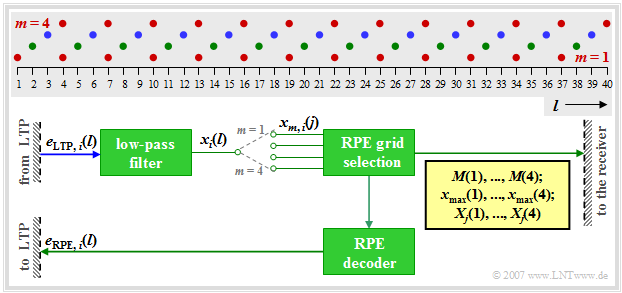
Zu diesem Blockschaltbild ist anzumerken:

• Die RPE–Codierung wird jeweils für  $5 \ \rm ms$–Teilrahmen  $(40$ Abtastwerte$)$  durchgeführt. Dies ist hier durch den Index  $i$  im Eingangssignal  $e_{\rm LTP},\hspace{0.03cm} i(l)$  angedeutet, wobei mit  $i = 1, 2, 3, 4$  wieder die einzelnen Subblöcke durchnummeriert sind.
• Im ersten Schritt wird das LTP–Prädiktionsfehlersignal  $e_{{\rm LTP}, \hspace{0.03cm}i}(l)$  durch ein Tiefpassfilter auf etwa ein Drittel der ursprünglichen Bandbreite – also auf  $1.3 \ \rm kHz$  – bandbegrenzt. Dies ermöglicht in einem zweiten Schritt eine Reduktion der Abtastrate um ca. den Faktor  $3$.
• So wird das Ausgangssignal  $x_i(l)$  mit  $l = 1$, ... , $40$  durch Unterabtastung in vier Teilfolgen  $x_{m, \hspace{0.03cm} i}(j)$  mit  $m = 1$, ... , $4$  und  $j = 1$, ... , $13$  zerlegt. Diese Aufspaltung ist in der Grafik verdeutlicht.
• Die Teilfolgen  $x_{m,\hspace{0.03cm} i}(j)$  beinhalten folgende Abtastwerte des Signals  $x_i(l)$:
  • $m = 1$:   $l = 1, \ 4, \ 7$, ... , $34, \ 37$ (rote Punkte),
  • $m = 2$:   $l = 2, \ 5, \ 8$, ... , $35, \ 38$ (grüne Punkte),
  • $m = 3$:   $l = 3, \ 6, \ 9$, ... , $36, \ 39$ (blaue Punkte),
  • $m = 4$:   $l = 4, \ 7, \ 10$, ... , $37, \ 40$ $($ebenfalls rot, weitgehend identisch mit  $m = 1)$.

• Für jeden Subblock  $i$  wird im Block  RPE Grid Selection  die Teilfolge  $x_{m,\hspace{0.03cm}i}(j)$  mit der höchsten Energie ausgewählt und der Index  $M_i$  der  optimalen Folge  mit zwei Bit quantisiert und als  $\mathbf{M}(i)$   übertragen. Insgesamt benötigen die vier RPE–Teilfolgen–Indizes  $\mathbf{M}(1)$, ... ,  $\mathbf{M}(4)$  somit acht Bit.
• Von der optimalen Teilfolge für den Subblock  $i$  $($mit Index  $M_i)$  wird das  Betragsmaximum  $x_{\rm max,\hspace{0.03cm}i}$  ermittelt, dieser Wert mit sechs Bit logarithmisch quantisiert und als  $\mathbf{x_{\rm max}}(i)$  zur Übertragung bereit gestellt. Insgesamt benötigen die vier RPE–Blockamplituden  $24$  Bit.
• Zusätzlich wird für jeden Subblock  $i$  die optimale Teilfolge auf  $x_{{\rm max},\hspace{0.03cm}i}$  normiert. Die so erhaltenen  $13$  Abtastwerte werden anschließend mit jeweils drei Bit quantisiert und als  $\mathbf{X}_j(i)$  codiert übertragen. Die  $4 · 13 · 3 = 156$  Bit beschreiben den so genannten  RPE–Pulse.
• Anschließend werden diese RPE–Parameter lokal wieder decodiert und als Signal  $e_{{\rm RPE},\hspace{0.03cm}i}(l)$  an das LTP–Synthesefilter im vorherigen Subblock zurückgeführt, woraus zusammen mit dem LTP–Schätzsignal  $y_i(l)$  das Signal  $e\hspace{0.03cm}'_i(l)$  erzeugt wird (siehe  LTP–Grafik).
• Durch das Zwischenfügen von jeweils zwei Nullwerten zwischen zwei übertragenen RPE–Abtastwerten wird näherungsweise das Basisband von Null bis  $1300 \ \rm Hz$  in den Bereich von  $1300 \ \rm Hz$  bis  $2600 \ \rm Hz$  in Kehrlage und von  $2600 \ \rm Hz$  bis  $3900 \ \rm Hz$  in Normallage gefaltet. Dies ist der Grund für die notwendige Gleichsignalbefreiung in der Vorverarbeitung. Sonst entstünde durch die beschriebene Faltungsoperation ein störender Pfeifton bei  $2.6 \ \rm kHz$.

Halfrate Vocoder und Enhanced Fullrate Codec

Nach der Standardisierung des Vollraten–Codecs im Jahre 1991 ging es in der Folgezeit um die Entwicklung neuer Sprachcodecs mit zwei spezifischen Zielen, nämlich um

• die bessere Ausnutzung der in GSM–Systemen verfügbaren Bandbreite, und
• die Verbesserung der Sprachqualität.

Diese Entwicklung kann wie folgt zusammengefasst werden:

• Bis 1994 wurde mit dem  Halfrate Vocoder  (deutsch:  Halbraten-Codec)  ein neues Verfahren entwickelt. Dieser hat eine Datenrate von  $5.6 \ \rm kbit/s$  und bietet so die Möglichkeit, Sprache in einem halben Verkehrskanal bei annähernd gleicher Qualität zu übertragen. Dadurch können auf einem Zeitschlitz zwei Gespräche gleichzeitig abgewickelt werden. Der Halbraten–Codec wurde allerdings von den Mobilfunkbetreibern nur dann eingesetzt, wenn eine Funkzelle überlastet war. Inzwischen spielt der Halfrate–Codec keine Rolle mehr.
• Um die Sprachqualität weiter zu verbessern, wurde 1995 der  Enhanced Fullrate Codec  (EFR–Codec) eingeführt. Dieses Sprachcodierverfahren – ursprünglich für das US–amerikanische DCS1900–Netz entwickelt – ist ein Vollraten–Codec mit der (etwas niedrigeren) Datenrate  $12.2 \ \rm kbit/s$. Die Nutzung dieses Codecs muss natürlich vom Mobiltelefon unterstützt werden.
• Statt der RPE–LTP–Komprimierung (Regular Pulse Excitation – Long Term Prediction) beim herkömmlichen Vollraten–Codec wird bei dieser Weiterentwicklung zudem  Algebraic Code Excitation Linear Prediction  (ACELP) angewandt, was eine deutlich bessere Sprachqualität und eine ebenfalls verbesserte Fehlererkennung und –verschleierung bietet. Nähere Informationen darüber finden Sie auf der übernächsten Seite.

Adaptive Multi–Rate Codec

Die bisher beschriebenen GSM–Codecs arbeiten hinsichtlich Sprach– und Kanalcodierung unabhängig von den Kanalbedingungen und der Netzauslastung stets mit einer festen Datenrate. 1997 wurde ein neues adaptives Sprachcodierverfahren für Mobilfunksysteme entwickelt und kurz darauf durch das European Telecommunications Standards Institute (ETSI) nach Vorschlägen der Firmen Ericsson, Nokia und Siemens standardisiert. Bei den Forschungsarbeiten zum Systemvorschlag der Siemens AG war der Lehrstuhl für Nachrichtentechnik der TU München, der dieses Lerntutorial $\rm LNTwww$ zur Verfügung stellt, entscheidend beteiligt. Näheres finden Sie unter  [Hin02].

Der  Adaptive Multi–Rate Codec  – abgekürzt AMR – hat folgende Eigenschaften:

• Er passt sich flexibel an die aktuellen Kanalgegebenheiten und an die Netzauslastung an, indem er entweder im Vollraten–Modus (höhere Sprachqualität) oder im Halbraten–Modus (geringere Datenrate) arbeitet. Daneben gibt es noch etliche Zwischenstufen.
• Er bietet sowohl beim Vollraten– als auch beim Halbratenverkehrskanal eine verbesserte Sprachqualität, was auf die flexibel handhabbare Aufteilung der zur Verfügung stehenden Brutto–Kanaldatenrate zwischen Sprach– und Kanalcodierung zurückzuführen ist.
• Er besitzt eine größere Robustheit gegenüber Kanalfehlern als die Codecs aus der Frühzeit der Mobilfunktechnik. Dies gilt besonders beim Einsatz im Vollraten–Verkehrskanal.

Der AMR–Codec stellt  acht verschiedene Modi  mit Datenraten zwischen  $12.2 \ \rm kbit/s$  $(244$  Bit pro Rahmen von  $20 \ \rm ms)$  und  $4.75 \ \rm kbit/s$  $(95$ Bit pro Rahmen$)$ zur Verfügung. Drei Modi spielen eine herausgehobene Rolle, nämlich

• $12.2 \ \rm kbit/s$  – der verbesserte GSM–Vollraten–Codec (EFR-Codec),
• $7.4 \ \rm kbit/s$  – die Sprachkompression gemäß dem US–amerikanischen Standard IS–641, und
• $6.7 \ \rm kbit/s$  – die EFR–Sprachübertragung des japanischen PDC–Mobilfunkstandards.

Die folgenden Beschreibungen beziehen sich meist auf den Modus mit  $12.2 \ \rm kbit/s$.

Zusammenstellung der AMR–Parameter

• Alle Vorgänger–Verfahren des AMR basieren auf der Minimierung des Prädiktionsfehlersignals durch eine Vorwärtsprädiktion in den Teilschritten LPC, LTP und RPE.
• Im Gegensatz dazu verwendet der AMR-Codec eine Rückwärtsprädiktion gemäß dem Prinzip „Analyse durch Synthese”. Dieses Codierungsprinzip bezeichnet man auch als  Algebraic Code Excited Linear Prediction  (ACELP).

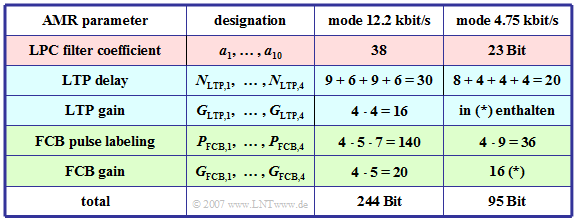
In der Tabelle sind die Parameter des Adaptive Multi–Rate Codecs für zwei Modi zusammengestellt:

•   $244$  Bit pro  $20 \ \rm ms$   ⇒   Modus  $12.2 \ \rm kbit/s$,
•   $95$  Bit pro  $20 \ \rm ms$   ⇒   Modus  $4.75 \ \rm kbit/s$.

Algebraic Code Excited Linear Prediction

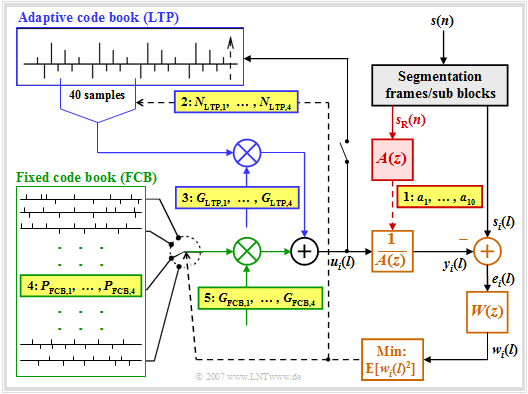
Die Grafik zeigt den auf  ACELP  basierenden  AMR-Codec. Es folgt eine kurze Beschreibung des Prinzips. Eine detaillierte Beschreibung finden Sie zum Beispiel in  .

Algebraic Code Excited Linear Prediction – Prinzip

• Das Sprachsignal  $s(n)$, wie beim GSM–Vollraten–Sprachcodec mit  $8 \ \rm kHz$  abgetastet und mit  $13$  Bit quantisiert, wird vor der weiteren Verarbeitung in Rahmen  $s_{\rm R}(n)$  mit  $n = 1$, ... , $160$  bzw. in Subblöcke  $s_i(l)$  mit  $i = 1, 2, 3, 4$  und  $l = 1$, ... , $40$  segmentiert.
• Die Berechnung der LPC–Koeffizienten erfolgt im rot hinterlegten Block rahmenweise alle  $20 \ \rm ms$  entsprechend  $160$  Abtastwerten, da innerhalb dieser kurzen Zeitspanne die spektrale Einhüllende des Sprachsignal  $s_{\rm R}(n)$  als konstant angesehen werden kann.
• Zur LPC–Analyse wird meist ein Filter  $A(z)$  der Ordnung  $10$  gewählt. Beim höchstratigen Modus mit  $12.2 \ \rm kbit/s$  werden die aktuellen Koeffizienten  $a_k \ ( k = 1$, ... , $10)$  der Kurzzeitprädiktion alle  $10\ \rm ms$  quantisiert, codiert und beim gelb hinterlegten Punkt 1 zur Übertragung bereitgestellt.
• Die weiteren Schritte des AMR werden alle  $5 \ \rm ms$  entsprechend den  $40$  Abtastwerten der Signale  $s_i(l)$  durchgeführt. Die Langzeitprädiktion (LTP) – im Bild blau umrandet – ist hier als adaptives Codebuch realisiert, in dem die Abtastwerte der vorangegangenen Subblöcke eingetragen sind.
• Für die Langzeitprädiktion (LTP) wird zunächst die Verstärkung  $G_{\rm FCB}$  für das  Fixed Code Book  (FCB) zu Null gesetzt, so dass eine Folge von  $40$  Samples des adaptiven Codebuchs am Eingang  $u_i(l)$  des durch die LPC festgelegten Sprachtraktfilters  $A(z)^{–1}$  anliegen. Der Index  $i$  bezeichnet den betrachteten Subblock.
• Durch Variation der beiden LTP–Parameter  $N_{{\rm LTP},\hspace{0.05cm}i}$  und  $G_{{\rm LTP},\hspace{0.05cm}i}$  soll für diesen  $i$–ten Subblock erreicht werden, dass der quadratische Mittelwert – also die mittlere Leistung – des gewichteten Fehlersignals  $w_i(l)$  minimal wird.
• Das Fehlersignal  $w_i(l)$  ist gleich der Differenz zwischen dem aktuellen Sprachrahmen  $s_i(l)$  und dem Ausgangssignal  $y_i(l)$  des so genannten Sprachtraktfilters bei Anregung mit  $u_i(l)$, unter Berücksichtigung des Wichtungsfilters  $W(z)$  zur Anpassung an die Spektraleigenschaften des menschlichen Gehörs.
• In anderen Worten:   $W(z)$  entfernt solche spektralen Anteile im Signal  $e_i(l)$, die von einem „durchschnittlichen” Ohr nicht wahrgenommen werden. Beim Modus  $12.2 \ \rm kbit/s$  verwendet man  $W(z) = A(z/γ_1)/A(z/γ_2)$  mit konstanten Faktoren  $γ_1 = 0.9$  und  $γ_2 = 0.6$.
• Für jeden Subblock kennzeichnet  $N_{{\rm LTP},\hspace{0.05cm}i}$  die bestmögliche LTP–Verzögerung, die zusammen mit der LTP–Verstärkung  $G_{{\rm LTP},\hspace{0.05cm}i}$  nach Mittelung bezüglich  $l = 1$, ... , $40$  den quadratischen Fehler  $\text{E}[w_i(l)^2]$  minimiert. Gestrichelte Linien kennzeichnen Steuerleitungen zur iterativen Optimierung.
• Man bezeichnet die beschriebene Vorgehensweise als  Analyse durch Synthese. Nach einer ausreichend großen Anzahl an Iterationen wird der Subblock  $u_i(l)$  in das adaptive Codebuch aufgenommen. Die ermittelten LTP–Parameter  $N_{{\rm LTP},\hspace{0.05cm}i}$  und  $G_{{\rm LTP},\hspace{0.05cm}i}$  werden codiert und zur Übertragung bereitgestellt.

Fixed Code Book – FCB

Spureinteilung beim ACELP-Sprachcodec

Nach der Ermittlung der besten adaptiven Anregung erfolgt die Suche nach dem besten Eintrag im festen Codebuch (Fixed Code Book, FCB).

• Dieses liefert die wichtigste Information über das Sprachsignal.
• Zum Beispiel werden beim  $12.2 \ \rm kbit/s$–Modus hieraus pro Subblock  $40$  Bit abgeleitet.
• Somit gehen in jedem Rahmen von  $20$  Millisekunden  $160/244 ≈ 65\%$  der Codierung auf den im Bild auf der letzten Seite grün umrandeten Block zurück.

Das Prinzip lässt sich anhand der Grafik in wenigen Stichpunkten wie folgt beschreiben:

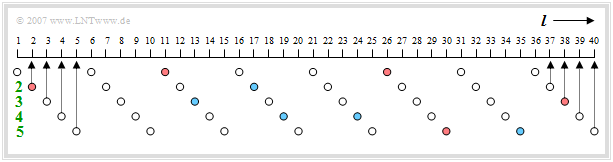
• Im festen Codebuch kennzeichnet jeder Eintrag einen Puls, bei dem genau  $10$  der  $40$  Positionen mit  $+1$  bzw.  $-1$  belegt sind. Erreicht wird dies gemäß der Grafik durch fünf Spuren mit jeweils acht Positionen, von denen genau zwei die Werte  $±1$  aufweisen und alle anderen Null sind.
• Ein roter Kreis in obiger Grafik  $($an den Positionen  $2,\ 11,\ 26,\ 30,\ 38)$  kennzeichnet eine  $+1$  und ein blauer eine  $-1$  $($im Beispiel bei  $13,\ 17,\ 19,\ 24,\ 35)$. In jeder Spur werden die beiden belegten Positionen mit lediglich je drei Bit codiert (da es nur acht mögliche Positionen gibt).
• Für das Vorzeichen wird ein weiteres Bit verwendet, welches das Vorzeichen des erstgenannten Impulses definiert. Ist die Pulsposition des zweiten Impulses größer als die des ersten, so hat der zweite Impuls das gleiche Vorzeichen wie der erste, ansonsten das entgegengesetzte.
• In der ersten Spur des obigen Beispiels gibt es positive Pulse auf Position  $2 \ (010)$  und Position  $5 \ (101)$, wobei die Positionszählung bei  $0$  beginnt. Diese Spur ist also gekennzeichnet durch die Positionen  $010$  und  $101$  sowie das Vorzeichen  $1$  (positiv).
• Die Kennzeichnung für die zweite Spur lautet:   Positionen  $011$  und  $000$, Vorzeichen  $0$. Da hier die Pulse an Position  $0$  und  $3$  unterschiedliche Vorzeichen haben, steht  $011$  vor  $000$. Das Vorzeichen $0$   ⇒   negativ bezieht sich auf den Puls an der erstgenannten Position  $3$.
• Ein jeder Puls – bestehend aus  $40$  Impulsen, von denen allerdings  $30$  das Gewicht "Null" besitzen – ergibt ein stochastisches, rauschähnliches Akustiksignal, das nach Verstärkung mit  $G_{{\rm LTP},\hspace{0.05cm}i}$  und Formung durch das LPC–Sprachtraktfilter  $A(z)^{–1}$  den Sprachrahmen  $s_i(l)$  approximiert.

Aufgaben zum Kapitel

Aufgabe 3.5: GSM–Vollraten–Sprachcodec

Aufgabe 3.6: Adaptive Multi–Rate Codec