Double-Sideband Amplitude Modulation

Beschreibung im Frequenzbereich (1)

Wir betrachten die folgende Aufgabenstellung: Ein Nachrichtensignal $q(t)$ , dessen Spektrum $Q(f)$ auf den Bereich $\pm B_{\rm NF}$ bandbegrenzt ist, soll mit Hilfe einer harmonischen Schwingung der Frequenz $f_{\rm T}$ , die wir im Weiteren als Trägersignal $z(t)$ bezeichnen, in einen höherfrequenten Bereich verschoben werden, in dem der Kanalfrequenzgang $H_{\rm K}(f)$ günstige Eigenschaften aufweist.

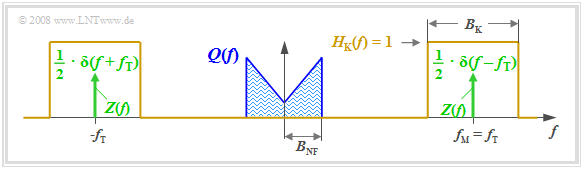
Darstellung der Amplitudenmodulation im Frequenzbereich

Die Grafik verdeutlicht die Aufgabenstellung, wobei folgende vereinfachende Annahmen getroffen sind:

Das gezeichnete Spektrum $Q(f)$ ist hier schematisch zu verstehen. Es besagt, dass in $q(t)$ nur Spektralanteile im Bereich $|f| ≤ B_{\rm NF}$ enthalten sind. $Q(f)$ könnte auch ein Linienspektrum sein.
Der Kanal sei in einem Bereich der Bandbreite $B_{\rm K}$ um die Frequenz $f_{\rm M}$ ideal, das heißt, es gelte $H_{\rm K}(f) =$ 1 für $|f – f_{\rm M}| ≤ B_{\rm K}/2.$ Rauschstörungen werden vorerst nicht betrachtet.
Das Trägersignal sei cosinusförmig (Phase $ϕ_T =$ 0) und besitze die Amplitude $A_{\rm T} =$ 1 (ohne Einheit). Die Trägerfrequenz $f_{\rm T}$ sei gleich der Mittenfrequenz des Übertragungsbandes.
Das Spektrum des Trägersignals $z(t) = \cos(ω_{\rm T} · t)$ lautet somit (in der Grafik grün eingezeichnet):

$Z(f) = \frac{1}{2} \cdot \delta (f + f_{\rm T})+\frac{1}{2} \cdot \delta (f - f_{\rm T})\hspace{0.05cm}.$