Funktionsweise bei idealen Bedingungen
Wir gehen zunächst von folgenden Voraussetzungen aus:
- Das Quellensignal $q(t)$ sei gleichsignalfrei und betragsmäßig auf $q_{\rm max}$ begrenzt.
- Die Übertragung basiert auf dem Modulationsverfahren „ZSB–AM mit Träger”. Zur einfacheren Darstellung wird die Trägerphase ohne Einschränkung der Allgemeingültigkeit $\mathbf{ϕ_{\rm T} } =$ 0 gesetzt:
$$s(t) = \left(q(t) + A_{\rm T}\right) \cdot \cos (\omega_{\rm T}\cdot t )\hspace{0.05cm}.$$
- Der Modulationsgrad sei $m$ ≤ 1. Aus der Definition $m = q_{\rm max}/A_{\rm T}$ folgt somit auch $q(t) + A_{\rm T}$ ≥ 0.
- Der Kanal sei ideal, das heißt, es gibt keine Verzerrungen, keine Dämpfung, keine Laufzeit und keine (Rausch–) Störungen. Mit $H_{\rm K}(f) =$ 1 und $n(t) =$ 0 erhält man somit für das Empfangssignal:
$$r(t) = s(t) = a(t) \cdot \cos (\omega_{\rm T}\cdot t )\hspace{0.05cm}.$$
- In dieser Gleichung bezeichnet $a(t)$ die Hüllkurve von $r(t)$. Die Phasenfunktion $\mathbf{ϕ}(t)$ ist 0.
Ein Hüllkurvendemodulator detektiert die Hüllkurve $a(t)$ seines Eingangssignals $r(t)$ und gibt diese nach Eliminierung des Gleichanteils $A_{\rm T}$ als Sinkensignal aus: $$v(t) = a(t) - A_{\rm T}\hspace{0.05cm}.$$ Die Entfernung des Gleichanteils $A_{\rm T}$ kann beispielsweise durch einen Hochpass realisiert werden, der alle Frequenzen bis auf $f =$ 0 ungehindert passieren lässt.
Sind alle obigen Voraussetzungen erfüllt, so gilt $υ(t) = q(t)$. Das bedeutet, dass mit einem (idealen) Hüllkurvendemodulator durchaus ein ideales Nachrichtenübertragungssystem realisiert werden kann.
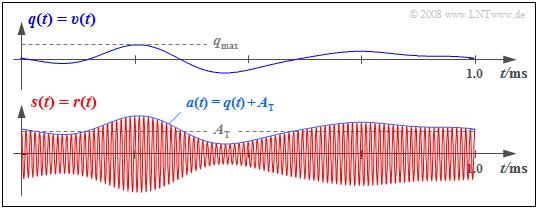
Unten sehen Sie das Empfangssignal $r(t) = s(t)$, wobei „ZSB–AM mit Träger” zugrunde liegt (Modulationsgrad $m =$ 0.5). Die vom Hüllkurvendemodulator auszuwertende Hüllkurve $a(t)$ ist gleich der Summe aus dem Quellensignal $q(t)$ und dem beim Sender zugesetzten Gleichanteil $A_{\rm T}$.
Für das Demodulatorausgangssignal nach Eliminierung des Gleichanteils $A_{\rm T}$ mit einem Hochpass gilt $υ(t) = q(t)$, vorausgesetzt, dass das Quellensignal $q(t)$ keinen Gleichanteil beinhaltet hat. Ein solcher würde durch den Hochpass ebenfalls entfernt.