Erstes Nyquistkriterium im Zeitbereich
Für dieses Kapitel wurde vorausgesetzt, dass die Detektion eines Symbols nicht durch Nachbarimpulse beeinträchtigt werden soll. Dies erreicht man durch die Detektion des Signals
\(d(t) = \sum \limits_{\it (\nu)} a_\nu \cdot g_d ( t - \nu T)\)
zu den Zeitpunkten νT immer dann, wenn der Detektionsgrundimpuls gd(t)
- auf den Bereich | t | < T beschränkt ist, was für das Kapitel 1.2 vorausgesetzt wurde, oder
- äquidistante Nulldurchgänge zu den Zeitpunkten νT aufweist.
Aus Gründen einer möglichst einfachen Darstellung wird im Kapitel 1.3 das Detektionsstörsignal dN(t) als vernachlässigbar klein angenommen.
- \[g_d ( t = \nu T)= 0 \hspace{0.3cm}{\rm{f\ddot{u}r}}\hspace{0.3cm} \nu = \pm 1, \pm 2,\pm 3,\hspace{0.05cm}...\]
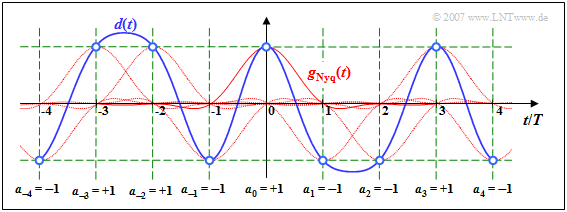
Zu den Detektionszeitpunkten gilt d(νT) = aν · gNyq(0), wie aus den blauen Kreisen und dem grünen Raster hervorgeht. Die Nachläufer der vorangegangenen Impulse (ν < 0) sowie die Vorläufer der nachfolgenden Impulse (ν > 0) beeinflussen beim Nyquistsystem die Detektion des Symbols a0 nicht.
Der Vollständigkeit halber sei erwähnt, dass für diese Grafik der Detektionsgrundimpuls
\(g_{\rm Nyq} ( t )= g_0 \cdot {\rm si} \left ( \frac{\pi \cdot
t}{T}\right)\cdot {\rm si} \left ( \frac{\pi \cdot t}{2 \cdot
T}\right)\)