Viterbi Receiver

1. Digital Signal Transmission
2. Impulsinterferenzen und Entzerrungsverfahren
3. Viterbi Receiver

• Previous page
• Next page

• Previous page
• Next page

Blockschaltbild und Voraussetzungen für Kapitel 3.8 (1)

Der Korrelationsempfänger ist im Sinne der Maximum–Likelihood–Entscheidungsregel optimal, das heißt, er führt bei gleichwahrscheinlichen Quellensymbolen zur minimalen Fehlerwahrscheinlichkeit. Nachteilig ist:

• Der Realisierungsaufwand steigt exponentiell mit der Länge N der zu detektierenden Symbolfolge.
  
• Da die Folge gemeinsam entschieden wird, kommt es bei großem N zu langen Verzögerungen.
  
  

In den 1970er Jahren hat Andrew J. Viterbi einen ML–Empfänger vorgeschlagen, der die Detektion von Teilen der empfangenen Nachricht erlaubt und bei dem sich der Realisierungsaufwand auch bei unendlich langen Folgen in Grenzen hält.

Zu den einzelnen Komponenten des Blockschaltbildes ist anzumerken:

• Das an den Empfangsgrundimpuls und die Störung angepasste Matched–Filter H_MF(f) dient der Störleistungsbegrenzung. Das MF–Ausgangssignal m(t) bzw. die Folge 〈m_ν〉 der äquidistanten Signalwerte nach der Abtastung besitzt das bestmögliche Signal–zu–Stör–Leistungsverhältnis.
  

• Aufgabe des Dekorrelationsfilters H_DF(f) ist es, aus der Folge 〈m_ν〉 die Detektionsabtastwerte d_ν = d_Sν + d_Nν zu gewinnen, deren Störanteile d_Nν unkorreliert sind. Dieses Filter wird deshalb auch Whitening–Filter genannt.
  

• Der Viterbi–Entscheider, der im Mittelpunkt der folgenden Betrachtungen steht, gewinnt aus der Folge 〈d_ν〉 seiner wertkontinuierlichen Eingangswerte die binäre Ausgangsfolge 〈υ_ν〉 entsprechend der Maximum–Likelihood–Regel mit der kleinstmöglichen Fehlerwahrscheinlichkeit Pr(υ_ν ≠ q_ν).
  
  

Die Beschreibung wird auf der nächsten Seite fortgesetzt.

Blockschaltbild und Voraussetzungen für Kapitel 3.8 (2)

Um den Viterbi–Algorithmus möglichst einfach beschreiben und veranschaulichen zu können, werden hier einige vereinfachende Voraussetzungen getroffen:

• Die Amplitudenkoeffizienten seien unipolar  ⇒  a_ν ∈ {0, 1}. Anzumerken ist, dass es bei der Verwendung bipolarer Koeffizienten a_ν ∈ {–1, +1} nur weniger Modifikationen bedarf.
  

• Der Grundimpuls g_d(t) besteht nur aus dem Hauptwert g₀ = g_d(t = T_D) und einem Vorläufer g_–1 = g_d(t = T_D – T).
  

• Damit ergeben sich für die wertkontinuierlichen Detektionsabtastwerte

\[d_{\nu} = a_{\nu}\cdot g_{0} + a_{\nu+1}\cdot g_{-1}+d_{{\rm N}\nu} \hspace{0.05cm},\]

wobei die Rauschkomponente d_Nν als gaußverteilt angenommen wird (Streuung σ_d).

Bei bipolarer Signalisierung ist der Algorithmus nicht aufwändiger. Dagegen steigt der Rechenaufwand, wenn der Detektionsgrundimpuls breiter wird und mehr als nur einen Vorläufer g_–1 aufweist. Die Vernachlässigung von Nachläufern stellt keine grundlegende Einschränkung dar, weil jeder Impuls g_d(t) diese Bedingung durch geeignete Wahl des Detektionszeitpunktes T_D erfüllen kann. Anzumerken ist weiter, dass im Folgenden alle Signalwerte auf 1 normiert werden.

: In der Grafik sind die Detektionsnutzabtastwerte d_sν als (blaue) Kreuze eingetragen, wobei die zugehörigen Amplitudenkoeffizienten a₁ = 1, a₂ = 1, a₃ = 0, ... aus dem grün eingezeichneten Quellensignal q(t) abgelesen werden können. Die Grundimpulswerte sind in diesem Beispiel zu g₀ = 0.7 und g_–1 = 0.3 angenommen. Aus der Grafik ist weiter zu erkennen, dass d_Sν nur vier verschiedene Werte, nämlich 0, g₀, g_–1 und

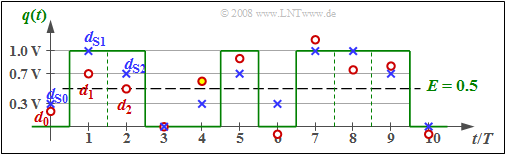
g₀ + g_–1, annehmen kann.

Die am Viterbi–Entscheider anstehenden Abtastwerte (rote Punkte) sind d₀ = 0.2, d₁ = 0.7, d₂ = 0.5, d₃ = 0, ... , wobei die Differenzen d_Nν = d_ν – d_Sν von einer AWGN–Rauschquelle herrühren.

Ein Schwellenwertentscheider (mit der Schwelle bei E = 0.5) würde bei diesen dargestellten zehn Bit mindestens eine Fehlentscheidung treffen (bei ν = 4), und eventuell eine weitere bei ν = 2, falls d₂ geringfügig kleiner ist als der Schwellenwert E = 0.5. Dagegen wird der Viterbi–Empfänger diese Folge der Länge 10 richtig entscheiden, wie auf den nächsten Seiten gezeigt werden wird.

Fehlergrößen und Gesamtfehlergrößen (1)

Wie in Kapitel 3.7 gibt Q ∈ {Q_i} die begrenzte, aus N Binärsymbolen bestehende Quellensymbolfolge an. Die Anzahl der möglichen Symbolfolgen Q_i ist somit 2^N. V bezeichnet wieder die Sinkensymbolfolge der Länge N, die vom Viterbi–Entscheider gleich der wahrscheinlichsten Folge Q_j gesetzt wird.

: Definition: Die Fehlergröße bezeichnet die quadratische Abweichung zwischen dem tatsächlichen, verrauschten Abtastwert d_ν und dem zur Folge Q_i gehörenden Nutzabtastwert d_Sν(i):

\[\varepsilon_{\nu}(i) = |d_{\nu} - d_{{\rm S}\nu}(i)|^2 \hspace{0.05cm}.\]

Die Gesamtfehlergröße γ_ν(i) kennzeichnet die Summe aller Fehlergrößen bis zum Zeitpunkt ν:

\[\gamma_{\nu}(i)= \sum_{k=0}^{\nu}\varepsilon_{k}(i) \hspace{0.05cm}.\]

Man bezeichnet γ_ν(i) auch als Metrik. Anzumerken ist, dass diese Definitionen an einem Grundimpuls mit Hauptwert g₀ und nur einem Vorläufer g_–1 angepasst sind. Bei υ Vorläufern müsste die obige Summe bei k = 1 – υ beginnen. Der Parameter i ∈ {0, ... , 2^N+1–1} wird meist binär dargestellt, so dass i gleichzeitig die Amplitudenkoeffizienten a₁, ... , a_ν+1 (jeweils entweder 0 oder 1) angibt.

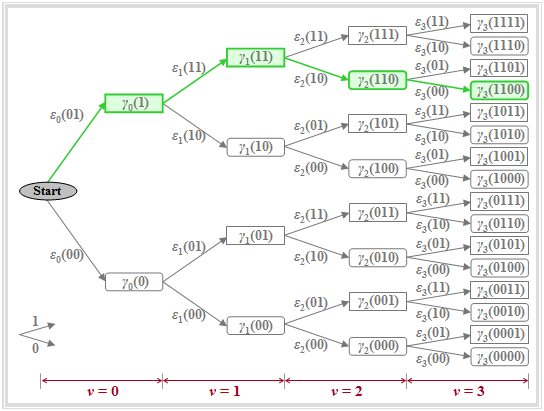
Die Grafik verdeutlicht die oben definierten Größen in einer Baumstruktur, woraus zu erkennen ist, dass die Gesamtfehlergrößen iterativ berechnet werden können:

\[\gamma_{\nu}(i)= \gamma_{\nu-1}(i')+\varepsilon_{k}(i'') \hspace{0.05cm}.\]

i, i' und i sind unterschiedliche Laufvariable. Die Bildbeschreibung folgt auf der nächsten Seite.

Fehlergrößen und Gesamtfehlergrößen (2)

Zu dieser Grafik, die hier nochmals eingeblendet werden kann, ist Folgendes anzumerken:

• Die Knoten des Baumdiagramms stehen für die Gesamtfehlergrößen γ_ν(i); deren Anzahl wird mit jedem Iterationsschritt verdoppelt. Zum Zeitpunkt ν gibt es 2^ν+1 solcher Knoten. Beispielsweise sind für ν = 3 genau 2⁴ = 16 Knoten zu erkennen.
  

• Die zu den Gesamtfehlergrößen γ_ν(i) gehörigen Amplitudenkoeffizienten ergeben sich, wenn man den Weg vom Anfangsknoten bis zum betrachteten Knoten verfolgt. Es wird vereinbart, dass einem nach oben gerichteten Zweig der Amplitudenkoeffizient 1 und einem nach unten gerichteten Zweig eine 0 zugeordnet wird.
  

• Beispielsweise kennzeichnet der grün hinterlegte Knoten γ₃(1100) die Gesamtfehlergröße unter der hypothetischen Annahme, dass die Symbole a₁ = 1, a₂ = 1, a₃ = 0, a₄ = 0 gesendet wurden. Diese Zuordnung kann auch aus den Richtungen der Pfeile im Baumdiagramm abgelesen werden: zunächst zweimal nach oben, dann zweimal nach unten.
  

• Aufgrund des Vorläufers muss bereits zum Zeitpunkt ν = 3 der Koeffizient a₄ mitberücksichtigt werden. Alle Knoten γ_ν(i), die unter der Voraussetzung a_ν+1 = 1 berechnet werden, sind im Baumdiagramm durch Rechtecke dargestellt, während die Hypothese a_ν+1 = 0 jeweils durch ein abgerundetes Rechteck symbolisiert ist, z. B. γ₂ (110) oder γ₃ (1100).
  

• Die Zweige im Baumdiagramm sind den Fehlergrößen ε_ν(i) zugeordnet. Beim vorausgesetzten Grundimpuls (nur g₀ und g_–1 sind ungleich 0) gibt es zu jedem Zeitpunkt mit Ausnahme des Startzustandes (ν = 0) genau vier unterschiedliche Größen:

\[\varepsilon_{\nu}(00) = |d_{\nu}|^2\hspace{0.05cm},\hspace{0.5cm}\varepsilon_{\nu}(01) = |d_{\nu}-g_{-1}|^2\hspace{0.05cm},\]

\[\varepsilon_{\nu}(10) = |d_{\nu}-g_{0}|^2\hspace{0.05cm},\hspace{0.2cm}\varepsilon_{\nu}(11) = |d_{\nu}-g_{0}-g_{-1}|^2\hspace{0.05cm}.\]

• Die Gesamtfehlergröße γ_ν ist gleich der Summe aus dem vorausgegangenen Knoten γ_ν–1 und dem dazwischenliegenden Zweig ε_ν. Beispielsweise gilt für die hervorgehobenen Knoten:

\[\gamma_{1}(11)=\gamma_{0}(1)+\varepsilon_{1}(11) ,\hspace{0.05cm} \gamma_{2}(110)=\gamma_{1}(11)+\varepsilon_{2}(10) ,\hspace{0.05cm} \gamma_{3}(1100)=\gamma_{2}(110)+\varepsilon_{3}(00) .\]

• Bei den ersten Knoten γ₀(0) und γ₀(1) wird berücksichtigt, dass vor der eigentlichen Übertragung (a₁, a₂, ...) vereinbarungsgemäß stets das Symbol a₀ = 0 übertragen wird. Daraus folgt:

\[\gamma_{0}(0)=\varepsilon_{0}(00)= |d_{0}|^2 \hspace{0.05cm},\hspace{0.2cm} \gamma_{0}(1)=\varepsilon_{0}(01)=|d_{0}-g_{-1}|^2 \hspace{0.05cm}.\]

Das nachfolgende Beispiel wird hoffentlich diese etwas ermüdenden Aussagen verdeutlichen.

Fehlergrößen und Gesamtfehlergrößen (3)

: Wir betrachten wie im letzten Beispiel die unipolare Quellensymbolfolge der Länge N = 3, mit den Amplitudenkoeffizienten a₁ = 1, a₂ = 1, a₃ = 0 und die weiteren Parameterwerte

\[g_{0}=0.7 \hspace{0.05cm},\hspace{0.2cm} g_{-1}=0.3 \hspace{0.05cm},\hspace{0.2cm} d_{0}=0.2 \hspace{0.05cm},\hspace{0.2cm} d_{1}=0.7 \hspace{0.05cm},\hspace{0.2cm} d_{2}=0.5 \hspace{0.05cm},\hspace{0.2cm} d_{3}=0 \hspace{0.05cm} \hspace{0.05cm}.\]

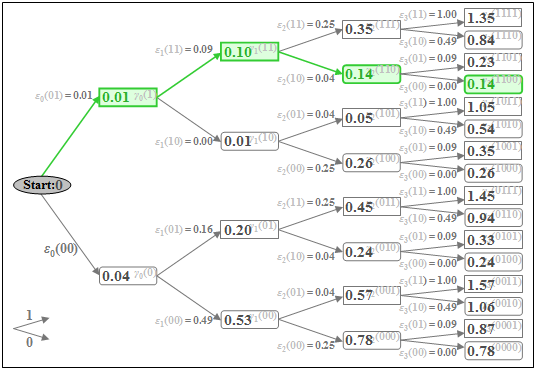
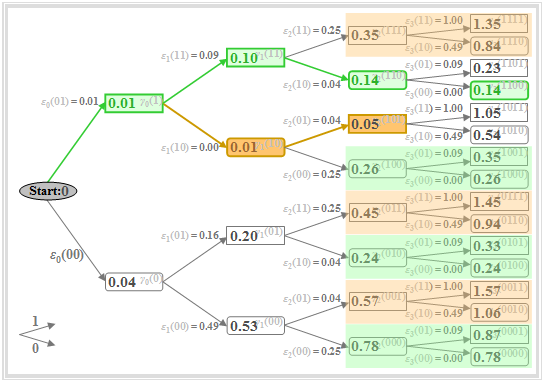
Nachfolgend ist das Baumdiagramm mit den Knoten γ_ν(i) für die Zeitpunkte ν = 0 bis ν = 3 dargestellt. Die Berechnung der sich ergebenden Fehlergrößen ε_ν(i) folgt auf der nächsten Seite.

Die minimale Gesamtfehlergröße γ₃(1100) ist gleich 0.14. Daraus ergeben sich die Koeffizienten der nach den vorliegenden Signalwerten d₀, d₁, d₂, d₃ mit größter Wahrscheinlichkeit gesendeten Folge zu a₁ = 1, a₂ = 1 und a₃ = 0 (grün eingezeichneter Pfad). Weiter ist zu sagen:

• Ist die Folgenlänge N = 3 (das heißt: nur drei Symbole werden durch den Viterbi–Empfänger gemeinsam entschieden), so ist auch die Entscheidung a₄ = 0 mit Sicherheit die richtige, da alle Koeffizienten a_ν>3 als 0 vorausgesetzt wurden.
  

• Bei längerer Folge (N > 3) kann aus dem minimalen Wert γ₃(1100) nicht unbedingt geschlossen werden, dass a₁ = 1, a₂ = 1, a₃ = 0 Teil der wahrscheinlichsten Folge ist. Bei Berücksichtigung weiterer Abtastwerte (d₄, d₅, ...) könnte sich dieses vorläufige Ergebnis durchaus noch ändern.
  
  

Die Berechnung der Fehlergrößen für ν = 0 bis ν = 3 wird auf der nächsten Zeile gezeigt.

Nachzutragen ist die Berechnung der Fehlergrößen für die Zeitpunkte ν = 0 bis ν = 3. Die unipolare Quellensymbolfolge hat die Länge N = 3. Die Amplitudenkoeffizienten seien a₁ = 1, a₂ = 1, a₃ = 0. Weiterhin gilt:

\[g_{0}=0.7 \hspace{0.05cm},\hspace{0.2cm} g_{-1}=0.3 \hspace{0.05cm},\hspace{0.2cm} d_{0}=0.2 \hspace{0.05cm},\hspace{0.2cm} d_{1}=0.7 \hspace{0.05cm},\hspace{0.2cm} d_{2}=0.5 \hspace{0.05cm},\hspace{0.2cm} d_{3}=0 \hspace{0.05cm} \hspace{0.05cm}.\]

Das Baumdiagramm mit den Knoten γ_ν(i) ist unten dargestellt. Für die Zeitpunkte ν = 0 bis ν = 3 gilt:

\[\nu = 0 : \hspace{0.2cm}\varepsilon_{0}(00) = [0.2- (0 \cdot 0.7 + 0 \cdot 0.3)]^2=0.04 \hspace{0.05cm},\]

\[\hspace{0.4cm} \varepsilon_{0}(01) = [0.2- (0 \cdot 0.7 + 1 \cdot 0.3)]^2=0.01 \hspace{0.05cm},\]

\[\nu = 1 : \hspace{0.2cm}\varepsilon_{1}(00) = [0.7- (0 \cdot 0.7 + 0 \cdot 0.3)]^2=0.49 \hspace{0.05cm},\]

\[\hspace{0.4cm} \varepsilon_{1}(01) = [0.7- (0 \cdot 0.7 + 1 \cdot 0.3)]^2=0.16 \hspace{0.05cm},\]

\[\hspace{0.4cm}\varepsilon_{1}(10) = [0.7- (1 \cdot 0.7 + 0 \cdot 0.3)]^2=0.00 \hspace{0.05cm}\]

\[\hspace{0.4cm}\varepsilon_{1}(11) = [0.7- (1 \cdot 0.7 + 1 \cdot 0.3)]^2=0.09 \hspace{0.05cm},\]

\[\nu = 2 : \hspace{0.2cm}\varepsilon_{2}(00) = [0.5- (0 \cdot 0.7 + 0 \cdot 0.3)]^2=0.25 \hspace{0.05cm},\]

\[\hspace{0.4cm}\varepsilon_{2}(01) = [0.5- (0 \cdot 0.7 + 1 \cdot 0.3)]^2=0.04 \hspace{0.05cm},\]

\[\hspace{0.4cm}\varepsilon_{2}(10) = [0.5- (1 \cdot 0.7 + 0 \cdot 0.3)]^2=0.04 \hspace{0.05cm},\]

\[\hspace{0.4cm}\varepsilon_{2}(11) = [0.5- (1 \cdot 0.7 + 1 \cdot 0.3)]^2=0.25 \hspace{0.05cm},\]

\[ \nu = 3 : \hspace{0.2cm}\varepsilon_{3}(00) = [0.0- (0 \cdot 0.7 + 0 \cdot 0.3)]^2=0.00 \hspace{0.05cm},\]

\[\hspace{0.4cm}\varepsilon_{3}(01) = [0.0- (0 \cdot 0.7 + 1 \cdot 0.3)]^2=0.09 \hspace{0.05cm},\]

\[\hspace{0.4cm}\varepsilon_{3}(10) = [0.0- (1 \cdot 0.7 + 0 \cdot 0.3)]^2=0.49 \hspace{0.05cm},\]

\[\hspace{0.4cm}\varepsilon_{3}(11) = [0.0- (1 \cdot 0.7 + 1 \cdot 0.3)]^2=1.00 \hspace{0.05cm}.\]

Minimale Gesamtfehlergröße und Trellisdiagramm (1)

Wir gehen weiterhin von den Zahlenwerten des letzten Beispiels aus.

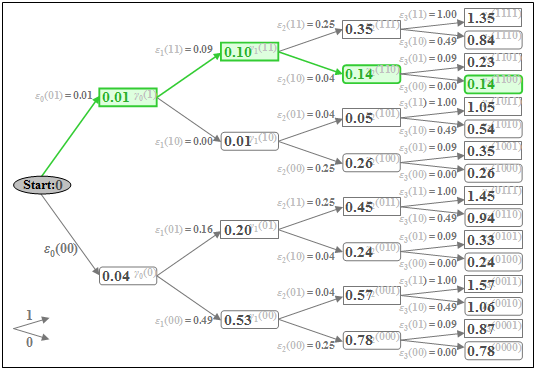
Wichtige Eigenschaften des optimalen Entscheiders (Maximum–Likelihood) lassen sich aus obiger Grafik anhand des Zeitpunktes ν = 2 erkennen:

• Die minimale Gesamtfehlergröße ist γ₂(101) = 0.05 (braun hervorgehoben). Das bedeutet: Eine Entscheidung zu diesem Zeitpunkt – basierend auf den Werten d₀, d₁ und d₂ – wäre zugunsten der Folge „101” anstelle der gesendeten Folge „110” ausgegangen.
  

• Daraus folgt: Für eine optimale Entscheidung sollte eine zu frühe endgültige Festlegung unbedingt vermieden werden. Allerdings kann man zu jedem Zeitpunkt ν bereits mehrere Teilsymbolfolgen ausschließen, die zu späteren Zeitpunkten nicht mehr berücksichtigt werden müssen.
  

• Zu γ₂(001), γ₂(011) und γ₂(111) werden jeweils genau die gleichen Fehlergrößen hinzuaddiert. Da diese drei Metriken alle größer sind als γ₂(101) = 0.05, steht bereits bei ν = 2 fest, dass „001”, „011” sowie „111” nicht Bestandteil der wahrscheinlichsten Folge sein können. Diese Knoten und alle ihre Nachfahren müssen deshalb nicht weiter beachtet werden (braune Überdeckungen).
  

• Gleiches gilt für die abgerundeten Knoten: γ₂(000), γ₂(010) und γ₂(100) sind größer als der grün markierte Knoten γ₂(110) = 0.14, so dass auch diese und ihre Nachfahren ab dem Zeitpunkt ν = 3 nicht mehr berücksichtigt werden müssen (grüne Überdeckungen).
  

• Man stellt fest: Von den acht Knoten bei ν = 2 müssen nur zwei weiterverfolgt werden, nämlich das abgerundete Rechteck γ₂(110) = 0.14 und das Rechteck γ₂(101) = 0.05. Diese beschreiben die minimalen Gesamtfehlergrößen unter der Annahme, dass a₃ = 0 bzw. a₃ = 1 sein wird.
  
  

Die Beschreibung wird auf der nächsten Seite fortgesetzt.