Structure of the Optimal Receiver

Blockschaltbild und Voraussetzungen

In diesem Kapitel wird die Struktur des optimalen Empfängers eines digitalen Übertragungssystems sehr allgemein hergeleitet, wobei

das Modulationsverfahren und weitere Systemdetails nicht weiter spezifiziert werden,
von den Basisfunktionen und der Signalraumdarstellung gemäß Kapitel 4.1 ausgegangen wird..

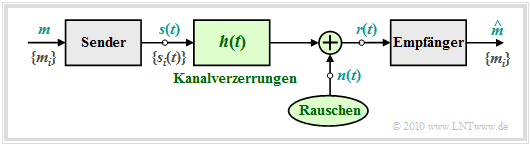
Zum obigen Blockschaltbild ist anzumerken:

Der Symbolumfang der Quelle beträgt M und der Symbolvorrat ist {m_i} mit i = 0, ... , M – 1. Die zugehörigen Symbolwahrscheinlichkeiten Pr(m = m_i) seien auch dem Empfänger bekannt.

Zur Nachrichtenübertragung stehen M verschiedene Signalformen s_i(t) zur Verfügung, wobei für die Laufvariable ebenfalls die Indizierung i = 0, ... , M – 1 gelten soll.

Es besteht eine feste Beziehung zwischen den Nachrichten {m_i} und den Signalen {s_i(t)}. Wird die Nachricht m = m_i übertragen, so ist das Sendesignal s(t) = s_i(t).

Lineare Kanalverzerrungen sind in der obigen Grafik durch die Impulsantwort h(t) berücksichtigt. Außerdem ist ein (irgendwie geartetes) Rauschen n(t) wirksam.

Mit diesen beiden die Übertragung störenden Effekten lässt sich das am Empfänger ankommende Signal r(t) in folgender Weise angeben:

$r(t) = s(t) \star h(t) + n(t) \hspace{0.05cm}.$

Aufgabe des (optimalen) Empfängers ist es, anhand seines Eingangssignals r(t) herauszufinden, welche der M möglichen Nachrichten m_i – bzw. welches der Signale s_i(t) – gesendet wurde.

Der vom Empfänger gefundene Schätzwert für m wird in Gleichungen durch ein „Circonflexe” (^) gekennzeichnet. Im Fließtext (HTML–Zeichensatz) ist diese Darstellung leider nicht möglich.

Man spricht von einem optimalen Empfänger, wenn die Symbolfehlerwahrscheinlichkeit den für die Randbedingungen kleinstmöglichsten Wert annimmt:

$p_{\rm S} = {\rm Pr} ({\cal E}) = {\rm Pr} ( \hat{m} \ne m) \hspace{0.15cm} \Rightarrow \hspace{0.15cm}{\rm Minimum} \hspace{0.05cm}.$

Hinweis: Im Folgenden wird meist r(t) = s(t) + n(t) vorausgesetzt, was bedeutet, dass h(t) = δ(t) als verzerrungsfrei angenommen wird. Andernfalls könnten wir die Signale s_i(t) als s'_i(t) = s_i(t) ∗ h(t) neu definieren, also die deterministischen Kanalverzerrungen dem Sendesignal beaufschlagen.

Fundamentaler Ansatz zum optimalen Empfängerentwurf (1)

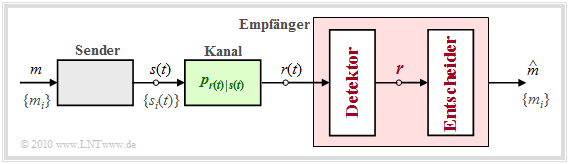
Gegenüber dem auf der vorherigen Seite gezeigten Blockschaltbild führen wir nun einige wesentliche Verallgemeinerungen durch:

Der Übertragungskanal wird durch die bedingte Wahrscheinlichkeitsdichtefunktion p_r(t)|s(t) beschrieben, welche die Anhängigkeit des Empfangssignals r(t) vom Sendesignal s(t) festlegt.

Wurde nun ein ganz bestimmtes Signal r(t) = ρ(t) empfangen, so hat der Empfänger die Aufgabe, anhand dieses Signals ρ(t) sowie der M bedingten Wahrscheinlichkeitsdichtefunktionen

$p_{r(t) | s(t) } (\rho(t) | s_i(t))\hspace{0.2cm}{\rm mit}\hspace{0.2cm} i = 0, ... \hspace{0.05cm}, M-1$

unter Berücksichtigung aller möglichen Sendesignale s_i(t) und deren Auftrittswahrscheinlichkeiten Pr(m = m_i) herauszufinden, welche der möglichen Nachrichten (m_i) bzw. welches der möglichen Signale (s_i(t)) am wahrscheinlichsten gesendet wurde.

Die Schätzung des optimalen Empfängers ist also ganz allgemein bestimmt durch die Gleichung

$\hat{m} = {\rm arg} \max_i \hspace{0.1cm} p_{s(t) | r(t) } ( s_i(t) | \rho(t)) = {\rm arg} \max_i \hspace{0.1cm} p_{m | r(t) } ( m_i | \rho(t))\hspace{0.05cm},$

wobei wieder berücksichtigt ist, dass die gesendete Nachricht m = m_i und das gesendete Signal s(t) = s_i(t) eineindeutig ineinander übergeführt werden können.

In anderen Worten: Der optimale Empfänger betrachtet diejenige Nachricht m_i als die gesendete, wenn die bedingte Wahrscheinlichkeitsdichtefunktion p_m|r(t) für das anliegende Empfangssignal ρ(t) sowie unter der Annahme m = m_i den größtmöglichen Wert annimmt.

Bevor wir die obige Entscheidungsregel näher diskutieren, soll der optimale Empfänger entsprechend der Grafik noch in zwei Funktionsblöcke aufgeteilt werden:

Der Detektor nimmt am Empfangssignal r(t) verschiedene Messungen vor und fasst diese im Vektor r zusammen. Bei K Messungen entspricht r einem Punkt im K–dimensionalen Vektorraum.

Der Entscheider bildet abhängig von diesem Vektor den Schätzwert. Bei einem gegebenen Vektor r = ρ lautet dabei die Entscheidungsregel:

$\hat{m} = {\rm arg} \max_i \hspace{0.1cm} P_{m | \boldsymbol{ r} } ( m_i | \boldsymbol{\rho}) \hspace{0.05cm}.$

Im Gegensatz zur oberen Gleichung tritt nun in der Entscheidungsregel eine bedingte Wahrscheinlichkeit P_m|r anstelle der bedingten Wahrscheinlichkeitskeitsdichtefunktion (WDF) p_m|r(t) auf. Beachten Sie bitte die Groß– bzw. Kleinschreibung für die unterschiedlichen Bedeutungen.