Exercise 2.2Z: Power Consideration
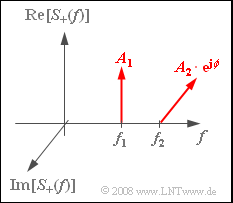
Wir betrachten zwei harmonische Schwingungen $$ s_1(t) = A_1 \cdot \cos(\omega_{\rm 1} \cdot t ) \hspace{0.05cm},$$ $$s_2(t) = A_2 \cdot \cos(\omega_{\rm 2} \cdot t + \phi) \hspace{0.05cm},$$ wobei für die Frequenzen $f_2 ≥ f_1$ gelten soll. Die Grafik zeigt das Spektrum des analytischen Signals $s_+(t)$, das sich additiv aus den beiden Anteilen $s_{1+}(t)$ und $s_ {2+}(t)$ zusammensetzt.
Unter der Sendeleistung $P_S$ soll hier der quadratische Mittelwert des Signals $s(t)$ verstanden werden, gemittelt über eine möglichst große Messdauer:
$$P_{\rm S} = \lim_{T_{\rm M} \rightarrow \infty}\hspace{0.1cm}\frac{1}{T_{\rm M}} \cdot \int_{0}^{ T_{\rm M}} {s^2(t) }\hspace{0.1cm}{\rm d}t \hspace{0.05cm}.$$
Beschreibt $s(t)$ einen Spannungsverlauf, so besitzt $P_S$ nach dieser Definition die Einheit „V2” und bezieht sich auf den Widerstand $R = 1 Ω$. Die Division durch R liefert die physikalische Leistung in „W”.
Verwenden Sie die Zahlenwerte $A_1 = 2 V$, $A_2 = 1 V$ und $R = 50 Ω$.
Hinweis: Diese Aufgabe bezieht sich auf das Kapitel 1.2 und das Kapitel 2.1.
Fragebogen
Musterlösung