Parameters of Digital Channel Models

Anwendung analoger Kanalmodelle

Für Untersuchungen von Nachrichtenübertragungssystemen sind geeignete Kanalmodelle von großer Wichtigkeit, weil diese

Voraussetzung für eine Systemsimulation und –optimierung sind, sowie
gleichbleibende und rekonstruierbare Randbedingungen schaffen.

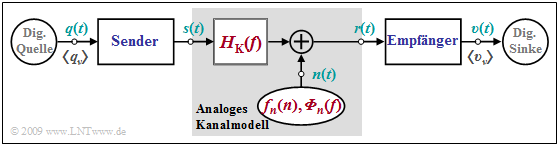
Für die Digitalsignalübertragung gibt es sowohl analoge als auch digitale Kanalmodelle: Ein analoges Kanalmodell muss zwar den Übertragungskanal nicht in allen physikalischen Einzelheiten wiedergeben, sollte jedoch dessen Übertragungsverhalten inklusive der dominanten Störgrößen funktionell ausreichend genau beschreiben. Meist muss ein Kompromiss zwischen mathematischer Handhabbarkeit und dem Bezug zur Realität gefunden werden.

: Die Grafik zeigt ein analoges Kanalmodell innerhalb eines digitalen Übertragungssystems. Dieses beinhaltet den Kanalfrequenzgang H_K(f) zur Beschreibung der linearen Verzerrungen sowie ein additives Störsignal n(t), charakterisiert durch die Wahrscheinlichkeitsdichtefunktion f_n(n) und das Leistungsdichtespektrum Φ_n(f).

Ein Sonderfall dieses Modells ist der so genannte AWGN–Kanal (Additive White Gaussian Noise) mit den Systemeigenschaften

\[H_{\rm K}(f) = 1\hspace{0.05cm},\hspace{0.2cm}{\it \Phi}_{n}(f) = {\rm const.}\hspace{0.05cm},\hspace{0.2cm} {f}_{n}(n) = \frac{1}{\sqrt{2 \pi} \cdot \sigma} \cdot {\rm e}^{-n^2\hspace{-0.05cm}/(2 \sigma^2)}\hspace{0.05cm}.\]

Dieses einfache Modell eignet sich zum Beispiel zur Beschreibung eines Funkkanals mit zeitinvariantem Verhalten, wobei das Kanalmodell dahingehend abstrahiert ist, dass

der eigentlich bandpassartige Kanal im äquivalenten Tiefpassbereich beschrieben wird, und

die vom Frequenzband und der Übertragungsweglänge abhängige Dämpfung mit der Varianz σ² des Rauschsignals n(t) verrechnet wird.

Zur Berücksichtigung zeitvarianter Eigenschaften muss man andere Modelle wie Rayleigh–, Rice– und Lognormal–Fading verwenden, die im Buch „Mobile Kommunikation” beschrieben werden.

Bei leitungsgebundenen Übertragungssystemen ist insbesondere der spezifische Frequenzgang des Übertragungsmediums entsprechend den Angaben in Kapitel 4.2 (Koaxialkabel) und Kapitel 4.3 (Zweidrahtleitung) des Buches „Lineare zeitinvariante Systeme” zu berücksichtigen, aber auch, dass aufgrund von Fremdstörungen (Nebensprechen, elektromagnetische Felder, usw.) nicht mehr von Weißem Rauschen ausgegangen werden kann.

Bei optischen Systemen muss zudem das multiplikativ wirkende, also signalabhängige Schrotrauschen geeignet in das analoge Kanalmodell eingearbeitet werden.