Exercise 4.4: About the Quantization Noise

• Return to book

Zur Berechnung der Quantisierungsrauschleistung $P_Q$ gehen wir von einem periodischen sägezahnförmigen Quellensignal $q(t)$ mit dem Wertebereich $±q_{max}$ und der Periodendauer $T_0$ aus.

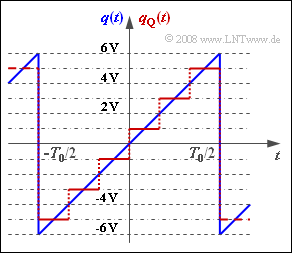
Im mittleren Zeitbereich $–T_0/2 ≤ t ≤ T_0/2$ gilt: $$q(t) = q_{\rm max} \cdot \left ( {2 \cdot t}/{T_0} \right ).$$ Dessen Leistung wird hier mit $P_S$ bezeichnet.

Dieses Signal wird entsprechend der Grafik mit $M = 6$ Stufen quantisiert. Der lineare Quantisierer ist für den Amplitudenbereich $±Q_{max}$ ausgelegt, so dass jedes Quantisierungsintervall die Breite $Δ = 2/M · Q_{max}$ aufweist. Die Grafik zeigt diesen Sachverhalt für $Q_{max} = q_{max} = 6 V$. Von diesen Zahlenwerten soll bis einschließlich Teilaufgabe e) ausgegangen werden.

Die so genannte Quantisierungsrauschleistung ist als der quadratische Mittelwert des Differenzsignals $ε(t) = q_Q(t) – q(t)$ definiert. Es gilt $$P_{\rm Q} = \frac{1}{T_0' } \cdot \int_{0}^{T_0'}\varepsilon(t)^2 \hspace{0.05cm}{\rm d}t \hspace{0.05cm},$$ wobei die Zeit $T_0'$ geeignet zu wählen ist. Als Quantisierungs–SNR bezeichnet man das Verhältnis $$\rho_{\rm Q} = \frac{P_{\rm S}}{P_{\rm Q}}\hspace{0.05cm},$$ das meist in dB angegeben wird.

Hinweis: Die Aufgabe bezieht sich auf das Kapitel 4.1.

Fragebogen

1

Berechnen Sie die Signalleistung $P_S$ (auf 1 Ω bezogen):

$P_S$ = $V^2$

2

Welche Aussagen treffen für das Fehlersignal $ε(t)$ zu?

+ $ε(t)$ hat einen sägezahnförmigen Verlauf.

- $ε(t)$ hat einen stufenförmigen Verlauf.

+ $ε(t)$ ist auf den Bereich $±Δ/2 = ±1V$ beschränkt.

+ $ε(t)$ besitzt die Periodendauer $T_0' = T_0/M$.

3

Wie groß ist die Quantisierungsrauschleistung?

$M=6 P_Q$ = $V^2$

4

Berechnen Sie den Quantisierungsrauschabstand für $M = 6$.

$M = 6: 10 · lg ρ_Q$ = $dB$

5

Welche Werte ergeben sich bei Quantisierung mit $N = 8$ bzw. $N = 16 Bit$?

$ N = 8: 10 · lg ρ_Q$ = $dB$

$ N = 16: 10 · lg ρ_Q$ = $dB$

6

Welche Voraussetzungen müssen erfüllt sein, damit die abgeleitete Gleichung für $ρ_Q$ angewandt werden kann?

	Alle Amplitudenwerte sind gleichwahrscheinlich.
	Es liegt ein linearer Quantisierer vor.
	Der Quantisierer ist genau an das Signal angepasst ($Q_{max} = q_{max}$).

Musterlösung

Solution

1. Die Signalleistung $P_S$ ist gleich dem quadratischen Mittelwert von $q(t)$, wenn der Bezugswiderstand 1Ω verwendet und dementsprechend für die Leistung die Einheit „$V^2$” in Kauf genommen wird. Aufgrund der Periodizität und der Symmetrie genügt die Mittelung über $T_0/2$: $$P_{\rm S} = \frac{1}{T_0/2} \cdot \int\limits_{0}^{T_0/2}q^2(t) \hspace{0.05cm}{\rm d}t = \frac{2 \cdot q_{\rm max}^2}{T_0} \cdot \int\limits_{0}^{T_0/2}\left ( { 2 \cdot t}/{T_0} \right )^2 \hspace{0.05cm}{\rm d}t=$$ $$ = \frac{2 \cdot q_{\rm max}^2}{T_0} \cdot \frac{T_0}{2} \cdot \int\limits_{0}^{1}x^2 \hspace{0.05cm}{\rm d}x = \frac{q_{\rm max}^2}{3} \hspace{0.05cm}.$$ Hierbei wurde die Substitution $x = 2 · t/T_0$ verwendet. Mit $q_{max} = 6 V$ erhält man $P_S = 12 V^2$.

2. Wir gehen hier von $Q_{max} = q_{max} = 6 V$ aus. Damit ergibt sich das sägezahnförmige Fehlersignal $ε(t)$ zwischen $±1V$ und der Periodendauer $T0' = T_0/6$.

Richtig sind also die Lösungsvorschläge 1, 3 und.4. 3. 4. 5. 6. 7.