Exercise 3.1Z: Hilbert Transform

• Return to book

Considered impulse responses

The relation between the real part and the imaginary part of the transfer function of realizable causal systems is described by the Hilbert transformation.  Here, the following holds:

$${\rm Im} \left\{ H(f) \right \} = - \frac{1}{\pi }\int_{-\infty}^{ +\infty} { \frac{{\rm Re} \left\{ H(\nu) \right \}}{f - \nu}}\hspace{0.1cm}{\rm d}\nu \hspace{0.05cm},$$

$${\rm Re} \left\{ H(f) \right \} = \frac{1}{\pi }\int_{-\infty}^{ +\infty} { \frac{{\rm Im} \left\{ H(\nu) \right \}}{f - \nu}}\hspace{0.1cm}{\rm d}\nu \hspace{0.05cm}.$$

The following is used as a common abbreviation for these two integral transformations:

$${\rm Im} \left\{ H(f) \right \} \quad \bullet\!\!-\!\!\!-\!\!\!-\!\!\hspace{-0.05cm}\rightarrow\quad {\rm Re} \left\{ H(f) \right \}\hspace{0.05cm}.$$

Since the transformation and its inverse differ only by the sign,  one equation is sufficient.  Here, the following applies:

• To compute the operand marked by the arrow the positive sign is used.

• In contrast to this,  the minus sign is taken into account for the computation of the operand marked by the circle.

The Hilbert transformation pertains much more generally than only to the case of application described here.  For example,  it is also used to determine the (complex) analytical signal corresponding to a real band-pass signal.

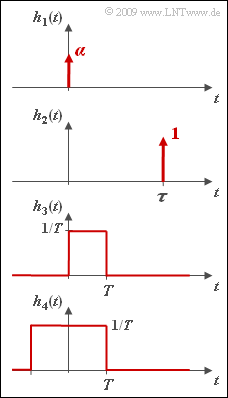
In this exercise,  the corresponding frequency responses  $H(f)$  are to be determined for the causal impulse responses  $h(t)$  given in the diagram according to the inverse Fourier transformation.

If  $H(f)$  is decomposed into real and imaginary parts respectively,  then Hilbert correspondences can be derived from it.

Please note:

• The exercise belongs to the chapter  Conclusions from the Allocation Theorem.
• In particular, reference is made to the theory page  Hilbert transform.

Questions

1

Determine the Hilbert transform of a constant  $\alpha$ beginning with  $h_1(t) = \alpha \cdot \delta(t)$ .
Which statements are true?

	The Hilbert transform of a constant  $\alpha$  is also  $\alpha$.
	The Hilbert transform of a constant  $\alpha$  is zero.
	The Hilbert transform of a constant  $\alpha$  is sinusoidal.

2

Determine the Hilbert transform of a cosine function beginning with  $h_2(t) = \delta(t- \tau)$ .
Which statements are true?

	The Hilbert transform of a cosine is a constant.
	The Hilbert transform of a cosine function is zero.
	The Hilbert transform of a cosine is sinusoidal.

3

Determine the Hilbert transform of the function  ${\rm si}(2 \pi fT) = {\rm sin}(2 \pi fT)/(2 \pi fT)$ beginning with the rectangular  $h_3(t)$ .
Which statements are true?

	The Hilbert transform is  ${\rm sin}^2\hspace{-0.05cm}(\pi fT)/(\pi fT)$.
	The Hilbert transform is  ${\rm sin}( \pi fT) \cdot {\rm si}( \pi fT)$.

4

Can a Hilbert correspondence be derived from the impulse response  $h_4(t)$ ?

	Yes.
	No.

Solution

Solution

(1)  The  second proposed solution  is correct:

• The Fourier transform of  $h_1(t) = \alpha \cdot \delta(t)$  is:

$$H_1(f) = \alpha \hspace{0.3cm}\Rightarrow \hspace{0.3cm}{\rm Re} \left\{ H_1(f) \right \} = \alpha , \hspace{0.2cm}{\rm Im} \left\{ H_1(f) \right \} = 0\hspace{0.05cm}.$$

(2)  The  last proposed solution  is correct:

• The following frequency response is obtained for the impulse response  $h_2(t)$  considering the  shifting theorem  and  Euler's theorem :

$$H_2(f) ={\rm e}^{-{\rm j}\hspace{0.05cm} 2\pi f \tau} = \cos (2\pi f \tau) - {\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm} \sin (2\pi f \tau)\hspace{0.05cm}.$$

• This results in the Hilbert correspondence

$$\cos (2\pi f \tau) \hspace{0.3cm} \leftarrow\hspace{-0.05cm}\!\!-\!\!\!-\!\!\!-\!\!\bullet\hspace{0.3cm} -\sin (2\pi f \tau)\hspace{0.7cm}{\rm or}\hspace{0.7cm} \cos (2\pi f \tau) \hspace{0.3cm} \bullet\hspace{-0.05cm}\!\!-\!\!\!-\!\!\!-\!-\!\hspace{-0.1cm}\rightarrow\hspace{0.3cm} \sin (2\pi f \tau) \hspace{0.05cm}.$$

(3)  Both proposed solutions  are correct:

• For the rectangular impulse response  $h_3(t)$  of width  $T$  and height  $1/T$  the spectral function is obtained according to the  first Fourier integral:

$$H_3(f) = \int_{-\infty}^{ +\infty} { h_3(t) \hspace{0.05cm}\cdot \hspace{0.05cm} {\rm e}^{-{\rm j}\hspace{0.05cm} 2\pi f t}}\hspace{0.1cm}{\rm d}t \hspace{0.05cm} = \frac{1}{T} \cdot \int_{0}^{ T} { {\rm e}^{-{\rm j}\hspace{0.05cm} 2\pi f t}}\hspace{0.1cm}{\rm d}t = \left [\frac{1}{-{\rm j}\cdot 2\pi f T} \cdot {\rm e}^{-{\rm j}\hspace{0.05cm} 2\pi f\hspace{0.05cm} t} \right ]_{0}^{T} = \frac{1-{\rm e}^{-{\rm j}\hspace{0.05cm} 2\pi f\hspace{0.05cm} T}}{{\rm j}\cdot 2\pi f T} \hspace{0.05cm}.$$

• Using  Euler's theorem  this can also be rewritten as follows:

$$H_3(f) = \frac{1-\cos (2\pi f T) + {\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm} \sin (2\pi f T)}{{\rm j}\cdot 2\pi f T} = \frac{\sin (2\pi f T)}{ 2\pi f T} - {\rm j}\cdot \frac{1 - \cos (2\pi f T)}{ 2\pi f T}\hspace{0.05cm}.$$

• Furthermore, the following holds considering the transformation  $1 - \cos(\alpha) = 2 \cdot \sin^2(\alpha/2)$:

$${\rm Re}\hspace{-0.05cm} \left\{ H_3(f) \right \} = {\rm si} (2\pi f T)\hspace{0.2cm}{\rm mit}\hspace{0.2cm}{\rm si}(x)= {\rm sin}(x)/x \hspace{0.05cm}, \hspace{0.5cm} {\rm Im} \hspace{-0.05cm}\left\{ H_3(f) \right \} = -\frac{\sin^2 (\pi f T)}{ \pi f T}= - {\rm si} (\pi f T) \cdot {\rm sin} (\pi f T) \hspace{0.05cm}.$$

(4)  No is correct:

• The impulse response   $h_4(t)$  is not causal so that no Hilbert correspondence can be derived from the associated Fourier spectrum  $H_4(f)$ .