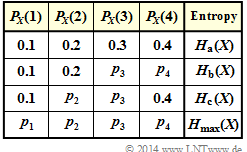
Exercise 3.4: Entropy for Different PMF

• Return to book

Probability functions, each with  $M = 4$  elements

In the first row of the adjacent table, the probability mass function denoted by  $\rm (a)$  is given in the following.

For this PMF  $P_X(X) = \big [0.1, \ 0.2, \ 0.3, \ 0.4 \big ]$  the entropy is to be calculated in subtask  (1) :

$$H_{\rm a}(X) = {\rm E} \big [ {\rm log}_2 \hspace{0.1cm} \frac{1}{P_{X}(X)}\big ]= - {\rm E} \big [ {\rm log}_2 \hspace{0.1cm}{P_{X}(X)}\big ].$$

Since the logarithm to the base  $2$  is used here, the pseudo-unit  "bit"  is to be added.

In the further tasks, some probabilities are to be varied in each case in such a way that the greatest possible entropy results:

• By suitably varying  $p_3$  and  $p_4$,  one arrives at the maximum entropy  $H_{\rm b}(X)$  under the condition  $p_1 = 0.1$  and  $p_2 = 0.2$   ⇒   subtask  (2).
• By varying  $p_2$  and  $p_3$ appropriately, one arrives at the maximum entropy  $H_{\rm c}(X)$  under the condition  $p_1 = 0.1$  and  $p_4 = 0.4$   ⇒   subtask  (3).
• In subtask  (4)  all four parameters are released for variation,  which are to be determined according to the maximum entropy   ⇒   $H_{\rm max}(X)$ .

Hints:

• The exercise belongs to the chapter  Some preliminary remarks on two-dimensional random variables.
• In particular, reference is made to the page  Probability mass function and entropy.

Questions

1

To which entropy does the probability mass function  $P_X(X) = \big [ 0.1, \ 0.2, \ 0.3, \ 0.4 \big ]$ lead?

$H_{\rm a}(X) \ = \ $ $\ \rm bit$

2

Let  $P_X(X) = \big [ 0.1, \ 0.2, \ p_3, \ p_4\big ]$ apply in general.  What entropy is obtained if  $p_3$  and  $p_4$  are chosen as best as possible?

$H_{\rm b}(X) \ = \ $ $\ \rm bit$

3

Now let  $P_X(X) = \big [ 0.1, \ p_2, \ p_3, \ 0.4 \big ]$.  What entropy is obtained if  $p_2$  and  $p_3$  are chosen as best as possible?

$H_{\rm c}(X) \ = \ $ $\ \rm bit$

4

What entropy is obtained if all probabilities  $(p_1, \ p_2 , \ p_3, \ p_4)$  can be chosen as best as possible?

$H_{\rm max}(X) \ = \ $ $\ \rm bit$

Solution

Solution

(1)  With  $P_X(X) = \big [ 0.1, \ 0.2, \ 0.3, \ 0.4 \big ]$  we get for the entropy:

$$H_{\rm a}(X) = 0.1 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.1} + 0.2 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.2} + 0.3 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.3} + 0.4 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.4} \hspace{0.15cm} \underline {= 1.846} \hspace{0.05cm}.$$

Here (and in the other tasks) the pseudo-unit  "bit"  is to be added in each case.

(2)  The entropy  $H_{\rm b}(X)$  can be represented as the sum of two parts  $H_{\rm b1}(X)$  and  $H_{\rm b2}(X)$,  with:

$$H_{\rm b1}(X) = 0.1 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.1} + 0.2 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.2} = 0.797 \hspace{0.05cm},$$

$$H_{\rm b2}(X) = p_3 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{p_3} + (0.7-p_3) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.7-p_3} \hspace{0.05cm}.$$

• The second function is maximum for  $p_3 = p_4 = 0.35$.  A similar relationship has been found for the binary entropy function.  
• Thus one obtains:

$$H_{\rm b2}(X) = 2 \cdot p_3 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{p_3} = 0.7 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.35} = 1.060$$

$$\Rightarrow \hspace{0.3cm} H_{\rm b}(X) = H_{\rm b1}(X) + H_{\rm b2}(X) = 0.797 + 1.060 \hspace{0.15cm} \underline {= 1.857} \hspace{0.05cm}.$$

(3)  Analogous to subtask  (2),  $p_1 = 0.1$  and  $p_4 = 0.4$  yield the maximum for  $p_2 = p_3 = 0.25$:

$$H_{\rm c}(X) = 0.1 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.1} + 2 \cdot 0.25 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.25} + 0.4 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.4} \hspace{0.15cm} \underline {= 1.861} \hspace{0.05cm}.$$

(4)  The maximum entropy for the symbol range  $M=4$  is obtained for equal probabilities, i.e. for  $p_1 = p_2 = p_3 = p_4 = 0.25$:

$$H_{\rm max}(X) = {\rm log}_2 \hspace{0.1cm} M \hspace{0.15cm} \underline {= 2} \hspace{0.05cm}.$$

• The difference of the entropies according to  (4)  and  (3)  gives  ${\rm \Delta} H(X) = 0.139 \ \rm bit$.  Here:

$${\rm \Delta} H(X) = 1- 0.1 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.1} - 0.4 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.4} \hspace{0.05cm}.$$

• With the binary entropy function

$$H_{\rm bin}(p) = p \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{p} + (1-p) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{1-p}$$

can also be written for this:

$${\rm \Delta} H(X) = 0.5 \cdot \big [ 1- H_{\rm bin}(0.2) \big ] = 0.5 \cdot \big [ 1- 0.722 \big ] = 0.139 \hspace{0.05cm}.$$