Exercise 4.6: OVSF Codes

Tree structure for the construction
of an OVSF code

The spreading codes for UMTS should

all be orthogonal to each other to avoid mutual interference between subscribers,
be as flexible as possible in order to realize different spreading factors $J$ .

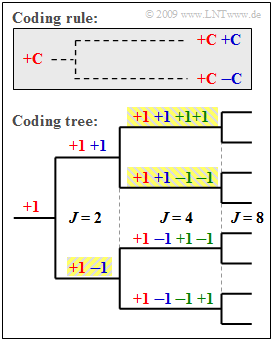
An example of this are the so-called Orthogonal Variable Spreading Factor (OVSF) codes, which provide spreading codes of lengths from $J = 4$ to $J = 512$ . These can be created using a code tree, as shown in the diagram. Thereby, at each branch from one code $\mathcal{C}$ two new codes are created.

$(+\mathcal{C} \ +\hspace{-0.05cm}\mathcal{C})$,
$(+\mathcal{C}\ -\hspace{-0.05cm}\mathcal{C})$.

The diagram illustrates the principle given here by the example $J = 4$.

If we number the spreading sequences from $0$ to $J -1$ we get here the spreading sequences

$$ \langle c_\nu^{(0)}\rangle \ = \ {+\hspace{-0.05cm}1}\hspace{0.15cm} {+\hspace{-0.05cm}1} \hspace{0.15cm} {+\hspace{-0.05cm}1}\hspace{0.15cm} {+\hspace{-0.05cm}1} \hspace{0.05cm},\hspace{0.3cm} \langle c_\nu^{(1)}\rangle = {+\hspace{-0.05cm}1}\hspace{0.15cm} {+\hspace{-0.05cm}1} \hspace{0.15cm} {-\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.05cm},$$

$$\langle c_\nu^{(2)}\rangle \ = \ {+\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.15cm} {+\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.05cm},\hspace{0.3cm} \langle c_\nu^{(3)}\rangle = {+\hspace{-0.05cm}1}\hspace{0.15cm} {-\hspace{-0.05cm}1} \hspace{0.15cm} {-\hspace{-0.05cm}1}\hspace{0.15cm} {+\hspace{-0.05cm}1} \hspace{0.05cm}.$$

According to this nomenclature, for the spreading factor $J = 8$ there are the spreading sequences $\langle c_{\nu}^{(0)} \rangle, \ \text{...} \ ,\langle c_{\nu}^{(7)} \rangle$.

Note that no predecessor and successor of a code may be used by other participants.

So, in the example, four spreading codes with spreading factor $J = 4$ could be used, or.
the three codes highlighted in yellow - once with $J = 2$ and twice with $J = 4$.

Hints:

This exercise belongs to the chapter "Telecommunications Aspects of UMTS".
Reference is made in particular to the page "Spreading codes and scrambling with UMTS".

Questions

	$\langle c_{\nu}^{(1)} \rangle = +1 +1 +1 -1 -1 -1$,
	$\langle c_{\nu}^{(3)} \rangle = +1 +1 -1 +1 -1 -1$,
	$\langle c_{\nu}^{(5)} \rangle = +1 -1 +1 -1 +1 +1$,
	$\langle c_{\nu}^{(7)} \rangle = +1 -1 -1 +1 +1 -1$.

$K_{\rm max} \ = \ $

$K \ = \ $

	Yes.
	No.

Solution

OVSF tree structure for $J = 8$

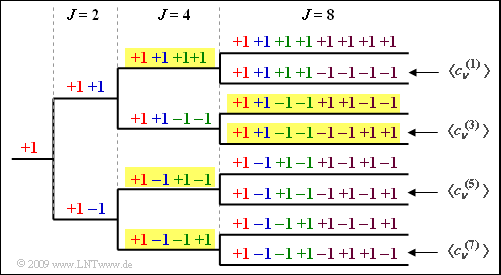
(1) The graph shows the OVSF tree structure for $J = 8$ user.

From this it can be seen that proposed solutions 1, 3, and 4 are true, but not the second one.

(2) If each user is assigned a spreading code with $J = 8$ then $\underline{K_{\rm max} = 8}$ subscribers can be served.

(3) If three subscribers are served with $J = 4$ only two subscribers can be served by a spreading sequence with $J = 8$ (see exemplary yellow background in above diagram) ⇒ $\underline{K = 5}$.

(4) We denote by.

$K_{4} = 2$ the number of spreading sequences with $J = 4$,
$K_{8} = 1$ the number of spreading sequences with $J = 8$,
$K_{16} = 2$ the number of spreading sequences with $J = 16$,
$K_{32} = 8$ the number of spreading sequences with $J = 32$.

Then the following condition must be satisfied:

$$ K_4 \cdot \frac{32}{4} + K_8 \cdot \frac{32}{8} +K_{16} \cdot \frac{32}{16} +K_{32} \cdot \frac{32}{32} \le 32 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} K_4 \cdot8 + K_8 \cdot 4 +K_{16} \cdot2 +K_{32} \cdot1 \le 32 \hspace{0.05cm}.$$

Because $2 \cdot 8 + 1 \cdot 4 + 2 \cdot 2 + 8 = 32$ the desired allocation is just allowed ⇒ Answer YES.
Providing the degree of spread twice $J = 4$ blocks, for example, the top half of the tree, after providing one spread with $J = 8$, three of the eight branches remain to be occupied at the $J = 8$ level, and so on.