Exercise 5.2Z: DFT of a Triangular Pulse

• Return to book

Discretisation of a triangular pulse

Consider the sketched triangular pulse

$$x(t) = \left\{ \begin{array}{l} A \cdot \left( 1 - {|t|}/{T} \right ) \\ \hspace{0.25cm} 0 \\ \end{array} \right.\quad \begin{array}{*{10}c} {\rm{for}} \\ {\rm{for}} \\ \end{array}\begin{array}{*{10}c} {\left| \hspace{0.005cm} t\hspace{0.05cm} \right| \le T,} \\ {\left|\hspace{0.005cm} t \hspace{0.05cm} \right| > T.} \\ \end{array}$$

The signal parameters have the following values:

• amplitude  $A = 4 \ \text{V}$,

• equivalent pulse duration  $\Delta t = T = 1 \, \text{ms}$.

The spectrum  $X(f)$  is obtained by applying  the first Fourier Integral:

$$X(f) = A \cdot T \cdot {\rm si}^2(\pi f T)\hspace{0.5cm}\text{with}\hspace{0.5cm}{\rm si}(x)=\sin(x)/x\hspace{0.05cm}.$$

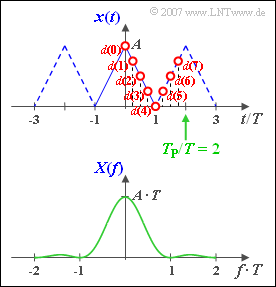
The spectral function is now to be approximated by a  Discrete Fourier Transform  $\rm (DFT)$  with  $N = 8$ , where the   $N$  coefficients for the time domain   ⇒   $d(0)$, ... , $d(7)$  can be taken from the graph.

The corresponding spectral coefficients  $D(0)$, ... ,  $D(7)$  are to be determined.  For the indices  $\mu = 0$, ... , $N–1$  applies:

$$D(\mu) = \frac{1}{N} \cdot \sum_{\nu = 0 }^{N-1} d(\nu)\cdot {w}^{\hspace{0.05cm}\nu \hspace{0.05cm} \cdot \hspace{0.05cm}\mu} \hspace{0.05cm}.$$

If we denote the distance between two samples in the time domain by  $T_{\rm A}$  and the corresponding frequency distance between two lines by $f_{\rm A}$, following relationship applies:

$$N \cdot f_{\rm A} \cdot T_{\rm A} = 1 \hspace{0.05cm}.$$

Hints:

• This task belongs to the chapter  Discrete Fourier Transformation (DFT).

• The topic dealt with here is also dealt with in the interactive applet  Discrete Fourier Transform and Inverse.

Question

1

Give the time coefficients. What are the values of  $d(0)$,  $d(3)$  and  $d(6)$?

$d(0)\ = \ $  $\text{V}$

$d(3)\ = \ $  $\text{V}$

$d(6)\ = \ $  $\text{V}$

2

What is the distance  $T_{\rm A}$  between two time samples?

$T_{\rm A}\ = \ $  $\text{ms}$

3

What is the distance  $f_{\rm A}$  between two DFT frequency samples?

$f_{\rm A}\ = \ $  $\text{kHz}$

4

Calculate the coefficient  $D(0)$  and interpret the result.

$D(0)\ = \ $  $\text{V}$

5

Calculate the coefficient  $D(2)$  and interpret the result, also in terms of the coefficients  $D(4)$  and  $D(6)$.

$D(2)\ = \ $  $\text{V}$

6

Calculate and interpret the DFT coefficient  $D(7)$.

$D(7)\ = \ $  $\text{V}$

Solution

Solution

(1)  From the graph the following values result with  $A = 4 \ {\rm V}$ :

$${d(0) = 4\,{\rm V}, \hspace{0.1cm}d(1) = d(7) = 3\,{\rm V}, \hspace{0.1cm} \hspace{0.1cm}d(2) = d(6) = 2\,{\rm V}, \hspace{0.1cm} \hspace{0.1cm}d(3) = d(5) = 1\,{\rm V}, \hspace{0.1cm} \hspace{0.1cm}d(4) = 0}\hspace{0.05cm}.$$

$$\Rightarrow \hspace{0.15 cm}\underline{d(0) = 4\,{\rm V}, \hspace{0.1cm}d(3) = 1\,{\rm V}, \hspace{0.1cm}d(6) = 2\,{\rm V}. \hspace{0.1cm}} \hspace{0.05cm}$$

(2)  According to the diagram  $T_{\rm A} = T/4$.

• With  $T = 1 \ \text{ms}$  one obtains  $\underline{T_{\rm A} = 0.25 \ \text{ms}}$.

(3)  For the distances of the samples in the time and frequency domain applies:

$$N \cdot f_{\rm A} \cdot T_{\rm A} = 1 \hspace{0.3cm}\Rightarrow \hspace{0.3cm}f_{\rm A}= \frac{1}{ 8 \cdot 0.25\, {\rm ms}}\hspace{0.15 cm}\underline{= 0.5\, {\rm kHz}}\hspace{0.05cm}.$$

(4)  With  $N = 8$  and  $\mu = 0$ , it follows from the DFT equation:

$$D(0) = \frac{1}{8}\cdot \sum_{\nu = 0 }^{7} d(\nu) = \frac{1\,{\rm V}}{8}\cdot (4+3+2+1+0+1+2+3)\hspace{0.15 cm}\underline{= 2 \,{\rm V}}\hspace{0.05cm}.$$

• The DFT value $D(0)$ describes the spectral value at  $f = 0$, where the following relation holds:

$$X(f=0) = \frac{D(0)}{f_{\rm A}}= \frac{ 2\,{\rm V}}{0.5\,{\rm kHz}}= 4 \cdot 10^{-3}\,{\rm V/Hz}\hspace{0.05cm}.$$

• This value agrees with the theoretical value   $(A \cdot T)$ .

(5)  With  $N = 8$  and  $\mu = 2$  we obtain:

$$D(2) = \frac{1}{8}\cdot \sum_{\nu = 0 }^{7} d(\nu)\cdot {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} (\pi /2) \hspace{0.05cm}\cdot \hspace{0.05cm} \nu} = \frac{1}{8}\cdot \sum_{\nu = 0 }^{7} d(\nu)\cdot (-{\rm j})^{\nu} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} = \frac{1\,{\rm V}}{8}\cdot (4-3\cdot{\rm j}-2+{\rm j}-{\rm j}-2+3\cdot{\rm j})\hspace{0.15 cm}\underline{= 0}\hspace{0.05cm}.$$

This result could have been predicted without calculation:

• The DFT coefficients  $D(\mu)$  are at the same time the Fourier coefficients of the function  $x_{\rm Per}(t)$  periodised at the distance  $T_{\rm P} = 2T$.
  This is shown as a dashed line in the graph on the information page.
• Due to symmetry properties, however, all even Fourier coefficients of the function  $x_{\rm Per}(t)$  are equal to zero   ⇒   $D(4)\hspace{0.15cm}\underline{=0},$   $D(6)\hspace{0.15cm}\underline{=0}$.

(6)  The coefficient  $D(7)$  describes the periodised spectral function at the frequency  $f = 7 \cdot f_{\rm A}$.  Due to periodicity and symmetry property holds:

$$D(7) = D(-1) = D^{\star}(1) \hspace{0.05cm}.$$

Preferably, we calculate this DFT coefficient:

$$D(1) = \frac{1}{8}\cdot \sum_{\nu = 0 }^{7} d(\nu)\cdot {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} (\pi /4) \hspace{0.05cm}\cdot \hspace{0.05cm} \nu} = \frac{1\,{\rm V}}{8}\cdot \left(4 +3\cdot \frac{1 - {\rm j}}{\sqrt{2}}-2\cdot {\rm j}+ \frac{-1 - {\rm j}}{\sqrt{2}}-{\rm j}+ \frac{-1 + {\rm j}}{\sqrt{2}}-{\rm j}+ 2\cdot {\rm j}+3\cdot \frac{1 - {\rm j}}{\sqrt{2}}\right)$$

$$\Rightarrow \; \; D(1) = \frac{2 + \sqrt{2}}{4} \approx 0.854{\rm V}\hspace{0.05cm}.$$

Since  $D(1)$  is purely real,  $D(7) = D(1) \; \underline{= 0.854 \ {\rm V}}$.

This gives for the corresponding values of the continuous spectral function:

$$X(f=-f_{\rm A}) = X(f=+f_{\rm A}) =\frac{D(1)}{f_{\rm A}}= 1.708 \cdot 10^{-3}\,{\rm V/Hz}\hspace{0.05cm}.$$

• Because of the implicit periodic continuation by the DFT, the value calculated in this way does not exactly match the actual value  $(4 \cdot A \cdot T/\pi^2 = 1.621 · 10^{-3}\text{ V/Hz})$.
• The relative error is approx.  $5.3\%$.