Exercise 1.10: BPSK Baseband Model

Unbalanced channel frequency response

In this exercise, we consider a BPSK system with coherent demodulation, i.e.

$$s(t) \ = \ z(t) \cdot q(t),$$

$$b(t) \ = \ 2 \cdot z(t) \cdot r(t) .$$

The designations chosen here are based on the "block diagram" in the theory section.

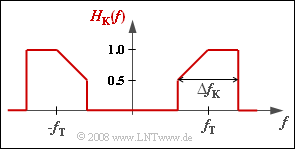
The influence of a channel frequency response $H_{\rm K}(f)$ can be taken into account in a simple way if it is described together with modulator and demodulator by a common baseband frequency response:

$$H_{\rm MKD}(f) = {1}/{2} \cdot \big [ H_{\rm K}(f-f_{\rm T}) + H_{\rm K}(f+f_{\rm T})\big ] .$$

Thus the modulator and demodulator are virtually shortened against each other, and

the band-pass channel $H_{\rm K}(f)$ is transformed into the low-pass range.

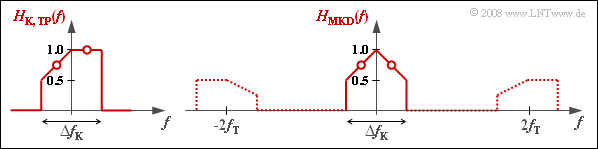
The resulting transmission function $H_{\rm MKD}(f)$ should not be confused with the low-pass transmission function $H_{\rm K, \, TP}(f)$ as described in the chapter "Equivalent Low-Pass Signal and its Spectral Function" of the book "Signal Representation", which results from $H_{\rm K}(f)$ by truncating the components at negative frequencies as well as a frequency shift by the carrier frequency $f_{\rm T}$ to the left.

For frequency responses, in contrast to spectral functions, the doubling of the components at positive frequencies must be omitted.

Notes:

The exercise belongs to the chapter "Linear Digital Modulation - Coherent Demodulation".

Reference is made in particular to the section "Baseband model for ASK and BPSK".

The subscript "MKD" stands for "modulator – channel – demodulator" German: "Modulator – Kanal – Demodulator").

Questions

Solution

(1) Statements 2, 3 and 4 are correct:

$H_{\rm K,TP}(f)$ results from $H_{\rm K}(f)$ by cutting off the negative frequency components and shifting $f_{\rm T}$ to the left.

For frequency responses – in contrast to spectra – the doubling of the components at positive frequencies is omitted. Therefore:

$$H_{\rm K,\hspace{0.04cm} TP}(f= 0) = H_{\rm K}(f= f_{\rm T})=1.$$

Because of the real and asymmetrical spectral functions $H_{\rm K,\hspace{0.04cm}TP}(f),$ the corresponding time function (inverse Fourier transform) $h_{\rm K,\hspace{0.04cm}TP}(t)$ is complex according to the "Allocation Theorem".

Low-pass functions for $H_{\rm K}(f)$

(2) Here only the third proposed solution is correct:

The spectral function $H_{\rm MKD}(f)$ always has an even real part and no imaginary part. Consequently $h_{\rm MKD}(t)$ is always real.

If $H_{\rm K}(f)$ had additionally an imaginary part odd by $f= f_{\rm T}$, $H_{\rm MKD}(f)$ would have an imaginary part odd by $f = 0$. Thus $h_{\rm MKD}(t)$ would still be a real function.

The diagram illustrates the differences between $H_{\rm K,\hspace{0.04cm}TP}(f)$ and $H_{\rm MKD}(f)$. The parts of $H_{\rm MKD}(f)$ in the range around $\pm 2f_{\rm T}$ need not be considered further.

(3) $H_{\rm MKD}(f)$ is additively composed of a rectangle and a triangle, each with width $\Delta f_{\rm K}$ and height $0.5$. It follows:

$$h_{\rm MKD}(t) = \frac{\Delta f_{\rm K}}{2} \cdot {\rm sinc} ( \Delta f_{\rm K} \cdot t)+ \frac{\Delta f_{\rm K}}{4} \cdot {\rm sinc}^2 ( \frac{\Delta f_{\rm K}}{2} \cdot t)$$

$$ \Rightarrow \hspace{0.3cm}h_{\rm MKD}(t = 0) = \frac{\Delta f_{\rm K}}{2} + \frac{\Delta f_{\rm K}}{4} = 0.75 \cdot \Delta f_{\rm K}\hspace{0.3cm} \Rightarrow \hspace{0.3cm}h_{\rm MKD}(t = 0)/{\Delta f_{\rm K}} \hspace{0.1cm}\underline {= 0.75} .$$

(4) The second proposed solution is correct:

The first sinc–function does have equidistant zero crossings at the distance $1/\Delta f_{\rm K}$.
But the equidistant zero crossings of the whole time function $h_{\rm MKD}(t)$ are determined by the second term:

$$h_{\rm MKD}(t = \frac{1}{\Delta f_{\rm K}}) = \ \frac{\Delta f_{\rm K}}{2} \cdot {\rm sinc} (1 )+ \frac{\Delta f_{\rm K}}{4} \cdot {\rm sinc}^2 (0.5) = \frac{\Delta f_{\rm K}}{4},$$

$$h_{\rm MKD}(t = \frac{2}{\Delta f_{\rm K}}) = \ \frac{\Delta f_{\rm K}}{2} \cdot {\rm sinc} (2 )+ \frac{\Delta f_{\rm K}}{4} \cdot {\rm sinc}^2 (1) = 0.$$

	$H_{\rm K, \, TP}(f=0)= 2$.
	$H_{\rm K, \, TP}(f = \Delta f_{\rm K}/4) = 1$.
	$H_{\rm K, \, TP}(f = -\Delta f_{\rm K}/4) = 0.75$.
	The corresponding time function $h_{\rm K, \, TP}(t)$ is complex.

	$H_{\rm MKD}(f=0)= 2$.
	$H_{\rm MKD}(f = \Delta f_{\rm K}/4) = 1$.
	$H_{\rm MKD}(f = -\Delta f_{\rm K}/4) = 0.75$.
	The corresponding time function $h_{\rm MKD}(t)$ is complex.

	$h_{\rm MKD}(t)$ has equidistant zero crossings at distance $1/\Delta f_{\rm K}$.
	$h_{\rm MKD}(t)$ has equidistant zero crossings at distance $2/\Delta f_{\rm K}$.