Exercise 3.1: Causality Considerations

• Return to book

Two two-port networks

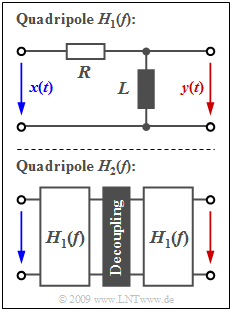
The graph shows above the two-port network with the transfer function

$$H_1(f) = \frac{{\rm j}\cdot f/f_{\rm G}}{1+{\rm j}\cdot f/f_{\rm G}} \hspace{0.05cm},$$

where  $f_{\rm G}$  represents the  $\rm 3dB$  cut-off frequency:

$$f_{\rm G} = \frac{R}{2 \pi \cdot L} \hspace{0.05cm}.$$

By cascading  $n$  two-port networks  $H_1(f)$  built in the same way, the following transfer function is obtained:

$$H_n(f) = \big [H_1(f)\big ]^n =\frac{\big [{\rm j}\cdot f/f_{\rm G}\big ]^n}{\big [1+{\rm j}\cdot f/f_{\rm G}\big ]^n} \hspace{0.05cm}.$$

• Here, a suitable resistor decoupling is presumed,  but this is not important for solving this exercise.
• The lower graph shows for example the realization of the transfer function  $H_2(f)$.

In this exercise,  such a two-port network is considered with respect to its causality properties.

For any causal system,  the real and imaginary parts of the spectral function  $H(f)$  satisfy the  Hilbert transformation,  which is expressed by the following abbreviation:

$${\rm Im} \left\{ H(f) \right \} \quad \bullet\!\!-\!\!\!-\!\!\!-\!\!\hspace{-0.05cm}\rightarrow\quad {\rm Re} \left\{ H(f) \right \}\hspace{0.05cm}.$$

Since the Hilbert transformation provides important information not only for transfer functions but also for time signals,  the correspondence is often expressed by the general variable  $x$,  which is to be interpreted - depending on the application - as normalized frequency or as normalized time.

Please note:

• The exercise belongs to the chapter  Conclusions from the Allocation Theorem.
• Reference is also made to the theory pages  Hilbert transformation  and  Partial fraction decomposition.

Questions

1

How can  $H_1(f)$  be characterized?

	$H_1(f)$  describes a low-pass filter.
	$H_1(f)$  describes a high-pass filter.

2

Does  $H_1(f)$  describe a causal network?

	Yes.
	No.

3

Compute the transfer function  $H_2(f)$.   What is the complex value for  $f = f_{\rm G}$?

${\rm Re}\big[H_2(f = f_{\rm G})\big] \ = \ $

${\rm Im}\big[H_2(f = f_{\rm G})\big] \ = \ $

4

Which of the following statements are true?

	$H_2(f)$  describes a causal system.
	The expressions  $(x^4 - x^2)/(x^4 +2 x^2 + 1)$  and  $2x^3/(x^4 +2 x^2 + 1)$  are a Hilbert pair.
	The causality condition is not satisfied for  $n > 2$ .

Solution

Solution

(1)  Proposed solution 2  is correct:

• The given transfer function can be computed according to the voltage divider principle.   The following holds:

$$H_1(f = 0) = 0, \hspace{0.2cm}H_1(f \rightarrow \infty) = 1$$

• This is a high-pass filter.
• For very low frequencies, the inductivity  $L$  constitutes a short circuit.

(2)  Yes  is correct:

• Every real network is causal.  The impulse response  $h(t)$  is equal to the output signal  $y(t)$  if at time  $t= 0$  an extremely short impulse – a so-called Dirac delta impulse – is applied to the input.
• Then,  a signal cannot occur at the output already for times  $t< 0$  for causality reasons:

$$y(t) = h(t) = 0 \hspace{0.2cm}{\rm{f\ddot{u}r}} \hspace{0.2cm} t<0 \hspace{0.05cm}.$$

• Formally, this can be shown as follows:   The high-pass transfer function  $H_1(f)$  can be rearranged as follows:

$$H_1(f) = \frac{{\rm j}\cdot f/f_{\rm G}}{1+{\rm j}\cdot f/f_{\rm G}} = 1- \frac{1}{1+{\rm j}\cdot f/f_{\rm G}} \hspace{0.05cm}.$$

• The second transfer function describes the low-pass function equivalent to  $H_1(f)$,  which results in the exponential function in the time domain.
• The  "$1$"  becomes a Dirac delta function.  Considering  $T = 2\pi \cdot f_{\rm G}$  the following thus holds for  $t \ge 0$:

$$h_1(t) = \delta(t) - {1}/{T} \cdot {\rm e}^{-t/T} \hspace{0.05cm}.$$

• In contrast,  $h_1(t)= 0$ holds for  $t< 0$,  which would prove causality.

(3)  The series connection of two high-pass filters results in the following transfer function:

$$H_2(f) = \big [H_1(f)\big ]^2 =\frac{\big [{\rm j}\cdot f/f_{\rm G}\big ]^2}{\big [1+{\rm j}\cdot f/f_{\rm G}\big ]^2} =\frac{\big [{\rm j}\cdot f/f_{\rm G}\big ]^2 \cdot \big [(1-{\rm j}\cdot f/f_{\rm G})\big ]^2} {\big [(1+{\rm j}\cdot f/f_{\rm G}) \cdot (1-{\rm j}\cdot f/f_{\rm G})\big ]^2}= \frac{(f/f_{\rm G})^4 - (f/f_{\rm G})^2 +{\rm j}\cdot 2 \cdot (f/f_{\rm G})^3)} {\big [1+(f/f_{\rm G})^2 \big ]^2}\hspace{0.05cm}.$$

• With  $f = f_{\rm G}$  from this it follows that:

$$H_2(f = f_{\rm G}) = \frac{1 - 1 +{\rm j}\cdot 2} {4}= {\rm j} /{2} \hspace{0.5cm}\Rightarrow \hspace{0.5cm}{\rm Re} \left\{ H_2(f = f_{\rm G}) \right \} \hspace{0.15cm}\underline{ = 0}, \hspace{0.4cm} {\rm Im} \left\{ H_2(f = f_{\rm G}) \right \} \hspace{0.15cm}\underline{ = 0.5}\hspace{0.05cm}.$$

(4)  The first two proposed solutions  are correct:

• Since the impulse response is  $h_1(t) = 0$  for  $t < 0$,  the convolution operation  $h_2(t) = h_1(t) \star h_1(t)$  also satisfies the causality condition. 
• Similarly, the  $n$–fold convolution yields a causal impulse response:   $h_n(t) = 0 \hspace{0.2cm}{\rm{for}} \hspace{0.2cm} t<0 \hspace{0.05cm}.$
• However,  the real and imaginary parts of the spectral function  $H_2(f)$  are related via the Hilbert transformation for a causal impulse response  $h_2(t)$ . 
• Thus,  considering the shortcut  $x = f/f_{\rm G}$  and the result of the subtask  (3)  the following holds:

$$\frac{x^4- x^2}{x^4+2 x^2+1} \quad \bullet\!\!-\!\!\!-\!\!\!-\!\!\hspace{-0.05cm}\rightarrow\quad \frac{2x^3}{x^4+2 x^2+1}\hspace{0.05cm}.$$