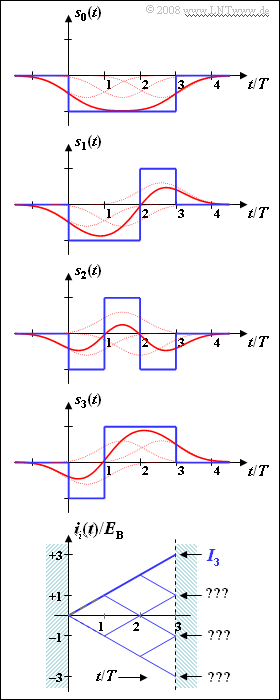
Exercise 3.10: Maximum Likelihood Tree Diagram

• Return to book

Signals and tree diagram

As in  "Exercise 3.9"  we consider the joint decision of three binary symbols  ("bits")  by means of the correlation receiver.

• The possible transmitted signals  $s_0(t), \ \text{...} \ , \ s_7(t)$  are bipolar.

• In the graphic the functions  $s_0(t)$,  $s_1(t)$,  $s_2(t)$  and  $s_3(t)$  are shown.

• The blue curves are valid for rectangular NRZ transmission pulses.

Below is drawn the so-called  "tree diagram"  for this constellation under the condition that the signal  $s_3(t)$  was sent.  Shown here in the range from  $0$  to  $3T$  are the functions

$$i_i(t) = \int_{0}^{t} s_3(\tau) \cdot s_i(\tau) \,{\rm d} \tau \hspace{0.3cm}( i = 0, \ \text{...} \ , 7)\hspace{0.05cm}.$$

• The correlation receiver compares the final values  $I_i = i_i(3T)$  with each other and searches for the largest possible value  $I_j$.

• The corresponding signal  $s_j(t)$  is then the one most likely to have been sent according to the maximum likelihood criterion.

• Note that the correlation receiver generally makes the decision based on the corrected quantities  

$$W_i = I_i \ - E_i/2.$$

• But since for bipolar rectangles all transmitted signals  $(i = 0, \ \text{...} \ , \ 7)$  have exactly the same energy

$$E_i = \int_{0}^{3T} s_i^2(t) \,{\rm d} t,$$

the integrals  $I_i$  provide exactly the same maximum likelihood information as the corrected quantities  $W_i$.

The red signal waveforms  $s_i(t)$  are obtained from the blue ones by convolution with the impulse response  $h_{\rm G}(t)$  of a Gaussian low-pass filter with cutoff frequency  $f_{\rm G} \cdot T = 0.35$.

• Each individual rectangular pulse is broadened.

• The red signal waveforms lead to  "intersymbol interference"  in case of threshold decision.

Note:  The exercise belongs to the chapter  "Optimal Receiver Strategies".

Questions

1

Give the following normalized final values  $I_i/E_{\rm B}$  for rectangular signals  $($without noise$)$.

$I_0/E_{\rm B} \ = \ $

$I_2/E_{\rm B} \ = \ $

$I_4/E_{\rm B} \ = \ $

$I_6/E_{\rm B} \ = \ $

2

Which statements are valid when considering a noise term?

	The tree diagram can be further described by straight line segments.
	If  $I_3$  is the maximum  $I_i$  value,  the receiver decides correctly.
	$I_0 = I_6$  is valid independent of the strength of the noise.

3

Which statements are valid for the red signal waveforms  $($with intersymbol interference$)$?

	The tree diagram can be further described by straight line segments.
	The signal energies  $E_i(i = 0, \ \text{...} \ , 7$)  are different.
	Both the decision variables  $I_i$  and  $W_i$  are suitable.

4

How should the intergration range  $(t_1 \ \text{...} \ t_2)$  be chosen?

	Without intersymbol interference (blue),  $t_1 = 0$  and  $t_2 = 3T$  are best possible.
	With intersymbol interference (red),  $t_1 = 0$  and  $t_2 = 3T$  are best possible.

Solution

Solution

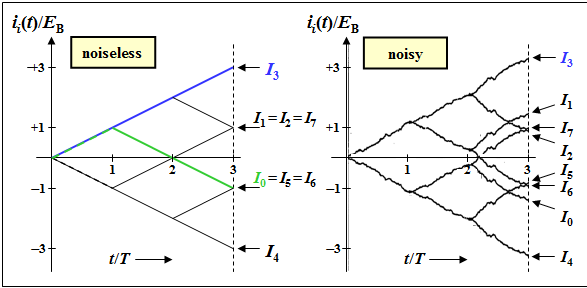
(1)  The left graph shows the tree diagram  (without noise)  with all final values.  Highlighted in green is the curve  $i_0(t)/E_{\rm B}$  with the final result  $I_0/E_{\rm B} = \ -1$,  which first rises linearly to  $+1$  $($the first bit of  $s_0(t)$  and  $s_3(t)$  in each case coincide$)$  and then falls off over two bit durations.

Tree diagram of the correlation receiver

• The correct results are thus:

$$I_0/E_{\rm B}\hspace{0.15cm}\underline { = -1},$$

$$I_2/E_{\rm B} \hspace{0.15cm}\underline {= +1},$$

$$I_4/E_{\rm B} \hspace{0.15cm}\underline {= -3},$$

$$I_6/E_{\rm B}\hspace{0.15cm}\underline { = -1} \hspace{0.05cm}.$$

(2)  Only the  second solution  is correct:

• In the presence of noises,  the functions  $i_i(t)$  no longer increase or decrease linearly,  but have a curve as shown in the right graph.
• As long as  $I_3 > I_{\it i≠3}$,  the correlation receiver decides correctly.
• In the presence of noise,  $I_0 ≠ I_6$  always holds,  in contrast to the noise-free tree diagram.

(3)  Only the  second statement  is true:

• Since now the possible transmitted signals  $s_i(t)$  can no longer be composed of isolated horizontal sections,  also the tree diagram without noise does not consist of straight line segments.
• Since the energies  $E_i$  are different – this can be seen e.g. by comparing the  (red)  signals  $s_0(t)$  and  $s_2(t)$  – it is essential to use the corrected quantities  $W_i$  for the decision.
• The use of the uncorrected correlation values  $I_i$  can already lead to wrong decisions without noise disturbances.

(4)  Answer 1  is correct:

• In the case  without intersymbol interference  (blue rectangular signals),  all signals are limited to the range  $0 \ ... \ 3T$.
• Outside this range the received signal  $r(t)$  is pure noise.  Therefore in this case also the integration over the range  $0 \ \text{...} \ 3T$.
• In contrast,  when intersymbol interference  (red signals)  is taken into account,  the integrands  $s_3(t) \cdot s_i(t)$  also differ outside this range.
• Therefore,  if  $t_1 = \ -T$  and  $t_2 = +4T$  are chosen,  the error probability of the correlation receiver is further reduced compared to the integration range  $0 \ \text{...} \ 3T$.