Exercise 5.6: Filter Dimensioning

• Return to book

Desired ACF  $\varphi_y(k \cdot T_{\rm A})$

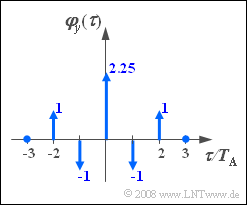
A discrete-time random variable  $\left\langle \hspace{0.05cm}{y_\nu } \hspace{0.05cm}\right\rangle$  with the outlined auto-correlation function  $\rm (ACF)$  is to be generated using a digital filter.

Let the discrete-time Gaussian input values  $x_\nu$  be characterized in each case by

• the mean value  $m_x = 0$,
• the standard deviation  $\sigma_x = 1$.

Notes:

• The exercise belongs to the chapter  Creation of Predefined ACF Properties.
• Reference is also made to the chapter  Auto-Correlation Function.
• Let all ACF values  $\varphi_y(k \cdot T_{\rm A})$  with index  $|k| \gt 2$  be zero.

Questions

1

Which of the following statements are true?

	A first-order recursive filter is suitable.
	A first-order non-recursive filter is suitable.
	A second order non-recursive filter is suitable.
	The output values  $y_\nu$  are triangularly distributed.
	The output values  $y_\nu$  are mean-free  $(m_y = 0)$.

2

Give the equations for determining the coefficients  $a_0$,  $a_1$  and  $a_2$.    Replace the three variables with  $u = a_1^2$  and  $w = (a_0 + a_2)^2$.  Determine  $u$  and  $w$. 
      Note:  There is only one reasonable solution.

$u \ = \ $

$w \ = \ $

3

Determine the filter coefficients  $a_0$,  $a_1$  and  $a_2$.  Enter the following quotients:

$a_1/a_0 \ = \ $

$a_2/a_0 \ = \ $

4

How many different sets of parameters  $(I)$  lead to the desired ACF?

$I \ = \ $

Solution

Solution

(1)  Solutions 3 and 5  are correct:

• A recursive filter would always cause an infinitely extended impulse response  $h(t)$  and thus also an infinitely extended auto-correlation function  $\rm (ACF)$.
• Therefore,  a non-recursive filter structure must be chosen here.  The specified ACF requires the order  $M= 2$.
• Since the input values are Gaussian distributed and mean-free,  this also applies to the output values.
• When filtering stochastic signals,  the following always applies:  Gaussian remains Gaussian and non-Gaussian never becomes (exactly) Gaussian.

(2)  The system of equations is:

$$k = 2\text{:}\quad a_0 \cdot a_2 = 1.$$

$$k = 1\text{:}\quad a_0 \cdot a_1 + a_1 \cdot a_2 = - 1\quad \Rightarrow \quad \sqrt {u \cdot w} = - 1\quad \Rightarrow \quad u \cdot w = 1.$$

$$k = 0\text{:}\quad a_0 ^2 + a_1 ^2 + a_2 ^2 = 2.25\quad \;\;\, \Rightarrow \quad u + w = 2.25 + 2a_0 \cdot a_2 = 4.25.$$

The two equations with respect to  $u$  and  $w$  has two solutions:

• $u = 4, \ w = 0.25$:   Because of the condition  $a_2 = 1/a_0$  (see first equation),  $a_0$  and  $a_2$  have the same sign.
• Moreover,  at least one of the two coefficients is greater than/equal to  $1$.
• Thus the condition  $a_0+a_2= \sqrt{w} = 0.5$  cannot be fulfilled.
• Therefore,  the correct solution is  $\underline{u = 0.25}, \ \underline{w = 4}$.

(3)  The result of  (2)  means that  $a_1 = \pm \sqrt{0.25} = \pm 0.5$. 

• The positive value leads to the equations

$$(1) \hspace{0.5cm}0.5 \cdot \left( {a_0 + a_2 } \right) = - 1\quad \Rightarrow \quad a_0 + a_2 = - 2,$$

$$(2) \hspace{0.5cm}a_0 \cdot a_2 = 1.$$

• From this follows  $a_0=a_2=-1$.  With  $a_1= 0.5$,  the final result is:

$$a_1/a_0 \hspace{0.15 cm}\underline{= -0.5}, \hspace{0.5 cm} a_2/a_0 \hspace{0.15 cm}\underline{= 1}.$$

• The solution  $a_1= -0.5$  leads to  $a_0=a_2=+1$  and thus to the same quotients.

(4)  In general,  this problem has  $I = 4$  equivalent solutions  $($mirroring/shifting as well as the multiplication by  $-1$  in each case$)$.

• Since here the impulse response is symmetrical,  there are however only  $\underline{I = 2}$  different solutions:

$$\text{Solution 1:} \ \ a_0 = +1,\quad a_1 = - 0.5,\quad a_2 = +1; $$

$$\text{Solution 2:} \ \ a_0 = - 1,\quad a_1 = +0.5,\quad a_2 = - 1. $$