Difference between revisions of "Applets:Zur Verdeutlichung des Matched-Filters"
m (Text replacement - "„" to """) |
|||
| (31 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{LntAppletLink| | + | {{LntAppletLink|sampling}} |
| − | == | + | == Applet Description== |
<br> | <br> | ||
| − | Das Applet | + | Das Applet soll die Eigenschaften des so genannten "Matched-Filters" $({\rm MF})$ verdeutlichen. Dieses dient zur optimalen Bestimmung des Vorhandenseins (Detektion) der Amplitude und/oder der Lage einer bekannten Signalform in einer stark verrauschten Umgebung. Oder allgemeiner gesprochen: Das Matched-Filter – manchmal auch als "Optimalfilter" oder als "Korrelationsfilter" bezeichnet – dient dem Nachweis der Signalexistenz. |
| − | [[File: | + | [[File:P_ID568__Sto_T_5_4_S1_neu.png |right|frame| Blockschaltbild des Matched-Filter-Empfängers]] |
| − | |||
| − | |||
| − | |||
| + | Die Grafik zeigt den so genannten '''Matched-Filter-Empfänger''': | ||
| − | + | *Dieser kann mit größtmöglicher Sicherheit – anders ausgedrückt: mit maximalem Signal–zu–Rausch–Verhältnis $($englisch: signal–to–noise–ratio, $\rm SNR)$ – entscheiden, ob ein durch additives Rauschen $n(t)$ gestörtes impulsförmiges Nutzsignal $g(t)$ vorhanden ist oder nicht. | |
| + | *Eine Anwendung ist die Radartechnik, bei der man zwar die Impulsform $g(t)$ kennt, nicht aber, wann der Impuls gesendet wurde und mit welcher Stärke und Verzögerung dieser ankommt. | ||
| + | *Das Matched-Filter wird aber auch als Empfangsfilter in digitalen Übertragungssystemen (oder zumindest als Teil davon) eingesetzt, um die Fehlerwahrscheinlichkeit des Systems zu minimieren. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| + | Alle Parameter, Zeiten und Frequenzen sind als normierte Größen zu verstehen und damit dimensionslos. | ||
| − | + | * Für den '''Eingangsimpuls''' $g(t)$ sind "Rechteck", "Gauß" und "Exponential" einstellbar, die jeweils durch die Impulsamplitude $A_g$, die äquivalente Impulsdauer $\Delta t_g$ sowie die Verschiebung $\tau_g$ gegenüber dem (hinsichtlich Zeit) symmetrischen Fall beschrieben werden. Weitere Informationen im Abschnitt [[Applets:Zur_Verdeutlichung_des_Matched-Filters#Weitere_Angaben_zu_den_betrachteten_Eingangsimpulsen|Weitere Angaben zu den betrachteten Eingangsimpulsen]]. | |
| + | * Für das '''Empfangsfilter''' kann zwischen den Alternativen "Spalt–Tiefpass", "Gauß–Tiefpass", "Tiefpass erster Ordnung"und "Tiefpass 4" gewählt werden. Dargestellt werden die jeweiligen Impulsantworten $h(t)$, gekennzeichnet durch deren Höhe $A_h$, die äquivalente Dauer $\Delta t_h$ und die Verschiebung $\tau_h$. Weitere Informationen im Abschnitt [[Applets:Zur_Verdeutlichung_des_Matched-Filters#Weitere_Angaben_zu_den_betrachteten_Impulsantworten|Weitere Angaben zu den betrachteten Impulsantworten]]. | ||
| + | * Weitere Eingabeparameter sind der Detektionszeitpunkt $T_{\rm D}$ sowie die ebenfalls normierte Rauschleistungsdichte $N_0$ am Empfängereingang. | ||
| − | |||
| − | + | Als Numerikwerte ausgegeben werden | |
| − | + | *die Energie $E_g$ des Eingangsimpulses $g(t)$, der Nutzabtastwert $d_{\rm S} (T_{\rm D})$ am Filterausgang sowie die Rauschvarianz $\sigma_d^2$ am Filterausgang, | |
| + | *das Signal–zu–Rausch–Verhältnis $\rm (SNR)$ $\rho_{d} (T_{\rm D})$ am Filterausgang und die zugehörige dB–Angabe $10 \cdot \lg \ \rho_{d} (T_{\rm D})$, | ||
| + | *der hierfür maximale Wert $10 \cdot \lg \ \rho_{\rm MF}$. | ||
| − | |||
| − | + | Erfüllt die eingegebene Konfiguration die Matched-Filter-Bedingungen, dann gilt: $10 \cdot \lg \ \rho_{d} (T_{\rm D,\ opt}) = 10 \cdot \lg \ \rho_{\rm MF}$. | |
| − | |||
| − | |||
| − | + | ==Theoretical Background== | |
| + | <br> | ||
| + | ===Detailbeschreibung des zugrunde liegenden Modells=== | ||
| − | '''( | + | Für die einzelnen Komponenten des obigen Blockschaltbild gelten folgende Voraussetzungen: |
| + | *Der Nutzanteil $g(t)$ des Empfangssignals $r(t)=g(t)+n(t)$ sei impulsförmig und somit ''energiebegrenzt''. Das heißt: Das Integral über $ [g(t) ]^2$ von $–∞$ bis $+∞$ liefert den endlichen Wert $E_g$. | ||
| + | *Das Störsignal $n(t)$ sei ''Weißes Gaußsches Rauschen'' mit der Rauschleistungsdichte $N_0$. | ||
| + | *Das Filterausgangssignal $d(t)= d_{\rm S}(t) + d_{\rm N}(t)$ besteht additiv aus zwei Anteilen. Der Anteil $d_{\rm S}(t)$ geht auf das $\rm S\hspace{0.04cm}$ignal $g(t)$ zurück, $d_{\rm N}(t)$ auf das $\rm N\hspace{0.04cm}$oise $n(t)$. | ||
| + | *Der Empfänger, bestehend aus einem linearen Filter ⇒ Frequenzgang $H_{\rm MF}(f)$ und dem Entscheider, ist so zu dimensionieren, dass das momentane S/N-Verhältnis am Ausgang maximal wird: | ||
| + | :$$\rho _d ( {T_{\rm D} } ) = \frac{ {d_{\rm S} ^2 ( {T_{\rm D} } )} }{ {\sigma_d^2 } }\mathop = \limits^{\rm{!} }\hspace{0.1cm} {\rm{Maximum} }.$$ | ||
| + | *Hierbei bezeichnen ${σ_d}^2$ die ''Varianz'' (Leistung) von $d_{\rm N}(t)$ und $T_{\rm D}$ den (geeignet gewählten) ''Detektionszeitpunkt.'' | ||
| − | |||
| − | + | ===Matched-Filter-Optimierung=== | |
| − | + | Gegeben sei ein energiebegrenztes Nutzsignal $g(t)$ mit dem zugehörigen Spektrum $G(f)$. Damit kann das Filterausgangssignal zum Detektionszeitpunkt $T_{\rm D}$ für jedes beliebige Filter mit Impulsantwort $h(t)$ und Frequenzgang $H(f) =\mathcal{ F}\{h(t)\}$ geschrieben werden (ohne Berücksichtigung des Rauschens ⇒ Index $\rm S$ für „Signal”): | |
| + | :$$d_{\rm S} ( {T_{\rm D} } ) = g(t) * h(t) = \int_{ - \infty }^{ + \infty } {G(f) \cdot H(f) \cdot {\rm{e}}^{ {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f \hspace{0.05cm}\cdot \hspace{0.05cm}T_{\rm D} }\hspace{0.1cm} {\rm{d}}f} .$$ | ||
| − | :$$ | + | Der „Rauschanteil” $d_{\rm N}(t)$ des Filterausgangssignals (Index $\rm N$ für „Noise”) rührt allein vom Weißen Rauschen $n(t)$ am Eingang des Empfängers her. Für seine Varianz (Leistung) gilt unabhängig vom Detektionszeitpunkt $T_{\rm D}$: |
| + | :$$\sigma _d ^2 = \frac{ {N_0 } }{2} \cdot \int_{ - \infty }^{ + \infty } {\left| {H(f)} \right|^{\rm{2} }\hspace{0.1cm} {\rm{d} }f} .$$ | ||
| + | Damit lautet das hier vorliegende Optimierungsproblem: | ||
| + | :$$\rho _d ( {T_{\rm D} } ) = \frac{ {\left| {\int_{ - \infty }^{ + \infty } {G(f) \cdot H(f) \cdot {\rm{e} }^{ {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f \hspace{0.05cm}\cdot \hspace{0.05cm}T_{\rm D} }\hspace{0.1cm} {\rm{d} }f} } \right|^2 } }{ {N_0 /2 \cdot \int_{ - \infty }^{ + \infty } {\left| {H(f)} \right|^{\rm{2} }\hspace{0.1cm} {\rm{d} }f} } } \stackrel{!}{=} {\rm{Maximum} }.$$ | ||
| + | {{BlaueBox|TEXT= | ||
| + | Dieser Quotient wird für den folgenden Frequenzgang $H(f)$ am größten wird: | ||
| + | :$$H(f) = H_{\rm MF} (f) = K_{\rm MF} \cdot G^{\star} (f) \cdot {\rm e}^{- {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f \hspace{0.05cm}\cdot \hspace{0.05cm}T_{\rm D} } . $$ | ||
| + | *Damit erhält man für das Signal–zu–Rauschleistungsverhältnis am Matched–Filter–Ausgang $($unabhängig von der dimensionsbehafteten Konstante $K_{\rm MF})$: | ||
| + | :$$\rho _d ( {T_{\rm D} } ) = { {2 \cdot E_g } }/{ {N_0 } } \hspace{0.5cm}\Rightarrow \hspace{0.5cm} \rho _{\rm MF}.$$ | ||
| + | * $E_g$ bezeichnet die Energie des Eingangsimpulses, die man nach dem [https://de.wikipedia.org/wiki/Satz_von_Parseval Satz von Parseval] sowohl im Zeit– als auch im Frequenzbereich berechnen kann: | ||
| + | :$$E_g = \int_{ - \infty }^{ + \infty } {g^2 (t)\hspace{0.1cm}{\rm{d} }t} = \int_{ - \infty }^{ + \infty } {\left \vert {G(f)} \right\vert ^{\rm{2} }\hspace{0.1cm} {\rm d}f} .$$}} | ||
| + | {{BlaueBox|TEXT= | ||
| + | $\text{Herleitung des Matched–Filter–Kriteriums:}$ | ||
| + | $(1)$ Die Schwarzsche Ungleichung lautet mit den beiden (im allgemeinen komplexen) Funktionen $A(f)$ und $B(f)$: | ||
| + | :$$\left \vert {\int_a^b {A(f) \cdot B(f)\hspace{0.1cm}{\rm{d} }f} } \right \vert ^2 \le \int_a^b {\left \vert {A(f)} \right \vert^{\rm{2} } \hspace{0.1cm}{\rm{d} }f} \cdot \int_a^b {\left\vert {B(f)} \right \vert^{\rm{2} } \hspace{0.1cm}{\rm{d} }f} .$$ | ||
| + | $(2)$ Wir wenden nun diese Gleichung auf das Signal–zu–Rauschverhältnis an: | ||
| + | :$$\rho _d ( {T_{\rm D} } ) = \frac{ {\left \vert {\int_{ - \infty }^{ + \infty } {G(f) \cdot H(f) \cdot {\rm{e} }^{ {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f \hspace{0.05cm}\cdot \hspace{0.05cm}T_{\rm D} } \hspace{0.1cm}{\rm{d} }f} } \right \vert^2 } }{ {N_0 /2 \cdot \int_{ - \infty }^{ + \infty } {\left \vert {H(f)} \right \vert^{\rm{2} }\hspace{0.1cm} {\rm{d} }f} } }.$$ | ||
| + | $(3)$ Mit $A(f) = G(f)$ und $B(f) = H(f) · {\rm e}^{ {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f \hspace{0.05cm}\cdot \hspace{0.05cm}T_{\rm D} }$ ergibt sich somit die folgende Schranke: | ||
| + | :$$\rho_d ( {T_{\rm D} } ) \le \frac{1}{ {N_0 /2} } \cdot \int_{ - \infty }^{ + \infty } {\left \vert {G(f)} \right \vert^{\rm{2} } }\hspace{0.1cm}{\rm{d} }f .$$ | ||
| + | $(4)$ Wir setzen für den Filterfrequenzgang nun versuchsweise ein: | ||
| + | :$$H(f) = H_{\rm MF} (f) = K_{\rm MF} \cdot G^{\star} (f) \cdot {\rm{e} }^{- {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f \hspace{0.05cm}\cdot \hspace{0.05cm}T_{\rm D} }.$$ | ||
| + | $(5)$ Dann erhält man aus der obigen Gleichung $(2)$ folgendes Ergebnis: | ||
| + | :$$\rho _d ( {T_{\rm D} } ) = \frac{ {\left \vert K_{\rm MF}\cdot {\int_{ - \infty }^{ + \infty } {\left \vert {G(f)} \right \vert ^{\rm{2} }\hspace{0.1cm} {\rm{d} }f} } \right \vert ^2 } }{ {N_0 /2 \cdot K_{\rm MF} ^2 \cdot \int_{ - \infty }^{ + \infty } {\left \vert {G(f)} \right \vert ^{\rm{2} }\hspace{0.1cm} {\rm{d} }f} } } = \frac{1}{ {N_0 /2} } \cdot \int_{ - \infty }^{ + \infty } {\left \vert {G(f)} \right \vert ^{\rm{2} }\hspace{0.1cm} {\rm{d} }f} .$$ | ||
| − | + | $\text{Das heißt:}$ | |
| − | = | + | *Mit dem Ansatz $(4)$ für das Matched–Filter $H_{\rm MF}(f)$ wird in obiger Abschätzung tatsächlich der maximal mögliche Wert erreicht. |
| + | *Mit keinem anderen Filter $H(f) ≠ H_{\rm MF}(f)$ kann man ein höheres Signal–zu–Rauschleistungsverhältnis erzielen. | ||
| + | *Das Matched–Filter ist in Bezug auf das ihm zugrunde gelegte Maximierungskriterium optimal. | ||
| + | <div align="right">'''q.e.d.'''</div> | ||
| + | }} | ||
| − | === | + | {{GraueBox|TEXT= |
| + | $\text{Beispiel 1:}$ Ein rechteckförmiger Impuls $g(t)$ mit Amplitude $\rm 1\hspace{0.05cm}V$, Dauer $0.5\hspace{0.05cm} \rm ms$ und unbekannter Lage soll in einer verrauschten Umgebung aufgefunden werden. | ||
| + | *Somit ist die Impulsenergie $E_g = \rm 5 · 10^{–4} \hspace{0.05cm}V^2s$. | ||
| + | *Die Rauschleistungsdichte sei $N_0 = \rm 10^{–6} \hspace{0.05cm}V^2/Hz$. | ||
| − | |||
| − | + | Das beste Ergebnis ⇒ das '''maximale S/N–Verhältnis''' erzielt man mit dem Matched-Filter: | |
| − | + | :$$\rho _d ( {T_{\rm D} } ) = \frac{ {2 \cdot E_g } }{ {N_0 } } = | |
| − | + | \frac{ {2 \cdot 5 \cdot 10^{-4}\, {\rm V^2\,s} } }{ {10^{-6}\, {\rm V^2/Hz} } } = 1000 | |
| − | + | \hspace{0.3cm}\Rightarrow\hspace{0.3cm} | |
| − | + | 10 \cdot {\rm lg}\hspace{0.15cm}\rho _d ( {T_{\rm D} } ) = 30\,{\rm dB}= 10 \cdot {\rm lg}\hspace{0.15cm}\rho_{\rm MF}.$$}} | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ===Interpretation des Matched-Filters=== | |
| − | {{ | + | Auf der letzten Seite wurde der Frequenzgang des Matched-Filters wie folgt hergeleitet: |
| − | $\ | + | :$$H_{\rm MF} (f) = K_{\rm MF} \cdot G^{\star} (f) \cdot {\rm{e} }^{- {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f \hspace{0.05cm}\cdot \hspace{0.05cm}T_{\rm D} } .$$ |
| + | Durch [[Signal_Representation/Fourier_Transform_and_Its_Inverse#Das_zweite_Fourierintegral|Fourierrücktransformation]] erhält man die dazugehörige Impulsantwort: | ||
| + | :$$h_{\rm MF} (t) = K_{\rm MF} \cdot g(T_{\rm D} - t).$$ | ||
| − | * | + | Diese beiden Funktionen lassen sich wie folgt interpretieren: |
| + | *Das ''Matched-Filter'' ist durch den Term $G^{\star}(f)$ an das Spektrum des aufzufindenden Impulses $g(t)$ angepasst – daher sein Name (englisch: ''to match'' ≡ anpassen). | ||
| + | *Die ''Konstante'' $K_{\rm MF}$ ist aus Dimensionsgründen notwendig. | ||
| + | *Ist $g(t)$ ein Spannungsimpuls, so hat diese Konstante die Einheit „Hz/V”. Der Frequenzgang ist somit dimensionslos. | ||
| + | *Die ''Impulsantwort'' $h_{\rm MF}(t)$ ergibt sich aus dem Nutzsignal $g(t)$ durch Spiegelung ⇒ aus $g(t)$ wird $g(–t)$ sowie einer Verschiebung um $T_{\rm D}$ nach rechts. | ||
| + | *Der ''früheste Detektionszeitpunkt'' $T_{\rm D}$ folgt für realisierbare Systeme aus der Bedingung $h_{\rm MF}(t < 0)\equiv 0$ $($„Kausalität”, siehe Buch [[Lineare_zeitinvariante_Systeme|Lineare zeitinvariante Systeme]]$)$. | ||
| + | *Der ''Nutzanteil'' $d_{\rm S} (t)$ des Filterausgangssignals ist formgleich mit der [[Digital_Signal_Transmission/Grundlagen_der_codierten_Übertragung#AKF.E2.80.93Berechnung_eines_Digitalsignals|Energie-AKF]] $\varphi^{^{\bullet} }_{g} (t )$ und gegenüber dieser um $T_{\rm D}$ verschoben. Es gilt: | ||
| + | :$$d_{\rm S} (t) = g(t) * h_{\rm MF} (t) = K_{\rm MF} \cdot g(t) * g(T_{\rm D} - t) = K_{\rm MF} \cdot \varphi^{^{\bullet} }_{g} (t - T_{\rm D} ).$$ | ||
| − | :$$ | + | {{BlaueBox|TEXT= |
| + | $\text{Bitte beachten Sie:}$ | ||
| + | Bei einem energiebegrenzten Signal $g(t)$ kann man nur die ''Energie–AKF'' angeben: | ||
| + | :$$\varphi^{^{\bullet} }_g (\tau ) = \int_{ - \infty }^{ + \infty } {g(t) \cdot g(t + \tau )\,{\rm{d} }t} .$$ | ||
| + | Gegenüber der AKF-Definition eines leistungsbegrenzten Signals $x(t)$, nämlich | ||
| + | :$$\varphi _x (\tau ) = \mathop {\lim }_{T_{\rm M} \to \infty } \frac{1}{ {T_{\rm M} } }\int_{ - T_{\rm M} /2}^{+T_{\rm M} /2} {x(t) \cdot x(t + \tau )\hspace{0.1cm}\,{\rm{d} }t} ,$$ | ||
| + | wird bei der Berechnung der Energie-AKF auf die Division durch die Messdauer $T_{\rm M}$ sowie auf den Grenzübergang $T_{\rm M} → ∞$ verzichtet.}} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | {{GraueBox|TEXT= | |
| − | :$$ | + | $\text{Beispiel 2:}$ Wir gehen davon aus, dass der Rechteckimpuls zwischen $\rm 2\hspace{0.08cm}ms$ und $\rm 2.5\hspace{0.08cm}ms$ liegt und der Detektionszeitpunkt $T_{\rm D} =\rm 2\hspace{0.08cm}ms$ gewünscht wird. |
| − | |||
| − | |||
| − | * | + | Unter diesen Voraussetzungen gilt: |
| − | + | *Die Matched–Filter–Impulsantwort $h_{\rm MF}(t)$ muss im Bereich von $t_1 (= 4 - 2.5) =\rm 1.5\hspace{0.08cm}ms$ bis $t_2 (= 4 - 2) =\rm 2\hspace{0.08cm}ms$ konstant sein. | |
| − | * | + | *Für $t < t_1$ sowie für $t > t_2$ darf sie keine Anteile besitzen. |
| − | *Die | + | *Der Betragsfrequenzgang $\vert H_{\rm MF}(f)\vert$ ist hier $\rm si$–förmig. |
| − | + | *Die Höhe der Impulsantwort $h_{\rm MF}(t)$ spielt für das S/N–Verhältnis keine Rolle, da dieses unabhängig von $K_{\rm MF}$ ist.}} | |
| + | <br clear=all> | ||
| + | ===Weitere Angaben zu den betrachteten Eingangsimpulsen=== | ||
| + | Alle Angaben sind ohne Berücksichtigung der Verzögerung $\tau_g$ | ||
| − | + | '''(1) Rechteckimpuls''' ⇒ ''Rectangular Impulse'' | |
| + | *Der Impuls $g(t)$ hat im Bereich $\pm \Delta t_g/2$ die konstante Höhe $A_g$ und ist außerhalb Null. | ||
| + | *Die Spektralfunktion $G(f)=A_g\cdot \Delta t_g \cdot {\rm si}(\pi\cdot \Delta t_g \cdot f)$ besitzt Nullstellen in äquidistanten Abständen $1/\Delta t_g$. | ||
| + | *Die Impulsenergie ist $E_g=A_g^2\cdot \Delta t_g$. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | '''(2) Gaußimpuls''' ⇒ ''Gaussian Imulse'' | |
| − | + | *Der Impuls $g(t)=A_g\cdot {\rm e}^{-\pi\cdot(t/\Delta t_g)^2}$ ist unendlich weit ausgedehnt. Das Maximum ist $g(t= 0)=A_g$. | |
| − | + | *Je kleiner die äquivalente Zeitdauer $\Delta t_g$ ist, um so breiter und niedriger ist das Spektrum $G(f)=A_g \cdot \Delta t_g \cdot {\rm e}^{-\pi\hspace{0.05cm}\cdot\hspace{0.05cm}(f\hspace{0.05cm}\cdot\hspace{0.05cm} \Delta t_g)^2}$. | |
| − | + | *Die Impulsenergie ist $E_g=A_g^2\cdot \Delta t_g/\sqrt{2}$. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | '''(3) Exponentialimpuls''' ⇒ ''Exponential Impulse'' | ||
| + | *Der Impuls ist für $t<0$ identisch Null und für positive Zeiten unendlich weit ausgedehnt ⇒ $g(t)=A_g\cdot {\rm e}^{-t/\Delta t_g}$. | ||
| + | *$g(t)$ ist (stark) unsymmetrisch ⇒ das Spektrum $G(f)=A_g \cdot \Delta t_g/( 1 + {\rm j} \cdot 2\pi \cdot f \cdot \Delta t_g)$ ist komplexwertig; | ||
| + | *Die Impulsenergie ist $E_g=A_g^2\cdot \Delta t_g/2$. | ||
| − | + | ===Weitere Angaben zu den betrachteten Impulsantworten=== | |
| − | + | Alle Angaben sind ohne Berücksichtigung der Verzögerung $\tau_g$ | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | '''(1) Rechteckimpuls''' ⇒ ''Rectangular Impulse'' | |
| − | + | *Der Impuls $g(t)$ hat im Bereich $\pm \Delta t_g/2$ die konstante Höhe $A_g$ und ist außerhalb Null. | |
| − | + | *Die Spektralfunktion $G(f)=A_g\cdot \Delta t_g \cdot {\rm si}(\pi\cdot \Delta t_g \cdot f)$ besitzt Nullstellen in äquidistanten Abständen $1/\Delta t_g$. | |
| − | + | *Die Impulsenergie ist $E_g=A_g^2\cdot \Delta t_g$. | |
| − | |||
| − | |||
| − | |||
| − | |||
| + | '''(2) Gaußimpuls''' ⇒ ''Gaussian Imulse'' | ||
| + | *Der Impuls $g(t)=A_g\cdot {\rm e}^{-\pi\cdot(t/\Delta t_g)^2}$ ist unendlich weit ausgedehnt. Das Maximum ist $g(t= 0)=A_g$. | ||
| + | *Je kleiner die äquivalente Zeitdauer $\Delta t_g$ ist, um so breiter und niedriger ist das Spektrum $G(f)=A_g \cdot \Delta t_g \cdot {\rm e}^{-\pi\hspace{0.05cm}\cdot\hspace{0.05cm}(f\hspace{0.05cm}\cdot\hspace{0.05cm} \Delta t_g)^2}$. | ||
| + | *Die Impulsenergie ist $E_g=A_g^2\cdot \Delta t_g/\sqrt{2}$. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | '''(3) Exponentialimpuls''' ⇒ ''Exponential Impulse'' | |
| − | + | *Der Impuls ist für $t<0$ identisch Null und für positive Zeiten unendlich weit ausgedehnt ⇒ $g(t)=A_g\cdot {\rm e}^{-t/\Delta t_g}$. | |
| − | * | + | *$g(t)$ ist (stark) unsymmetrisch ⇒ das Spektrum $G(f)=A_g \cdot \Delta t_g/( 1 + {\rm j} \cdot 2\pi \cdot f \cdot \Delta t_g)$ ist komplexwertig; |
| + | *Die Impulsenergie ist $E_g=A_g^2\cdot \Delta t_g/2$. | ||
| − | |||
| − | + | ==Exercises== | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | *First, select the number $(1,\ 2, \text{...} \ )$ of the task to be processed. The number $0$ corresponds to a "Reset": Same setting as at program start. | |
| − | + | *A task description is displayed. The parameter values are adjusted. Solution after pressing "Show Solution". | |
| + | Both the input signal $x(t)$ and the impulse response $h(t)$ of the filter are are normalized, dimensionless and energy-limited ("time-limited pulses"). | ||
| + | :*Alle Zeiten, Frequenzen, Signalwerte und Leistungen sind normiert zu verstehen. | ||
| − | |||
| − | *die | + | '''Deutsch''' |
| − | + | *Wählen Sie zunächst die Nummer $(1,\ 2, \text{...})$ der zu bearbeitenden Aufgabe. Die Nummer $0$ entspricht einem "Reset": Gleiche Einstellung wie beim Programmstart. | |
| − | + | *Eine Aufgabenbeschreibung wird angezeigt. Die Parameterwerte sind angepasst. Lösung nach Drücken von "Musterlösung". | |
| − | + | *Sowohl das Eingangssignal $x(t)$ als auch die Impulsantwort $h(t)$ sind normiert, dimensionslos und energiebegrenzt (zeitlich begrenzte Impulse). | |
| − | + | :*Alle Zeiten, Frequenzen, Signalwerte und Leistungen sind normiert zu verstehen. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | * | ||
| + | {{BlaueBox|TEXT= | ||
| + | '''(1)''' Der Eingangsimpuls sei gaußförmig mit $A_g=1,\ \Delta t_g=1,\ \tau_g=1$. Welche Einstellung führt zum "Matched–Filter"? Wie groß ist $10 \cdot \lg \ \rho_{\rm MF}$ mit $N_0=0.01$? }} | ||
| − | === | + | :* Das Matched–Filter muss ebenfalls einen gaußförmigen Verlauf haben und es muss gelten: $\Delta t_h=\Delta t_g=1,\ \tau_h =\tau_g=1$ ⇒ $T_{\rm D} = \tau_h +\tau_g=2$. |
| + | :* Das (momentane) Signal–zu–Rauschleistungsverhältnis am Filterausgang ist $\rho _{\rm MF} = { {2 \cdot E_g } }/{ {N_0 } } \approx 141.4$ ⇒ $10 \cdot \lg \ \rho _{\rm MF} \approx 21.5$ dB. | ||
| + | :* Mit keinem anderen Filter als dem Matched–Filter ist dieses $\rm SNR$ (oder ein noch besseres) zu erreichen. | ||
| − | |||
| − | |||
| − | |||
| − | |||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | + | '''(2)''' Das Matched–Filter bei rechteckförmigen Eingangsimpuls mit $A_g=1,\ \Delta t_g=1,\ \tau_g=0$ ist ein Spalt–Tiefpass ⇒ rechteckförmige Impulsantwort. <br> Wie groß ist hier $10 \cdot \lg \ \rho_{\rm MF}$ mit $N_0=0.01$? Interpretieren Sie alle dargestellten Grafiken und die numerischen Ergebnisse auf verschiedene Art und Weise.}} | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | :* Die eingestellten Filterparameter sind $A_h=A_g=1, \ \Delta t_h=\Delta t_g=1,\ \tau_h =\tau_g=0$ ⇒ $T_{\rm D} = \tau_h +\tau_g=0$ ⇒ $\rho _{\rm MF} = 200$ ⇒ $10 \cdot \lg \ \rho _{\rm MF} \approx 23$ dB. | ||
| + | :* Die Impulsenergie ist das Integral über $g^2(t)$ ⇒ $E_g = A_g^2 \cdot \Delta t_g=1$ ⇒ $\rho _{\rm MF} = 2 \cdot E_g /N_0 =200$. $T_{\text{D, opt} }=0$ ist hier implizit berücksichtigt. | ||
| + | :* Eine andere Gleichung lautet: $\rho_d (T_{\rm D}) =d_{\rm S}^2 (T_{\rm D})/\sigma_d^2$. Die Rauschvarianz kann z. B. als Integral über $h^2(t)$ berechnet werden: $\sigma_d^2= N_0 \cdot \Delta t_h/2 = 0.005$. | ||
| + | :* Das Nutzsignal $d_{\rm S} (t)= g(t) * h(t)$ hat einen dreieckförmigen Verlauf mit dem Maximum $d_{\rm S} (T_{\rm D, \ opt} = 0 )= 1$ ⇒ $\rho_d (T_{\rm D, \ opt} = 0 ) = 200= \rho _{\rm MF}$. | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | '''( | + | '''(3)''' Es gelten weiter die Einstellungen von '''(2)''' mit Ausnahme von $N_0=0.02 $ statt $N_0=0.01$. Welche Veränderungen sind erkennbar? }} |
| − | + | :* Der einzige Unterschied ist die doppelt so große Rauschvarianz $\sigma_d^2= 0.01$ ⇒ $\rho_d (T_{\rm D, \ opt} = 0 ) = 100= \rho _{\rm MF}$ ⇒ $10 \cdot \lg \rho_{\rm MF} =20$ dB. | |
| − | :* | ||
| − | |||
| − | |||
| − | |||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | '''( | + | '''(4)''' Es gelten weiter die Einstellungen von '''(3)''' mit Ausnahme von $T_{\rm D} = 0.1 $ statt $T_{\rm D, \ opt} = 0$. Wie wirkt sich dieser nichtoptimale Detektionszeitpunkt aus? }} |
| + | :* Nun ist der Nutzabtastwert $d_{\rm S} (T_{\rm D} = 0.1 )= 0.9$ kleiner ⇒ $\rho_d (T_{\rm D} = 0.1 ) =0.9^2/0.01= 81< \rho _{\rm MF}$. Es ergibt sich eine Verschlechterung um knapp ein dB. | ||
| + | :* Für die weiteren Aufgaben wird vom optimalen Detektionszeitpunkt $T_{\rm D, \ opt}$ ausgegangen, wenn nicht explizit etwas anderes angegeben wird. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | '''( | + | '''(5)''' Es gelten wieder die Einstellungen von '''(3)''' mit Ausnahme einer niedrigeren Impulsantwort $A_h = 0.8 $ statt $A_h = 1$. Interpretieren Sie die Veränderungen. }} |
| − | + | :* Es handelt sich auch mit $A_h \ne A_g$ um ein Matched-Filter, solange $h(t)$ formgleich mit $g(t)$ ist ⇒ $\rho _{\rm MF} = { {2 \cdot E_g } }/{ {N_0 } } =100$ ⇒ $10 \cdot \lg \rho_{\rm MF} =20$ dB. | |
| − | :* | + | :* Die Gleichung $\rho_d (T_{\rm D}=0) =d_{\rm S}^2 (T_{\rm D}=0)/\sigma_d^2$ führt zum gleichen Ergebnis, da ${d_{\rm S}}^2 (T_{\rm D})$ und $\sigma_d^2$ gegenüber '''(3)''' jeweils um den Faktor $0.8^2$ vermindert wird. |
| − | |||
| − | |||
| − | |||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | '''( | + | '''(6)''' Gegenüber '''(5)''' wird nun die Höhe des Eingangsimpulses $g(t)$ von $A_g = 1$ auf $A_g = 1.25$ erhöht. Beschreibt hier $h(t)$ ein Matched-Filter? Wie groß ist $\rho_{\rm MF}$? }} |
| − | + | :* Auch hier liegt ein Matched-Filter vor, da $h(t)$ und $g(t)$ formgleich sind. Mit $E_g = 1.25^2$: $\rho _{\rm MF} = { {2 \cdot 1.25^2 } }/{ 0.02 } =156.25$ ⇒ $10 \cdot \lg \rho_{\rm MF} \approx 21.9$ dB. | |
| − | + | :* Der höhere Wert $21.9$ dB gegenüber '''(5)''' lässt sich dadurch erklären, dass bei gleicher Rauschvarianz $\sigma_d^2= 0.0064$ der Nutzabtastwert wieder ${d_{\rm S}} (T_{\rm D}) = 1$ ist. | |
| − | |||
| − | :* | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | '''( | + | '''(7)''' Wir gehen weiter von der Rechteck–Rechteck–Kombination aus mit $A_h=A_g=1,\ \Delta t_h=\Delta t_g=1,\ \tau_h=\tau_g=0,\ N_0 =0.02,\ T_{\rm D}=0$. <br> Interpretieren Sie die Ergebnisse nach Variation der äquivalenten Impulsdauer $\Delta t_h$ von $h(t)$ im Bereich $0.6$ ... $1.4$. Nutzen Sie die Grafikdarstellung über $\Delta t_h$. }} |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | :* Das Optimum ergibt sich erwartungsgemäß für die äquivalente Impulsdauer $\Delta t_h=\Delta t_g=1$. Dann ist $10 \cdot \lg \ \rho_d (T_{\rm D, \ opt} = 0 ) =20$ dB $\big(= 10 \cdot \lg \rho_{\rm MF}\big)$. | |
| − | + | :* Ist $\Delta t_h<\Delta t_g=1$, so ist das Nutzsignal trapezförmig. Für $\Delta t_h=0.6$: $d_{\rm S} (T_{\rm D}=0)= 0.6$ und $\sigma_d^2\approx0.006$ ⇒ $10 \cdot \lg \ \rho_d (T_{\rm D, \ opt} = 0 ) \approx 17.8$ dB. | |
| − | :* | + | :* Auch für $\Delta t_h>1$ ist das Nutzsignal trapezförmig, aber trotzdem $d_{\rm S} (T_{\rm D}=0)= 1$. Die Rauschvarianz $\sigma_d^2$ nimmt kontinuierlich mit $\Delta t_h$ zu. |
| − | + | :* Für $\Delta t_h=1.4$ ist $\sigma_d^2=0.0140$ ⇒ $10 \cdot \lg \ \rho_d (T_{\rm D, \ opt} = 0 ) \approx 18.5$ dB. Gegenüber dem Matched–Filter $(\Delta t_h=1)$ beträgt die Verschlechterung ca. $1.5$ dB. | |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | '''( | + | '''(8)''' Interpretieren Sie nun die Ergebnisse für verschiedene $\Delta t_g$ des Eingangsimpulses $g(t)$ im Bereich $0.6$ ... $1.4$. Nutzen Sie die Grafikdarstellung über $\Delta t_g$. }} |
| − | :* | + | :* Beachten Sie: Die blaue Kurve $10 \cdot \lg \ \rho_d (T_{\rm D,\ opt} )$ ist die Differenz aus $20\cdot \lg \ \big [{K \cdot d_{\rm S}} (T_{\rm D,\ opt}) \big ]$ (violette Kurve) und $20\cdot \lg \ \big [K \cdot \sigma_d \big ]$ (grüne Kurve). |
| − | :* | + | :* Beim betrachteten Parametersatz und $K=10$ ist der grüne Term $20\cdot \lg \ \big [K \cdot \sigma_d \big ] = 0$ dB für alle $\Delta t_g$ ⇒ die blaue und die violette Kurve sind identisch. |
| − | :* | + | :* Die blaue Kurve $10 \cdot \lg \ \rho_d (T_{\rm D,\ opt} )$ steigt von $15.6$ dB $($für $\Delta t_g = 0.6)$ bis $20$ dB $($für $\Delta t_g = 1)$ kontinuierlich an und bleibt für $\Delta t_g > 1$ dann konstant. |
| + | :* Die Einstellung $\Delta t_g = 1.4,\ \Delta t_h = 1$ ergibt aber kein Matched-Filter. Vielmehr gilt mit $\Delta t_h = \Delta t_g = 1.4$: $10 \cdot \lg \ \rho_{\rm MF}=10 \cdot \lg \ (2 \cdot E_g/N_0) \approx 21.5$ dB. | ||
| + | :* Die Grafikdarstellung über $\Delta t_h$ mit der Grundeinstellung $\Delta t_g = 1.4,\ \Delta t_h = 1$ zeigt nun einen monotonen Anstieg der blauen Kurve $10 \cdot \lg \ \rho_d (T_{\rm D,\ opt} )$. | ||
| + | :* Für $\Delta t_h = 0.6$ ergibt sich $10 \cdot \lg \ \rho_d (T_{\rm D,\ opt} )\approx 17.8$ dB, für $\Delta t_h = 1.4$ dagegen $10 \cdot \lg \ \rho_d (T_{\rm D,\ opt} )\approx 21.5$ dB $=10 \cdot \lg \ \rho_{\rm MF}$. | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | '''( | + | '''(9)''' Wir betrachten den Exponentialimpuls $g(t)$ und den Tiefpass erster Ordnung sowie $A_h=A_g=1,\ \Delta t_h=\Delta t_g=1,\ \tau_h=\tau_g=0,\ N_0 =0.02,\ T_{\rm D}=1$. <br> Erfüllt diese Einstellung den Matched-Filter-Kriterien? Begründen Sie Ihre Antworten mit möglichst vielen Argumenten. }} |
| − | :* Das | + | :* Hier gilt $h(t)=g(t)$. Bei einer Matched-Filter-Konfiguration müsste $h(t)={\rm const.} \cdot g(T_{\rm D}-t)$ gelten. |
| − | + | :* Das Detektionsnutzsignal $d_{\rm S}(t)$ hat keinen symmetrischen Verlauf um das Maximum. Beim Matched-Filter müsste $d_{\rm S}(T_{\rm D}-t) = d_{\rm S}(T_{\rm D}+t) $ gelten. | |
| + | :* Trotz $\Delta t_h=\Delta t_g$ ist $10 \cdot \lg \ \rho_d (T_{\rm D,\ opt}) \approx 14.3$ dB kleiner als $10 \cdot \lg \ \rho _{\rm MF} = 10 \cdot \lg \ 2 \cdot E_g/N_0 \approx 17$ dB. | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | '''( | + | '''(10)''' Was ändert sich bei sonst gleichen Einstellungen mit dem "extrem akausalen Filter"? Erfüllt die Einstellung die Matched-Filter-Kriterien? Begründung. }} |
| − | + | :* Hier gilt nun $h(t)=g(-t)$ und das Detektionsnutzsignal $d_{\rm S}(t)$ ist symmetrisch um $t=0$. Sinnvollerweise sollte hier $T_{\rm D} = 0 $ gewählt werden. | |
| − | :* | + | :* Damit erhält man für $10 \cdot \lg \ \rho_d (T_{\rm D,\ opt}) =10 \cdot \lg \ d_{\rm S}^2 (T_{\rm D,\ opt})/\sigma_d^2 = 17$ dB den gleichen Wert wie für $10 \cdot \lg \ \rho _{\rm MF} = 10 \cdot \lg \ 2 \cdot E_g/N_0 = 17$ dB. |
| − | :* | + | :* Das Nutzsignal $d_{\rm S}(t)$ ist formgleich mit der Energie–AKF des Sendeimulses $g(t)$. Das Matched-Filter bündelt die Energie um den geeigneten Zeitpunkt $T_{\rm D,\ opt}$. |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | '''( | + | '''(11)''' Mit welchem Rechteckimpuls $g(t)$ erreicht man mit dem entsprechend angepassten Filter das gleiche $\rho _{\rm MF}=50$ wie in Aufgabe '''(10)'''? <br> Mit $A_h=A_g=1,\ \Delta t_h=\Delta t_g=0.5$ oder mit $A_h=A_g=0.5,\ \Delta t_h=\Delta t_g=1$ ? }} |
| − | + | :* Aus der Gleichung $\rho _{\rm MF} = 2 \cdot E_g/N_0$ geht bereits hervor, dass das SNR nur von der Energie $E_g$ des Eingangsimpulses abhängt und nicht von dessen Form. | |
| − | :* | + | :* Der Exponentialimpuls mit $A_g=1,\ \Delta t_g=1$ hat die Energie $E_g=0.5$. Der Rechteckimpuls mit $A_g=1,\ \Delta t_g=0.5$ ebenfalls ⇒ $\rho _{\rm MF}=50$. |
| − | + | :* Dagegen besitzt der Rechteckimpuls mit $A_g=0.5,\ \Delta t_g=1$ eine kleinere Energie ⇒ $E_g=0.25$ ⇒ $\rho _{\rm MF}=25$ ⇒ $10 \cdot \lg \ \rho _{\rm MF} = 14$ dB. | |
| − | :* | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | == | + | ==Applet Manual== |
<br> | <br> | ||
[[File:Anleitung_abtast.png|right|600px]] | [[File:Anleitung_abtast.png|right|600px]] | ||
| Line 318: | Line 286: | ||
'''(K)''' Bereich für Übungen: Aufgabenauswahl, Fragen, Musterlösung | '''(K)''' Bereich für Übungen: Aufgabenauswahl, Fragen, Musterlösung | ||
<br clear=all> | <br clear=all> | ||
| − | == | + | ==About the Authors== |
Dieses interaktive Berechnungstool wurde am [http://www.lnt.ei.tum.de/startseite Lehrstuhl für Nachrichtentechnik] der [https://www.tum.de/ Technischen Universität München] konzipiert und realisiert. | Dieses interaktive Berechnungstool wurde am [http://www.lnt.ei.tum.de/startseite Lehrstuhl für Nachrichtentechnik] der [https://www.tum.de/ Technischen Universität München] konzipiert und realisiert. | ||
| − | *Die erste Version wurde | + | *Die erste Version wurde 2006 von [[Biographies_and_Bibliographies/An_LNTwww_beteiligte_Studierende#Markus_Elsberger_.28Diplomarbeit_LB_2006.29|Markus Elsberger]] im Rahmen seiner Diplomarbeit (LB) mit "FlashMX–Actionscript" erstellt (Betreuer: [[Biographies_and_Bibliographies/An_LNTwww_beteiligte_Mitarbeiter_und_Dozenten#Prof._Dr.-Ing._habil._G.C3.BCnter_S.C3.B6der_.28am_LNT_seit_1974.29|Günter Söder]]). |
| − | * 2020 wurde das Programm von [[ | + | * 2020 wurde das Programm von [[Biographies_and_Bibliographies/An_LNTwww_beteiligte_Studierende#Carolin_Mirschina_.28Ingenieurspraxis_Math_2019.2C_danach_Werkstudentin.29|Carolin Mirschina]] im Rahmen einer Werkstudententätigkeit auf "HTML5" umgesetzt und neu gestaltet (Betreuer: [[Biographies_and_Bibliographies/Beteiligte_der_Professur_Leitungsgebundene_%C3%9Cbertragungstechnik#Tasn.C3.A1d_Kernetzky.2C_M.Sc._.28bei_L.C3.9CT_seit_2014.29|Tasnád Kernetzky]]). |
| Line 330: | Line 298: | ||
| − | == | + | ==Once again: Open Applet in new Tab== |
| − | {{LntAppletLink| | + | {{LntAppletLink|sampling}} |
Latest revision as of 16:48, 28 May 2021
Contents
Applet Description
Das Applet soll die Eigenschaften des so genannten "Matched-Filters" $({\rm MF})$ verdeutlichen. Dieses dient zur optimalen Bestimmung des Vorhandenseins (Detektion) der Amplitude und/oder der Lage einer bekannten Signalform in einer stark verrauschten Umgebung. Oder allgemeiner gesprochen: Das Matched-Filter – manchmal auch als "Optimalfilter" oder als "Korrelationsfilter" bezeichnet – dient dem Nachweis der Signalexistenz.
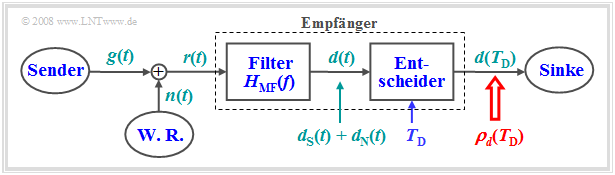
Die Grafik zeigt den so genannten Matched-Filter-Empfänger:
- Dieser kann mit größtmöglicher Sicherheit – anders ausgedrückt: mit maximalem Signal–zu–Rausch–Verhältnis $($englisch: signal–to–noise–ratio, $\rm SNR)$ – entscheiden, ob ein durch additives Rauschen $n(t)$ gestörtes impulsförmiges Nutzsignal $g(t)$ vorhanden ist oder nicht.
- Eine Anwendung ist die Radartechnik, bei der man zwar die Impulsform $g(t)$ kennt, nicht aber, wann der Impuls gesendet wurde und mit welcher Stärke und Verzögerung dieser ankommt.
- Das Matched-Filter wird aber auch als Empfangsfilter in digitalen Übertragungssystemen (oder zumindest als Teil davon) eingesetzt, um die Fehlerwahrscheinlichkeit des Systems zu minimieren.
Alle Parameter, Zeiten und Frequenzen sind als normierte Größen zu verstehen und damit dimensionslos.
- Für den Eingangsimpuls $g(t)$ sind "Rechteck", "Gauß" und "Exponential" einstellbar, die jeweils durch die Impulsamplitude $A_g$, die äquivalente Impulsdauer $\Delta t_g$ sowie die Verschiebung $\tau_g$ gegenüber dem (hinsichtlich Zeit) symmetrischen Fall beschrieben werden. Weitere Informationen im Abschnitt Weitere Angaben zu den betrachteten Eingangsimpulsen.
- Für das Empfangsfilter kann zwischen den Alternativen "Spalt–Tiefpass", "Gauß–Tiefpass", "Tiefpass erster Ordnung"und "Tiefpass 4" gewählt werden. Dargestellt werden die jeweiligen Impulsantworten $h(t)$, gekennzeichnet durch deren Höhe $A_h$, die äquivalente Dauer $\Delta t_h$ und die Verschiebung $\tau_h$. Weitere Informationen im Abschnitt Weitere Angaben zu den betrachteten Impulsantworten.
- Weitere Eingabeparameter sind der Detektionszeitpunkt $T_{\rm D}$ sowie die ebenfalls normierte Rauschleistungsdichte $N_0$ am Empfängereingang.
Als Numerikwerte ausgegeben werden
- die Energie $E_g$ des Eingangsimpulses $g(t)$, der Nutzabtastwert $d_{\rm S} (T_{\rm D})$ am Filterausgang sowie die Rauschvarianz $\sigma_d^2$ am Filterausgang,
- das Signal–zu–Rausch–Verhältnis $\rm (SNR)$ $\rho_{d} (T_{\rm D})$ am Filterausgang und die zugehörige dB–Angabe $10 \cdot \lg \ \rho_{d} (T_{\rm D})$,
- der hierfür maximale Wert $10 \cdot \lg \ \rho_{\rm MF}$.
Erfüllt die eingegebene Konfiguration die Matched-Filter-Bedingungen, dann gilt: $10 \cdot \lg \ \rho_{d} (T_{\rm D,\ opt}) = 10 \cdot \lg \ \rho_{\rm MF}$.
Theoretical Background
Detailbeschreibung des zugrunde liegenden Modells
Für die einzelnen Komponenten des obigen Blockschaltbild gelten folgende Voraussetzungen:
- Der Nutzanteil $g(t)$ des Empfangssignals $r(t)=g(t)+n(t)$ sei impulsförmig und somit energiebegrenzt. Das heißt: Das Integral über $ [g(t) ]^2$ von $–∞$ bis $+∞$ liefert den endlichen Wert $E_g$.
- Das Störsignal $n(t)$ sei Weißes Gaußsches Rauschen mit der Rauschleistungsdichte $N_0$.
- Das Filterausgangssignal $d(t)= d_{\rm S}(t) + d_{\rm N}(t)$ besteht additiv aus zwei Anteilen. Der Anteil $d_{\rm S}(t)$ geht auf das $\rm S\hspace{0.04cm}$ignal $g(t)$ zurück, $d_{\rm N}(t)$ auf das $\rm N\hspace{0.04cm}$oise $n(t)$.
- Der Empfänger, bestehend aus einem linearen Filter ⇒ Frequenzgang $H_{\rm MF}(f)$ und dem Entscheider, ist so zu dimensionieren, dass das momentane S/N-Verhältnis am Ausgang maximal wird:
- $$\rho _d ( {T_{\rm D} } ) = \frac{ {d_{\rm S} ^2 ( {T_{\rm D} } )} }{ {\sigma_d^2 } }\mathop = \limits^{\rm{!} }\hspace{0.1cm} {\rm{Maximum} }.$$
- Hierbei bezeichnen ${σ_d}^2$ die Varianz (Leistung) von $d_{\rm N}(t)$ und $T_{\rm D}$ den (geeignet gewählten) Detektionszeitpunkt.
Matched-Filter-Optimierung
Gegeben sei ein energiebegrenztes Nutzsignal $g(t)$ mit dem zugehörigen Spektrum $G(f)$. Damit kann das Filterausgangssignal zum Detektionszeitpunkt $T_{\rm D}$ für jedes beliebige Filter mit Impulsantwort $h(t)$ und Frequenzgang $H(f) =\mathcal{ F}\{h(t)\}$ geschrieben werden (ohne Berücksichtigung des Rauschens ⇒ Index $\rm S$ für „Signal”):
- $$d_{\rm S} ( {T_{\rm D} } ) = g(t) * h(t) = \int_{ - \infty }^{ + \infty } {G(f) \cdot H(f) \cdot {\rm{e}}^{ {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f \hspace{0.05cm}\cdot \hspace{0.05cm}T_{\rm D} }\hspace{0.1cm} {\rm{d}}f} .$$
Der „Rauschanteil” $d_{\rm N}(t)$ des Filterausgangssignals (Index $\rm N$ für „Noise”) rührt allein vom Weißen Rauschen $n(t)$ am Eingang des Empfängers her. Für seine Varianz (Leistung) gilt unabhängig vom Detektionszeitpunkt $T_{\rm D}$:
- $$\sigma _d ^2 = \frac{ {N_0 } }{2} \cdot \int_{ - \infty }^{ + \infty } {\left| {H(f)} \right|^{\rm{2} }\hspace{0.1cm} {\rm{d} }f} .$$
Damit lautet das hier vorliegende Optimierungsproblem:
- $$\rho _d ( {T_{\rm D} } ) = \frac{ {\left| {\int_{ - \infty }^{ + \infty } {G(f) \cdot H(f) \cdot {\rm{e} }^{ {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f \hspace{0.05cm}\cdot \hspace{0.05cm}T_{\rm D} }\hspace{0.1cm} {\rm{d} }f} } \right|^2 } }{ {N_0 /2 \cdot \int_{ - \infty }^{ + \infty } {\left| {H(f)} \right|^{\rm{2} }\hspace{0.1cm} {\rm{d} }f} } } \stackrel{!}{=} {\rm{Maximum} }.$$
Dieser Quotient wird für den folgenden Frequenzgang $H(f)$ am größten wird:
- $$H(f) = H_{\rm MF} (f) = K_{\rm MF} \cdot G^{\star} (f) \cdot {\rm e}^{- {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f \hspace{0.05cm}\cdot \hspace{0.05cm}T_{\rm D} } . $$
- Damit erhält man für das Signal–zu–Rauschleistungsverhältnis am Matched–Filter–Ausgang $($unabhängig von der dimensionsbehafteten Konstante $K_{\rm MF})$:
- $$\rho _d ( {T_{\rm D} } ) = { {2 \cdot E_g } }/{ {N_0 } } \hspace{0.5cm}\Rightarrow \hspace{0.5cm} \rho _{\rm MF}.$$
- $E_g$ bezeichnet die Energie des Eingangsimpulses, die man nach dem Satz von Parseval sowohl im Zeit– als auch im Frequenzbereich berechnen kann:
- $$E_g = \int_{ - \infty }^{ + \infty } {g^2 (t)\hspace{0.1cm}{\rm{d} }t} = \int_{ - \infty }^{ + \infty } {\left \vert {G(f)} \right\vert ^{\rm{2} }\hspace{0.1cm} {\rm d}f} .$$
$\text{Herleitung des Matched–Filter–Kriteriums:}$
$(1)$ Die Schwarzsche Ungleichung lautet mit den beiden (im allgemeinen komplexen) Funktionen $A(f)$ und $B(f)$:
- $$\left \vert {\int_a^b {A(f) \cdot B(f)\hspace{0.1cm}{\rm{d} }f} } \right \vert ^2 \le \int_a^b {\left \vert {A(f)} \right \vert^{\rm{2} } \hspace{0.1cm}{\rm{d} }f} \cdot \int_a^b {\left\vert {B(f)} \right \vert^{\rm{2} } \hspace{0.1cm}{\rm{d} }f} .$$
$(2)$ Wir wenden nun diese Gleichung auf das Signal–zu–Rauschverhältnis an:
- $$\rho _d ( {T_{\rm D} } ) = \frac{ {\left \vert {\int_{ - \infty }^{ + \infty } {G(f) \cdot H(f) \cdot {\rm{e} }^{ {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f \hspace{0.05cm}\cdot \hspace{0.05cm}T_{\rm D} } \hspace{0.1cm}{\rm{d} }f} } \right \vert^2 } }{ {N_0 /2 \cdot \int_{ - \infty }^{ + \infty } {\left \vert {H(f)} \right \vert^{\rm{2} }\hspace{0.1cm} {\rm{d} }f} } }.$$
$(3)$ Mit $A(f) = G(f)$ und $B(f) = H(f) · {\rm e}^{ {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f \hspace{0.05cm}\cdot \hspace{0.05cm}T_{\rm D} }$ ergibt sich somit die folgende Schranke:
- $$\rho_d ( {T_{\rm D} } ) \le \frac{1}{ {N_0 /2} } \cdot \int_{ - \infty }^{ + \infty } {\left \vert {G(f)} \right \vert^{\rm{2} } }\hspace{0.1cm}{\rm{d} }f .$$
$(4)$ Wir setzen für den Filterfrequenzgang nun versuchsweise ein:
- $$H(f) = H_{\rm MF} (f) = K_{\rm MF} \cdot G^{\star} (f) \cdot {\rm{e} }^{- {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f \hspace{0.05cm}\cdot \hspace{0.05cm}T_{\rm D} }.$$
$(5)$ Dann erhält man aus der obigen Gleichung $(2)$ folgendes Ergebnis:
- $$\rho _d ( {T_{\rm D} } ) = \frac{ {\left \vert K_{\rm MF}\cdot {\int_{ - \infty }^{ + \infty } {\left \vert {G(f)} \right \vert ^{\rm{2} }\hspace{0.1cm} {\rm{d} }f} } \right \vert ^2 } }{ {N_0 /2 \cdot K_{\rm MF} ^2 \cdot \int_{ - \infty }^{ + \infty } {\left \vert {G(f)} \right \vert ^{\rm{2} }\hspace{0.1cm} {\rm{d} }f} } } = \frac{1}{ {N_0 /2} } \cdot \int_{ - \infty }^{ + \infty } {\left \vert {G(f)} \right \vert ^{\rm{2} }\hspace{0.1cm} {\rm{d} }f} .$$
$\text{Das heißt:}$
- Mit dem Ansatz $(4)$ für das Matched–Filter $H_{\rm MF}(f)$ wird in obiger Abschätzung tatsächlich der maximal mögliche Wert erreicht.
- Mit keinem anderen Filter $H(f) ≠ H_{\rm MF}(f)$ kann man ein höheres Signal–zu–Rauschleistungsverhältnis erzielen.
- Das Matched–Filter ist in Bezug auf das ihm zugrunde gelegte Maximierungskriterium optimal.
$\text{Beispiel 1:}$ Ein rechteckförmiger Impuls $g(t)$ mit Amplitude $\rm 1\hspace{0.05cm}V$, Dauer $0.5\hspace{0.05cm} \rm ms$ und unbekannter Lage soll in einer verrauschten Umgebung aufgefunden werden.
- Somit ist die Impulsenergie $E_g = \rm 5 · 10^{–4} \hspace{0.05cm}V^2s$.
- Die Rauschleistungsdichte sei $N_0 = \rm 10^{–6} \hspace{0.05cm}V^2/Hz$.
Das beste Ergebnis ⇒ das maximale S/N–Verhältnis erzielt man mit dem Matched-Filter:
- $$\rho _d ( {T_{\rm D} } ) = \frac{ {2 \cdot E_g } }{ {N_0 } } = \frac{ {2 \cdot 5 \cdot 10^{-4}\, {\rm V^2\,s} } }{ {10^{-6}\, {\rm V^2/Hz} } } = 1000 \hspace{0.3cm}\Rightarrow\hspace{0.3cm} 10 \cdot {\rm lg}\hspace{0.15cm}\rho _d ( {T_{\rm D} } ) = 30\,{\rm dB}= 10 \cdot {\rm lg}\hspace{0.15cm}\rho_{\rm MF}.$$
Interpretation des Matched-Filters
Auf der letzten Seite wurde der Frequenzgang des Matched-Filters wie folgt hergeleitet:
- $$H_{\rm MF} (f) = K_{\rm MF} \cdot G^{\star} (f) \cdot {\rm{e} }^{- {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f \hspace{0.05cm}\cdot \hspace{0.05cm}T_{\rm D} } .$$
Durch Fourierrücktransformation erhält man die dazugehörige Impulsantwort:
- $$h_{\rm MF} (t) = K_{\rm MF} \cdot g(T_{\rm D} - t).$$
Diese beiden Funktionen lassen sich wie folgt interpretieren:
- Das Matched-Filter ist durch den Term $G^{\star}(f)$ an das Spektrum des aufzufindenden Impulses $g(t)$ angepasst – daher sein Name (englisch: to match ≡ anpassen).
- Die Konstante $K_{\rm MF}$ ist aus Dimensionsgründen notwendig.
- Ist $g(t)$ ein Spannungsimpuls, so hat diese Konstante die Einheit „Hz/V”. Der Frequenzgang ist somit dimensionslos.
- Die Impulsantwort $h_{\rm MF}(t)$ ergibt sich aus dem Nutzsignal $g(t)$ durch Spiegelung ⇒ aus $g(t)$ wird $g(–t)$ sowie einer Verschiebung um $T_{\rm D}$ nach rechts.
- Der früheste Detektionszeitpunkt $T_{\rm D}$ folgt für realisierbare Systeme aus der Bedingung $h_{\rm MF}(t < 0)\equiv 0$ $($„Kausalität”, siehe Buch Lineare zeitinvariante Systeme$)$.
- Der Nutzanteil $d_{\rm S} (t)$ des Filterausgangssignals ist formgleich mit der Energie-AKF $\varphi^{^{\bullet} }_{g} (t )$ und gegenüber dieser um $T_{\rm D}$ verschoben. Es gilt:
- $$d_{\rm S} (t) = g(t) * h_{\rm MF} (t) = K_{\rm MF} \cdot g(t) * g(T_{\rm D} - t) = K_{\rm MF} \cdot \varphi^{^{\bullet} }_{g} (t - T_{\rm D} ).$$
$\text{Bitte beachten Sie:}$ Bei einem energiebegrenzten Signal $g(t)$ kann man nur die Energie–AKF angeben:
- $$\varphi^{^{\bullet} }_g (\tau ) = \int_{ - \infty }^{ + \infty } {g(t) \cdot g(t + \tau )\,{\rm{d} }t} .$$
Gegenüber der AKF-Definition eines leistungsbegrenzten Signals $x(t)$, nämlich
- $$\varphi _x (\tau ) = \mathop {\lim }_{T_{\rm M} \to \infty } \frac{1}{ {T_{\rm M} } }\int_{ - T_{\rm M} /2}^{+T_{\rm M} /2} {x(t) \cdot x(t + \tau )\hspace{0.1cm}\,{\rm{d} }t} ,$$
wird bei der Berechnung der Energie-AKF auf die Division durch die Messdauer $T_{\rm M}$ sowie auf den Grenzübergang $T_{\rm M} → ∞$ verzichtet.
$\text{Beispiel 2:}$ Wir gehen davon aus, dass der Rechteckimpuls zwischen $\rm 2\hspace{0.08cm}ms$ und $\rm 2.5\hspace{0.08cm}ms$ liegt und der Detektionszeitpunkt $T_{\rm D} =\rm 2\hspace{0.08cm}ms$ gewünscht wird.
Unter diesen Voraussetzungen gilt:
- Die Matched–Filter–Impulsantwort $h_{\rm MF}(t)$ muss im Bereich von $t_1 (= 4 - 2.5) =\rm 1.5\hspace{0.08cm}ms$ bis $t_2 (= 4 - 2) =\rm 2\hspace{0.08cm}ms$ konstant sein.
- Für $t < t_1$ sowie für $t > t_2$ darf sie keine Anteile besitzen.
- Der Betragsfrequenzgang $\vert H_{\rm MF}(f)\vert$ ist hier $\rm si$–förmig.
- Die Höhe der Impulsantwort $h_{\rm MF}(t)$ spielt für das S/N–Verhältnis keine Rolle, da dieses unabhängig von $K_{\rm MF}$ ist.
Weitere Angaben zu den betrachteten Eingangsimpulsen
Alle Angaben sind ohne Berücksichtigung der Verzögerung $\tau_g$
(1) Rechteckimpuls ⇒ Rectangular Impulse
- Der Impuls $g(t)$ hat im Bereich $\pm \Delta t_g/2$ die konstante Höhe $A_g$ und ist außerhalb Null.
- Die Spektralfunktion $G(f)=A_g\cdot \Delta t_g \cdot {\rm si}(\pi\cdot \Delta t_g \cdot f)$ besitzt Nullstellen in äquidistanten Abständen $1/\Delta t_g$.
- Die Impulsenergie ist $E_g=A_g^2\cdot \Delta t_g$.
(2) Gaußimpuls ⇒ Gaussian Imulse
- Der Impuls $g(t)=A_g\cdot {\rm e}^{-\pi\cdot(t/\Delta t_g)^2}$ ist unendlich weit ausgedehnt. Das Maximum ist $g(t= 0)=A_g$.
- Je kleiner die äquivalente Zeitdauer $\Delta t_g$ ist, um so breiter und niedriger ist das Spektrum $G(f)=A_g \cdot \Delta t_g \cdot {\rm e}^{-\pi\hspace{0.05cm}\cdot\hspace{0.05cm}(f\hspace{0.05cm}\cdot\hspace{0.05cm} \Delta t_g)^2}$.
- Die Impulsenergie ist $E_g=A_g^2\cdot \Delta t_g/\sqrt{2}$.
(3) Exponentialimpuls ⇒ Exponential Impulse
- Der Impuls ist für $t<0$ identisch Null und für positive Zeiten unendlich weit ausgedehnt ⇒ $g(t)=A_g\cdot {\rm e}^{-t/\Delta t_g}$.
- $g(t)$ ist (stark) unsymmetrisch ⇒ das Spektrum $G(f)=A_g \cdot \Delta t_g/( 1 + {\rm j} \cdot 2\pi \cdot f \cdot \Delta t_g)$ ist komplexwertig;
- Die Impulsenergie ist $E_g=A_g^2\cdot \Delta t_g/2$.
Weitere Angaben zu den betrachteten Impulsantworten
Alle Angaben sind ohne Berücksichtigung der Verzögerung $\tau_g$
(1) Rechteckimpuls ⇒ Rectangular Impulse
- Der Impuls $g(t)$ hat im Bereich $\pm \Delta t_g/2$ die konstante Höhe $A_g$ und ist außerhalb Null.
- Die Spektralfunktion $G(f)=A_g\cdot \Delta t_g \cdot {\rm si}(\pi\cdot \Delta t_g \cdot f)$ besitzt Nullstellen in äquidistanten Abständen $1/\Delta t_g$.
- Die Impulsenergie ist $E_g=A_g^2\cdot \Delta t_g$.
(2) Gaußimpuls ⇒ Gaussian Imulse
- Der Impuls $g(t)=A_g\cdot {\rm e}^{-\pi\cdot(t/\Delta t_g)^2}$ ist unendlich weit ausgedehnt. Das Maximum ist $g(t= 0)=A_g$.
- Je kleiner die äquivalente Zeitdauer $\Delta t_g$ ist, um so breiter und niedriger ist das Spektrum $G(f)=A_g \cdot \Delta t_g \cdot {\rm e}^{-\pi\hspace{0.05cm}\cdot\hspace{0.05cm}(f\hspace{0.05cm}\cdot\hspace{0.05cm} \Delta t_g)^2}$.
- Die Impulsenergie ist $E_g=A_g^2\cdot \Delta t_g/\sqrt{2}$.
(3) Exponentialimpuls ⇒ Exponential Impulse
- Der Impuls ist für $t<0$ identisch Null und für positive Zeiten unendlich weit ausgedehnt ⇒ $g(t)=A_g\cdot {\rm e}^{-t/\Delta t_g}$.
- $g(t)$ ist (stark) unsymmetrisch ⇒ das Spektrum $G(f)=A_g \cdot \Delta t_g/( 1 + {\rm j} \cdot 2\pi \cdot f \cdot \Delta t_g)$ ist komplexwertig;
- Die Impulsenergie ist $E_g=A_g^2\cdot \Delta t_g/2$.
Exercises
- First, select the number $(1,\ 2, \text{...} \ )$ of the task to be processed. The number $0$ corresponds to a "Reset": Same setting as at program start.
- A task description is displayed. The parameter values are adjusted. Solution after pressing "Show Solution".
Both the input signal $x(t)$ and the impulse response $h(t)$ of the filter are are normalized, dimensionless and energy-limited ("time-limited pulses").
- Alle Zeiten, Frequenzen, Signalwerte und Leistungen sind normiert zu verstehen.
Deutsch
- Wählen Sie zunächst die Nummer $(1,\ 2, \text{...})$ der zu bearbeitenden Aufgabe. Die Nummer $0$ entspricht einem "Reset": Gleiche Einstellung wie beim Programmstart.
- Eine Aufgabenbeschreibung wird angezeigt. Die Parameterwerte sind angepasst. Lösung nach Drücken von "Musterlösung".
- Sowohl das Eingangssignal $x(t)$ als auch die Impulsantwort $h(t)$ sind normiert, dimensionslos und energiebegrenzt (zeitlich begrenzte Impulse).
- Alle Zeiten, Frequenzen, Signalwerte und Leistungen sind normiert zu verstehen.
(1) Der Eingangsimpuls sei gaußförmig mit $A_g=1,\ \Delta t_g=1,\ \tau_g=1$. Welche Einstellung führt zum "Matched–Filter"? Wie groß ist $10 \cdot \lg \ \rho_{\rm MF}$ mit $N_0=0.01$?
- Das Matched–Filter muss ebenfalls einen gaußförmigen Verlauf haben und es muss gelten: $\Delta t_h=\Delta t_g=1,\ \tau_h =\tau_g=1$ ⇒ $T_{\rm D} = \tau_h +\tau_g=2$.
- Das (momentane) Signal–zu–Rauschleistungsverhältnis am Filterausgang ist $\rho _{\rm MF} = { {2 \cdot E_g } }/{ {N_0 } } \approx 141.4$ ⇒ $10 \cdot \lg \ \rho _{\rm MF} \approx 21.5$ dB.
- Mit keinem anderen Filter als dem Matched–Filter ist dieses $\rm SNR$ (oder ein noch besseres) zu erreichen.
(2) Das Matched–Filter bei rechteckförmigen Eingangsimpuls mit $A_g=1,\ \Delta t_g=1,\ \tau_g=0$ ist ein Spalt–Tiefpass ⇒ rechteckförmige Impulsantwort.
Wie groß ist hier $10 \cdot \lg \ \rho_{\rm MF}$ mit $N_0=0.01$? Interpretieren Sie alle dargestellten Grafiken und die numerischen Ergebnisse auf verschiedene Art und Weise.
- Die eingestellten Filterparameter sind $A_h=A_g=1, \ \Delta t_h=\Delta t_g=1,\ \tau_h =\tau_g=0$ ⇒ $T_{\rm D} = \tau_h +\tau_g=0$ ⇒ $\rho _{\rm MF} = 200$ ⇒ $10 \cdot \lg \ \rho _{\rm MF} \approx 23$ dB.
- Die Impulsenergie ist das Integral über $g^2(t)$ ⇒ $E_g = A_g^2 \cdot \Delta t_g=1$ ⇒ $\rho _{\rm MF} = 2 \cdot E_g /N_0 =200$. $T_{\text{D, opt} }=0$ ist hier implizit berücksichtigt.
- Eine andere Gleichung lautet: $\rho_d (T_{\rm D}) =d_{\rm S}^2 (T_{\rm D})/\sigma_d^2$. Die Rauschvarianz kann z. B. als Integral über $h^2(t)$ berechnet werden: $\sigma_d^2= N_0 \cdot \Delta t_h/2 = 0.005$.
- Das Nutzsignal $d_{\rm S} (t)= g(t) * h(t)$ hat einen dreieckförmigen Verlauf mit dem Maximum $d_{\rm S} (T_{\rm D, \ opt} = 0 )= 1$ ⇒ $\rho_d (T_{\rm D, \ opt} = 0 ) = 200= \rho _{\rm MF}$.
(3) Es gelten weiter die Einstellungen von (2) mit Ausnahme von $N_0=0.02 $ statt $N_0=0.01$. Welche Veränderungen sind erkennbar?
- Der einzige Unterschied ist die doppelt so große Rauschvarianz $\sigma_d^2= 0.01$ ⇒ $\rho_d (T_{\rm D, \ opt} = 0 ) = 100= \rho _{\rm MF}$ ⇒ $10 \cdot \lg \rho_{\rm MF} =20$ dB.
(4) Es gelten weiter die Einstellungen von (3) mit Ausnahme von $T_{\rm D} = 0.1 $ statt $T_{\rm D, \ opt} = 0$. Wie wirkt sich dieser nichtoptimale Detektionszeitpunkt aus?
- Nun ist der Nutzabtastwert $d_{\rm S} (T_{\rm D} = 0.1 )= 0.9$ kleiner ⇒ $\rho_d (T_{\rm D} = 0.1 ) =0.9^2/0.01= 81< \rho _{\rm MF}$. Es ergibt sich eine Verschlechterung um knapp ein dB.
- Für die weiteren Aufgaben wird vom optimalen Detektionszeitpunkt $T_{\rm D, \ opt}$ ausgegangen, wenn nicht explizit etwas anderes angegeben wird.
(5) Es gelten wieder die Einstellungen von (3) mit Ausnahme einer niedrigeren Impulsantwort $A_h = 0.8 $ statt $A_h = 1$. Interpretieren Sie die Veränderungen.
- Es handelt sich auch mit $A_h \ne A_g$ um ein Matched-Filter, solange $h(t)$ formgleich mit $g(t)$ ist ⇒ $\rho _{\rm MF} = { {2 \cdot E_g } }/{ {N_0 } } =100$ ⇒ $10 \cdot \lg \rho_{\rm MF} =20$ dB.
- Die Gleichung $\rho_d (T_{\rm D}=0) =d_{\rm S}^2 (T_{\rm D}=0)/\sigma_d^2$ führt zum gleichen Ergebnis, da ${d_{\rm S}}^2 (T_{\rm D})$ und $\sigma_d^2$ gegenüber (3) jeweils um den Faktor $0.8^2$ vermindert wird.
(6) Gegenüber (5) wird nun die Höhe des Eingangsimpulses $g(t)$ von $A_g = 1$ auf $A_g = 1.25$ erhöht. Beschreibt hier $h(t)$ ein Matched-Filter? Wie groß ist $\rho_{\rm MF}$?
- Auch hier liegt ein Matched-Filter vor, da $h(t)$ und $g(t)$ formgleich sind. Mit $E_g = 1.25^2$: $\rho _{\rm MF} = { {2 \cdot 1.25^2 } }/{ 0.02 } =156.25$ ⇒ $10 \cdot \lg \rho_{\rm MF} \approx 21.9$ dB.
- Der höhere Wert $21.9$ dB gegenüber (5) lässt sich dadurch erklären, dass bei gleicher Rauschvarianz $\sigma_d^2= 0.0064$ der Nutzabtastwert wieder ${d_{\rm S}} (T_{\rm D}) = 1$ ist.
(7) Wir gehen weiter von der Rechteck–Rechteck–Kombination aus mit $A_h=A_g=1,\ \Delta t_h=\Delta t_g=1,\ \tau_h=\tau_g=0,\ N_0 =0.02,\ T_{\rm D}=0$.
Interpretieren Sie die Ergebnisse nach Variation der äquivalenten Impulsdauer $\Delta t_h$ von $h(t)$ im Bereich $0.6$ ... $1.4$. Nutzen Sie die Grafikdarstellung über $\Delta t_h$.
- Das Optimum ergibt sich erwartungsgemäß für die äquivalente Impulsdauer $\Delta t_h=\Delta t_g=1$. Dann ist $10 \cdot \lg \ \rho_d (T_{\rm D, \ opt} = 0 ) =20$ dB $\big(= 10 \cdot \lg \rho_{\rm MF}\big)$.
- Ist $\Delta t_h<\Delta t_g=1$, so ist das Nutzsignal trapezförmig. Für $\Delta t_h=0.6$: $d_{\rm S} (T_{\rm D}=0)= 0.6$ und $\sigma_d^2\approx0.006$ ⇒ $10 \cdot \lg \ \rho_d (T_{\rm D, \ opt} = 0 ) \approx 17.8$ dB.
- Auch für $\Delta t_h>1$ ist das Nutzsignal trapezförmig, aber trotzdem $d_{\rm S} (T_{\rm D}=0)= 1$. Die Rauschvarianz $\sigma_d^2$ nimmt kontinuierlich mit $\Delta t_h$ zu.
- Für $\Delta t_h=1.4$ ist $\sigma_d^2=0.0140$ ⇒ $10 \cdot \lg \ \rho_d (T_{\rm D, \ opt} = 0 ) \approx 18.5$ dB. Gegenüber dem Matched–Filter $(\Delta t_h=1)$ beträgt die Verschlechterung ca. $1.5$ dB.
(8) Interpretieren Sie nun die Ergebnisse für verschiedene $\Delta t_g$ des Eingangsimpulses $g(t)$ im Bereich $0.6$ ... $1.4$. Nutzen Sie die Grafikdarstellung über $\Delta t_g$.
- Beachten Sie: Die blaue Kurve $10 \cdot \lg \ \rho_d (T_{\rm D,\ opt} )$ ist die Differenz aus $20\cdot \lg \ \big [{K \cdot d_{\rm S}} (T_{\rm D,\ opt}) \big ]$ (violette Kurve) und $20\cdot \lg \ \big [K \cdot \sigma_d \big ]$ (grüne Kurve).
- Beim betrachteten Parametersatz und $K=10$ ist der grüne Term $20\cdot \lg \ \big [K \cdot \sigma_d \big ] = 0$ dB für alle $\Delta t_g$ ⇒ die blaue und die violette Kurve sind identisch.
- Die blaue Kurve $10 \cdot \lg \ \rho_d (T_{\rm D,\ opt} )$ steigt von $15.6$ dB $($für $\Delta t_g = 0.6)$ bis $20$ dB $($für $\Delta t_g = 1)$ kontinuierlich an und bleibt für $\Delta t_g > 1$ dann konstant.
- Die Einstellung $\Delta t_g = 1.4,\ \Delta t_h = 1$ ergibt aber kein Matched-Filter. Vielmehr gilt mit $\Delta t_h = \Delta t_g = 1.4$: $10 \cdot \lg \ \rho_{\rm MF}=10 \cdot \lg \ (2 \cdot E_g/N_0) \approx 21.5$ dB.
- Die Grafikdarstellung über $\Delta t_h$ mit der Grundeinstellung $\Delta t_g = 1.4,\ \Delta t_h = 1$ zeigt nun einen monotonen Anstieg der blauen Kurve $10 \cdot \lg \ \rho_d (T_{\rm D,\ opt} )$.
- Für $\Delta t_h = 0.6$ ergibt sich $10 \cdot \lg \ \rho_d (T_{\rm D,\ opt} )\approx 17.8$ dB, für $\Delta t_h = 1.4$ dagegen $10 \cdot \lg \ \rho_d (T_{\rm D,\ opt} )\approx 21.5$ dB $=10 \cdot \lg \ \rho_{\rm MF}$.
(9) Wir betrachten den Exponentialimpuls $g(t)$ und den Tiefpass erster Ordnung sowie $A_h=A_g=1,\ \Delta t_h=\Delta t_g=1,\ \tau_h=\tau_g=0,\ N_0 =0.02,\ T_{\rm D}=1$.
Erfüllt diese Einstellung den Matched-Filter-Kriterien? Begründen Sie Ihre Antworten mit möglichst vielen Argumenten.
- Hier gilt $h(t)=g(t)$. Bei einer Matched-Filter-Konfiguration müsste $h(t)={\rm const.} \cdot g(T_{\rm D}-t)$ gelten.
- Das Detektionsnutzsignal $d_{\rm S}(t)$ hat keinen symmetrischen Verlauf um das Maximum. Beim Matched-Filter müsste $d_{\rm S}(T_{\rm D}-t) = d_{\rm S}(T_{\rm D}+t) $ gelten.
- Trotz $\Delta t_h=\Delta t_g$ ist $10 \cdot \lg \ \rho_d (T_{\rm D,\ opt}) \approx 14.3$ dB kleiner als $10 \cdot \lg \ \rho _{\rm MF} = 10 \cdot \lg \ 2 \cdot E_g/N_0 \approx 17$ dB.
(10) Was ändert sich bei sonst gleichen Einstellungen mit dem "extrem akausalen Filter"? Erfüllt die Einstellung die Matched-Filter-Kriterien? Begründung.
- Hier gilt nun $h(t)=g(-t)$ und das Detektionsnutzsignal $d_{\rm S}(t)$ ist symmetrisch um $t=0$. Sinnvollerweise sollte hier $T_{\rm D} = 0 $ gewählt werden.
- Damit erhält man für $10 \cdot \lg \ \rho_d (T_{\rm D,\ opt}) =10 \cdot \lg \ d_{\rm S}^2 (T_{\rm D,\ opt})/\sigma_d^2 = 17$ dB den gleichen Wert wie für $10 \cdot \lg \ \rho _{\rm MF} = 10 \cdot \lg \ 2 \cdot E_g/N_0 = 17$ dB.
- Das Nutzsignal $d_{\rm S}(t)$ ist formgleich mit der Energie–AKF des Sendeimulses $g(t)$. Das Matched-Filter bündelt die Energie um den geeigneten Zeitpunkt $T_{\rm D,\ opt}$.
(11) Mit welchem Rechteckimpuls $g(t)$ erreicht man mit dem entsprechend angepassten Filter das gleiche $\rho _{\rm MF}=50$ wie in Aufgabe (10)?
Mit $A_h=A_g=1,\ \Delta t_h=\Delta t_g=0.5$ oder mit $A_h=A_g=0.5,\ \Delta t_h=\Delta t_g=1$ ?
- Aus der Gleichung $\rho _{\rm MF} = 2 \cdot E_g/N_0$ geht bereits hervor, dass das SNR nur von der Energie $E_g$ des Eingangsimpulses abhängt und nicht von dessen Form.
- Der Exponentialimpuls mit $A_g=1,\ \Delta t_g=1$ hat die Energie $E_g=0.5$. Der Rechteckimpuls mit $A_g=1,\ \Delta t_g=0.5$ ebenfalls ⇒ $\rho _{\rm MF}=50$.
- Dagegen besitzt der Rechteckimpuls mit $A_g=0.5,\ \Delta t_g=1$ eine kleinere Energie ⇒ $E_g=0.25$ ⇒ $\rho _{\rm MF}=25$ ⇒ $10 \cdot \lg \ \rho _{\rm MF} = 14$ dB.
Applet Manual
(A) Auswahl eines von vier Quellensignalen
(B) Parameterwahl für Quellensignal $1$ (Amplitude, Frequenz, Phase)
(C) Ausgabe der verwendeten Programmparameter
(D) Parameterwahl für Abtastung $(f_{\rm G})$ und
Signalrekonstruktion $(f_{\rm A},\ r)$
(E) Skizze des Empfänger–Frequenzgangs $H_{\rm E}(f)$
(F) Numerische Ausgabe $(P_x, \ P_{\rm \varepsilon}, \ 10 \cdot \lg(P_x/ P_{\rm \varepsilon})$
(G) Darstellungsauswahl für Zeitbereich
(H) Grafikbereich für Zeitbereich
( I ) Darstellungsauswahl für Frequenzbereich
(J) Grafikbereich für Frequenzbereich
(K) Bereich für Übungen: Aufgabenauswahl, Fragen, Musterlösung
About the Authors
Dieses interaktive Berechnungstool wurde am Lehrstuhl für Nachrichtentechnik der Technischen Universität München konzipiert und realisiert.
- Die erste Version wurde 2006 von Markus Elsberger im Rahmen seiner Diplomarbeit (LB) mit "FlashMX–Actionscript" erstellt (Betreuer: Günter Söder).
- 2020 wurde das Programm von Carolin Mirschina im Rahmen einer Werkstudententätigkeit auf "HTML5" umgesetzt und neu gestaltet (Betreuer: Tasnád Kernetzky).
Die Umsetzung dieses Applets auf HTML 5 wurde durch die Exzellenzinitiative der TU München finanziell unterstützt. Wir bedanken uns.