Difference between revisions of "Aufgaben:Exercise 1.10: BPSK Baseband Model"
| Line 4: | Line 4: | ||
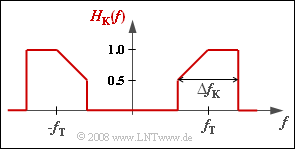
[[File:P_ID1683__Dig_A_4_3.png|right|frame|Unbalanced channel frequency response]] | [[File:P_ID1683__Dig_A_4_3.png|right|frame|Unbalanced channel frequency response]] | ||
| − | In this exercise, we consider a BPSK system with coherent demodulation, i.e. | + | In this exercise, we consider a BPSK system with coherent demodulation, i.e. |
:$$s(t) \ = \ z(t) \cdot q(t),$$ | :$$s(t) \ = \ z(t) \cdot q(t),$$ | ||
:$$b(t) \ = \ 2 \cdot z(t) \cdot r(t) .$$ | :$$b(t) \ = \ 2 \cdot z(t) \cdot r(t) .$$ | ||
| Line 12: | Line 12: | ||
:$$H_{\rm MKD}(f) = {1}/{2} \cdot \big [ H_{\rm K}(f-f_{\rm T}) + H_{\rm K}(f+f_{\rm T})\big ] .$$ | :$$H_{\rm MKD}(f) = {1}/{2} \cdot \big [ H_{\rm K}(f-f_{\rm T}) + H_{\rm K}(f+f_{\rm T})\big ] .$$ | ||
| − | *Thus the modulator and demodulator are virtually shortened against each other, | + | *Thus the modulator and demodulator are virtually shortened against each other, and |
| − | |||
| + | *the bandpass channel $H_{\rm K}(f)$ is transformed into the low-pass range. | ||
| − | |||
| − | + | The resulting transmission function $H_{\rm MKD}(f)$ should not be confused with the low-pass transmission function $H_{\rm K, \, TP}(f)$ as described in the chapter [[Signal_Representation/Equivalent_Low-Pass_Signal_and_its_Spectral_Function|"Equivalent Low-Pass Signal and its Spectral Function"]] of the book "Signal Representation", which results from $H_{\rm K}(f)$ by truncating the components at negative frequencies as well as a frequency shift by the carrier frequency $f_{\rm T}$ to the left. | |
| + | For frequency responses, in contrast to spectral functions, the doubling of the components at positive frequencies must be omitted. | ||
| + | Notes: | ||
| + | *The exercise belongs to the chapter [[Digital_Signal_Transmission/Linear_Digital_Modulation_-_Coherent_Demodulation|"Linear Digital Modulation - Coherent Demodulation"]]. | ||
| − | + | *Reference is made in particular to the section [[Digital_Signal_Transmission/Linear_Digital_Modulation_-_Coherent_Demodulation#Baseband_model_for_ASK_and_BPSK|"Baseband model for ASK and BPSK"]]. | |
| − | + | ||
| − | *Reference is made in particular to the section [[Digital_Signal_Transmission/Linear_Digital_Modulation_-_Coherent_Demodulation#Baseband_model_for_ASK_and_BPSK|Baseband model for ASK and BPSK]]. | + | *The subscript "MKD" stands for "modulator – channel – demodulator" German: "Modulator – Kanal – Demodulator"). |
| Line 36: | Line 38: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Which statements are valid for the equivalent | + | {Which statements are valid for the equivalent low-pass function $H_{\rm K, \, TP}(f)$ ? |
|type="[]"} | |type="[]"} | ||
| − | - $H_{\rm K, \, TP}(f=0)= 2$ | + | - $H_{\rm K, \, TP}(f=0)= 2$. |
| − | + $H_{\rm K, \, TP}(f = \Delta f_{\rm K}/4) = 1$ | + | + $H_{\rm K, \, TP}(f = \Delta f_{\rm K}/4) = 1$. |
| − | + $H_{\rm K, \, TP}(f = | + | + $H_{\rm K, \, TP}(f = -\Delta f_{\rm K}/4) = 0.75$. |
+ The corresponding time function $h_{\rm K, \, TP}(t)$ is complex. | + The corresponding time function $h_{\rm K, \, TP}(t)$ is complex. | ||
{Which statements are valid for the frequency response $H_{\rm MKD}(f)$ ? | {Which statements are valid for the frequency response $H_{\rm MKD}(f)$ ? | ||
|type="[]"} | |type="[]"} | ||
| − | - $H_{\rm MKD}(f=0)= 2$ | + | - $H_{\rm MKD}(f=0)= 2$. |
| − | - $H_{\rm MKD}(f = \Delta f_{\rm K}/4) = 1$ | + | - $H_{\rm MKD}(f = \Delta f_{\rm K}/4) = 1$. |
| − | + $H_{\rm MKD}(f = | + | + $H_{\rm MKD}(f = -\Delta f_{\rm K}/4) = 0.75$. |
- The corresponding time function $h_{\rm MKD}(t)$ is complex. | - The corresponding time function $h_{\rm MKD}(t)$ is complex. | ||
| − | {Calculate the time function $h_{\rm MKD}(t)$. Specify the value at $t = 0$. | + | {Calculate the time function $h_{\rm MKD}(t)$. Specify the value at $t = 0$. |
|type="{}"} | |type="{}"} | ||
$ h_{\rm MKD}(t = 0)/\Delta f_{\rm K} \ = \ $ { 0.75 3% } | $ h_{\rm MKD}(t = 0)/\Delta f_{\rm K} \ = \ $ { 0.75 3% } | ||
Revision as of 14:40, 7 May 2022
In this exercise, we consider a BPSK system with coherent demodulation, i.e.
- $$s(t) \ = \ z(t) \cdot q(t),$$
- $$b(t) \ = \ 2 \cdot z(t) \cdot r(t) .$$
The designations chosen here are based on the block diagram in the theory section.
The influence of a channel frequency response $H_{\rm K}(f)$ can be taken into account in a simple way if it is described together with modulator and demodulator by a common baseband frequency response:
- $$H_{\rm MKD}(f) = {1}/{2} \cdot \big [ H_{\rm K}(f-f_{\rm T}) + H_{\rm K}(f+f_{\rm T})\big ] .$$
- Thus the modulator and demodulator are virtually shortened against each other, and
- the bandpass channel $H_{\rm K}(f)$ is transformed into the low-pass range.
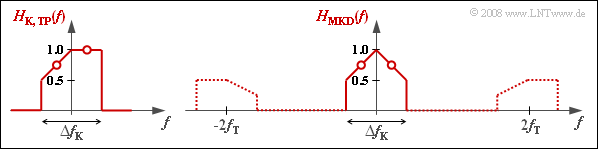
The resulting transmission function $H_{\rm MKD}(f)$ should not be confused with the low-pass transmission function $H_{\rm K, \, TP}(f)$ as described in the chapter "Equivalent Low-Pass Signal and its Spectral Function" of the book "Signal Representation", which results from $H_{\rm K}(f)$ by truncating the components at negative frequencies as well as a frequency shift by the carrier frequency $f_{\rm T}$ to the left.
For frequency responses, in contrast to spectral functions, the doubling of the components at positive frequencies must be omitted.
Notes:
- The exercise belongs to the chapter "Linear Digital Modulation - Coherent Demodulation".
- Reference is made in particular to the section "Baseband model for ASK and BPSK".
- The subscript "MKD" stands for "modulator – channel – demodulator" German: "Modulator – Kanal – Demodulator").
Questions
Solution
- $H_{\rm K,TP}(f)$ results from $H_{\rm K}(f)$ by cutting off the negative frequency components and shifting $f_{\rm T}$ to the left.
- For frequency responses – in contrast to spectra – the doubling of the components at positive frequencies is omitted. Therefore:
- $$H_{\rm K,\hspace{0.04cm} TP}(f= 0) = H_{\rm K}(f= f_{\rm T})=1.$$
- Because of the real and asymmetrical spectral functions $H_{\rm K,\hspace{0.04cm}TP}(f)$ the corresponding time function (Fourier inverse transform) $h_{\rm K,\hspace{0.04cm}TP}(t)$ is complex according to the allocation theorem.
(2) Here only the third proposed solution is correct:
- The spectral function $H_{\rm MKD}(f)$ always has an even real part and no imaginary part. Consequently $h_{\rm MKD}(t)$ is always real.
- If $H_{\rm K}(f)$ had additionally an imaginary part odd by $f_{\rm T}$, $H_{\rm MKD}(f)$ would have an imaginary part odd by $f = 0$. Thus $h_{\rm MKD}(t)$ would still be a real function.
The diagram illustrates the differences between $H_{\rm K,\hspace{0.04cm}TP}(f)$ and $H_{\rm MKD}(f)$. The parts of $H_{\rm MKD}(f)$ in the range around $\pm 2f_{\rm T}$ need not be considered further.
(3) $H_{\rm MKD}(f)$ is additively composed of a rectangle and a triangle, each with width $\Delta f_{\rm K}$ and height $0.5$. It follows:
- $$h_{\rm MKD}(t) = \frac{\Delta f_{\rm K}}{2} \cdot {\rm si} (\pi \cdot \Delta f_{\rm K} \cdot t)+ \frac{\Delta f_{\rm K}}{4} \cdot {\rm si}^2 (\pi \cdot \frac{\Delta f_{\rm K}}{2} \cdot t)$$
- $$ \Rightarrow \hspace{0.3cm}h_{\rm MKD}(t = 0) = \frac{\Delta f_{\rm K}}{2} + \frac{\Delta f_{\rm K}}{4} = 0.75 \cdot \Delta f_{\rm K}\hspace{0.3cm} \Rightarrow \hspace{0.3cm}h_{\rm MKD}(t = 0)/{\Delta f_{\rm K}} \hspace{0.1cm}\underline {= 0.75} .$$
(4) The second proposed solution is correct:
- The first si function does have equidistant zero crossings at the distance $1/\Delta f_{\rm K}$.
- But the equidistant zero crossings of the whole time function $h_{\rm MKD}$ are determined by the second term:
- $$h_{\rm MKD}(t = \frac{1}{\Delta f_{\rm K}}) = \ \frac{\Delta f_{\rm K}}{2} \cdot {\rm si} (\pi )+ \frac{\Delta f_{\rm K}}{4} \cdot {\rm si}^2 (\pi/2) = \frac{\Delta f_{\rm K}}{4},$$
- $$h_{\rm MKD}(t = \frac{2}{\Delta f_{\rm K}}) = \ \frac{\Delta f_{\rm K}}{2} \cdot {\rm si} (2\pi )+ \frac{\Delta f_{\rm K}}{4} \cdot {\rm si}^2 (\pi) = 0.$$