Difference between revisions of "Aufgaben:Exercise 1.10: BPSK Baseband Model"
m (Text replacement - "Category:Aufgaben zu Digitalsignalübertragung" to "Category:Digital Signal Transmission: Exercises") |
|||
| (5 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Digital_Signal_Transmission/Linear_Digital_Modulation_-_Coherent_Demodulation |
}} | }} | ||
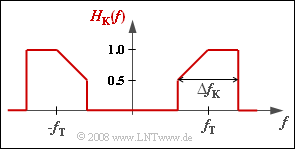
| − | [[File:P_ID1683__Dig_A_4_3.png|right|frame| | + | [[File:P_ID1683__Dig_A_4_3.png|right|frame|Unbalanced channel frequency response]] |
| − | + | In this exercise, we consider a BPSK system with coherent demodulation, i.e. | |
:$$s(t) \ = \ z(t) \cdot q(t),$$ | :$$s(t) \ = \ z(t) \cdot q(t),$$ | ||
:$$b(t) \ = \ 2 \cdot z(t) \cdot r(t) .$$ | :$$b(t) \ = \ 2 \cdot z(t) \cdot r(t) .$$ | ||
| − | + | The designations chosen here are based on the [[Digital_Signal_Transmission/Linear_Digital_Modulation_-_Coherent_Demodulation#Common_block_diagram_for_ASK_and_BPSK|"block diagram"]] in the theory section. | |
| − | + | The influence of a channel frequency response $H_{\rm K}(f)$ can be taken into account in a simple way if it is described together with modulator and demodulator by a common baseband frequency response: | |
:$$H_{\rm MKD}(f) = {1}/{2} \cdot \big [ H_{\rm K}(f-f_{\rm T}) + H_{\rm K}(f+f_{\rm T})\big ] .$$ | :$$H_{\rm MKD}(f) = {1}/{2} \cdot \big [ H_{\rm K}(f-f_{\rm T}) + H_{\rm K}(f+f_{\rm T})\big ] .$$ | ||
| − | * | + | *Thus the modulator and demodulator are virtually shortened against each other, and |
| − | |||
| + | *the band-pass channel $H_{\rm K}(f)$ is transformed into the low-pass range. | ||
| − | |||
| − | + | The resulting transmission function $H_{\rm MKD}(f)$ should not be confused with the low-pass transmission function $H_{\rm K, \, TP}(f)$ as described in the chapter [[Signal_Representation/Equivalent_Low-Pass_Signal_and_its_Spectral_Function|"Equivalent Low-Pass Signal and its Spectral Function"]] of the book "Signal Representation", which results from $H_{\rm K}(f)$ by truncating the components at negative frequencies as well as a frequency shift by the carrier frequency $f_{\rm T}$ to the left. | |
| + | For frequency responses, in contrast to spectral functions, the doubling of the components at positive frequencies must be omitted. | ||
| + | Notes: | ||
| + | *The exercise belongs to the chapter [[Digital_Signal_Transmission/Linear_Digital_Modulation_-_Coherent_Demodulation|"Linear Digital Modulation - Coherent Demodulation"]]. | ||
| − | + | *Reference is made in particular to the section [[Digital_Signal_Transmission/Linear_Digital_Modulation_-_Coherent_Demodulation#Baseband_model_for_ASK_and_BPSK|"Baseband model for ASK and BPSK"]]. | |
| − | * | + | |
| − | * | + | *The subscript "MKD" stands for "modulator – channel – demodulator" German: "Modulator – Kanal – Demodulator"). |
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Which statements are valid for the equivalent low-pass function $H_{\rm K, \, TP}(f)$ ? |
|type="[]"} | |type="[]"} | ||
| − | - | + | - $H_{\rm K, \, TP}(f=0)= 2$. |
| − | + | + | + $H_{\rm K, \, TP}(f = \Delta f_{\rm K}/4) = 1$. |
| − | + | + | + $H_{\rm K, \, TP}(f = -\Delta f_{\rm K}/4) = 0.75$. |
| − | + | + | + The corresponding time function $h_{\rm K, \, TP}(t)$ is complex. |
| − | { | + | {Which statements are valid for the frequency response $H_{\rm MKD}(f)$ ? |
|type="[]"} | |type="[]"} | ||
| − | - | + | - $H_{\rm MKD}(f=0)= 2$. |
| − | - | + | - $H_{\rm MKD}(f = \Delta f_{\rm K}/4) = 1$. |
| − | + | + | + $H_{\rm MKD}(f = -\Delta f_{\rm K}/4) = 0.75$. |
| − | - | + | - The corresponding time function $h_{\rm MKD}(t)$ is complex. |
| − | { | + | {Calculate the time function $h_{\rm MKD}(t)$. Specify the value at $t = 0$. |
|type="{}"} | |type="{}"} | ||
$ h_{\rm MKD}(t = 0)/\Delta f_{\rm K} \ = \ $ { 0.75 3% } | $ h_{\rm MKD}(t = 0)/\Delta f_{\rm K} \ = \ $ { 0.75 3% } | ||
| − | { | + | {Which of the following statements are true? |
|type="[]"} | |type="[]"} | ||
| − | -$h_{\rm MKD}(t)$ | + | -$h_{\rm MKD}(t)$ has equidistant zero crossings at distance $1/\Delta f_{\rm K}$. |
| − | +$h_{\rm MKD}(t)$ | + | +$h_{\rm MKD}(t)$ has equidistant zero crossings at distance $2/\Delta f_{\rm K}$. |
| Line 63: | Line 65: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' <u>Statements 2, 3 and 4</u> are correct: |
| − | *$H_{\rm K,TP}(f)$ | + | *$H_{\rm K,TP}(f)$ results from $H_{\rm K}(f)$ by cutting off the negative frequency components and shifting $f_{\rm T}$ to the left. |
| − | * | + | |
| + | * For frequency responses – in contrast to spectra – the doubling of the components at positive frequencies is omitted. Therefore: | ||
:$$H_{\rm K,\hspace{0.04cm} TP}(f= 0) = H_{\rm K}(f= f_{\rm T})=1.$$ | :$$H_{\rm K,\hspace{0.04cm} TP}(f= 0) = H_{\rm K}(f= f_{\rm T})=1.$$ | ||
| − | * | + | *Because of the real and asymmetrical spectral functions $H_{\rm K,\hspace{0.04cm}TP}(f),$ the corresponding time function (inverse Fourier transform) $h_{\rm K,\hspace{0.04cm}TP}(t)$ is complex according to the "Allocation Theorem". |
| + | |||
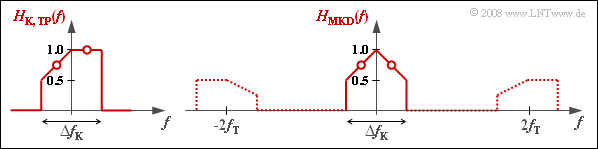
| + | [[File:P_ID1684__Dig_A_4_3_a.png|right|frame|Low-pass functions for $H_{\rm K}(f)$]] | ||
| − | + | '''(2)''' Here only the <u>third proposed solution</u> is correct: | |
| + | *The spectral function $H_{\rm MKD}(f)$ always has an even real part and no imaginary part. Consequently $h_{\rm MKD}(t)$ is always real. | ||
| − | + | *If $H_{\rm K}(f)$ had additionally an imaginary part odd by $f= f_{\rm T}$, $H_{\rm MKD}(f)$ would have an imaginary part odd by $f = 0$. Thus $h_{\rm MKD}(t)$ would still be a real function. | |
| − | |||
| − | |||
| − | + | The diagram illustrates the differences between $H_{\rm K,\hspace{0.04cm}TP}(f)$ and $H_{\rm MKD}(f)$. The parts of $H_{\rm MKD}(f)$ in the range around $\pm 2f_{\rm T}$ need not be considered further. | |
| − | '''(3)''' $H_{\rm MKD}(f)$ | + | '''(3)''' $H_{\rm MKD}(f)$ is additively composed of a rectangle and a triangle, each with width $\Delta f_{\rm K}$ and height $0.5$. It follows: |
| − | :$$h_{\rm MKD}(t) = \frac{\Delta f_{\rm K}}{2} \cdot {\rm | + | :$$h_{\rm MKD}(t) = \frac{\Delta f_{\rm K}}{2} \cdot {\rm sinc} ( \Delta f_{\rm K} \cdot t)+ \frac{\Delta f_{\rm K}}{4} \cdot {\rm sinc}^2 ( \frac{\Delta f_{\rm K}}{2} \cdot t)$$ |
:$$ \Rightarrow \hspace{0.3cm}h_{\rm MKD}(t = 0) = \frac{\Delta f_{\rm K}}{2} + \frac{\Delta f_{\rm K}}{4} = 0.75 \cdot \Delta f_{\rm K}\hspace{0.3cm} | :$$ \Rightarrow \hspace{0.3cm}h_{\rm MKD}(t = 0) = \frac{\Delta f_{\rm K}}{2} + \frac{\Delta f_{\rm K}}{4} = 0.75 \cdot \Delta f_{\rm K}\hspace{0.3cm} | ||
\Rightarrow \hspace{0.3cm}h_{\rm MKD}(t = 0)/{\Delta f_{\rm K}} \hspace{0.1cm}\underline {= 0.75} .$$ | \Rightarrow \hspace{0.3cm}h_{\rm MKD}(t = 0)/{\Delta f_{\rm K}} \hspace{0.1cm}\underline {= 0.75} .$$ | ||
| − | '''(4)''' | + | '''(4)''' The <u>second proposed solution</u> is correct: |
| − | * | + | *The first sinc–function does have equidistant zero crossings at the distance $1/\Delta f_{\rm K}$. |
| − | * | + | *But the equidistant zero crossings of the whole time function $h_{\rm MKD}(t)$ are determined by the second term: |
| − | :$$h_{\rm MKD}(t = \frac{1}{\Delta f_{\rm K}}) = \ \frac{\Delta f_{\rm K}}{2} \cdot {\rm | + | :$$h_{\rm MKD}(t = \frac{1}{\Delta f_{\rm K}}) = \ \frac{\Delta f_{\rm K}}{2} \cdot {\rm sinc} (1 )+ |
| − | \frac{\Delta f_{\rm K}}{4} \cdot {\rm | + | \frac{\Delta f_{\rm K}}{4} \cdot {\rm sinc}^2 (0.5) = \frac{\Delta |
f_{\rm K}}{4},$$ | f_{\rm K}}{4},$$ | ||
:$$h_{\rm MKD}(t = \frac{2}{\Delta f_{\rm K}}) = \ \frac{\Delta | :$$h_{\rm MKD}(t = \frac{2}{\Delta f_{\rm K}}) = \ \frac{\Delta | ||
| − | f_{\rm K}}{2} \cdot {\rm | + | f_{\rm K}}{2} \cdot {\rm sinc} (2 )+ \frac{\Delta f_{\rm K}}{4} |
| − | \cdot {\rm | + | \cdot {\rm sinc}^2 (1) = 0.$$ |
| Line 104: | Line 108: | ||
| − | [[Category:Digital Signal Transmission: Exercises|^1.5 | + | [[Category:Digital Signal Transmission: Exercises|^1.5 Linear Digital Modulation^]] |
Latest revision as of 17:15, 10 May 2022
In this exercise, we consider a BPSK system with coherent demodulation, i.e.
- $$s(t) \ = \ z(t) \cdot q(t),$$
- $$b(t) \ = \ 2 \cdot z(t) \cdot r(t) .$$
The designations chosen here are based on the "block diagram" in the theory section.
The influence of a channel frequency response $H_{\rm K}(f)$ can be taken into account in a simple way if it is described together with modulator and demodulator by a common baseband frequency response:
- $$H_{\rm MKD}(f) = {1}/{2} \cdot \big [ H_{\rm K}(f-f_{\rm T}) + H_{\rm K}(f+f_{\rm T})\big ] .$$
- Thus the modulator and demodulator are virtually shortened against each other, and
- the band-pass channel $H_{\rm K}(f)$ is transformed into the low-pass range.
The resulting transmission function $H_{\rm MKD}(f)$ should not be confused with the low-pass transmission function $H_{\rm K, \, TP}(f)$ as described in the chapter "Equivalent Low-Pass Signal and its Spectral Function" of the book "Signal Representation", which results from $H_{\rm K}(f)$ by truncating the components at negative frequencies as well as a frequency shift by the carrier frequency $f_{\rm T}$ to the left.
For frequency responses, in contrast to spectral functions, the doubling of the components at positive frequencies must be omitted.
Notes:
- The exercise belongs to the chapter "Linear Digital Modulation - Coherent Demodulation".
- Reference is made in particular to the section "Baseband model for ASK and BPSK".
- The subscript "MKD" stands for "modulator – channel – demodulator" German: "Modulator – Kanal – Demodulator").
Questions
Solution
- $H_{\rm K,TP}(f)$ results from $H_{\rm K}(f)$ by cutting off the negative frequency components and shifting $f_{\rm T}$ to the left.
- For frequency responses – in contrast to spectra – the doubling of the components at positive frequencies is omitted. Therefore:
- $$H_{\rm K,\hspace{0.04cm} TP}(f= 0) = H_{\rm K}(f= f_{\rm T})=1.$$
- Because of the real and asymmetrical spectral functions $H_{\rm K,\hspace{0.04cm}TP}(f),$ the corresponding time function (inverse Fourier transform) $h_{\rm K,\hspace{0.04cm}TP}(t)$ is complex according to the "Allocation Theorem".
(2) Here only the third proposed solution is correct:
- The spectral function $H_{\rm MKD}(f)$ always has an even real part and no imaginary part. Consequently $h_{\rm MKD}(t)$ is always real.
- If $H_{\rm K}(f)$ had additionally an imaginary part odd by $f= f_{\rm T}$, $H_{\rm MKD}(f)$ would have an imaginary part odd by $f = 0$. Thus $h_{\rm MKD}(t)$ would still be a real function.
The diagram illustrates the differences between $H_{\rm K,\hspace{0.04cm}TP}(f)$ and $H_{\rm MKD}(f)$. The parts of $H_{\rm MKD}(f)$ in the range around $\pm 2f_{\rm T}$ need not be considered further.
(3) $H_{\rm MKD}(f)$ is additively composed of a rectangle and a triangle, each with width $\Delta f_{\rm K}$ and height $0.5$. It follows:
- $$h_{\rm MKD}(t) = \frac{\Delta f_{\rm K}}{2} \cdot {\rm sinc} ( \Delta f_{\rm K} \cdot t)+ \frac{\Delta f_{\rm K}}{4} \cdot {\rm sinc}^2 ( \frac{\Delta f_{\rm K}}{2} \cdot t)$$
- $$ \Rightarrow \hspace{0.3cm}h_{\rm MKD}(t = 0) = \frac{\Delta f_{\rm K}}{2} + \frac{\Delta f_{\rm K}}{4} = 0.75 \cdot \Delta f_{\rm K}\hspace{0.3cm} \Rightarrow \hspace{0.3cm}h_{\rm MKD}(t = 0)/{\Delta f_{\rm K}} \hspace{0.1cm}\underline {= 0.75} .$$
(4) The second proposed solution is correct:
- The first sinc–function does have equidistant zero crossings at the distance $1/\Delta f_{\rm K}$.
- But the equidistant zero crossings of the whole time function $h_{\rm MKD}(t)$ are determined by the second term:
- $$h_{\rm MKD}(t = \frac{1}{\Delta f_{\rm K}}) = \ \frac{\Delta f_{\rm K}}{2} \cdot {\rm sinc} (1 )+ \frac{\Delta f_{\rm K}}{4} \cdot {\rm sinc}^2 (0.5) = \frac{\Delta f_{\rm K}}{4},$$
- $$h_{\rm MKD}(t = \frac{2}{\Delta f_{\rm K}}) = \ \frac{\Delta f_{\rm K}}{2} \cdot {\rm sinc} (2 )+ \frac{\Delta f_{\rm K}}{4} \cdot {\rm sinc}^2 (1) = 0.$$