Difference between revisions of "Aufgaben:Exercise 1.3: Calculating with Complex Numbers"
From LNTwww
| Line 9: | Line 9: | ||
:$$z_3 = -{\rm j} .$$ | :$$z_3 = -{\rm j} .$$ | ||
| − | In the course of this task, the following complex | + | In the course of this task, the following complex values will be considered: |
:$$z_4 = z_2^2 + z_3^2,$$ | :$$z_4 = z_2^2 + z_3^2,$$ | ||
:$$z_5 = 1/z_2,$$ | :$$z_5 = 1/z_2,$$ | ||
| Line 28: | Line 28: | ||
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| Line 35: | Line 35: | ||
+ <math>2 \cdot z_1 + z_2 =0.</math> | + <math>2 \cdot z_1 + z_2 =0.</math> | ||
+ <math>z_1^{\ast} \cdot z_2 +2=0.</math> | + <math>z_1^{\ast} \cdot z_2 +2=0.</math> | ||
| − | - <math>(z_1/z_2) \cdot z_3</math> | + | - <math>(z_1/z_2) \cdot z_3</math> is purely real. |
| − | { | + | {What is the value of the random variable <math>z_4 = z_2^2 + z_3^2 = x_4 + {\rm j} \cdot y_4</math>? |
|type="{}"} | |type="{}"} | ||
<math> x_4 \ =\ </math> { -1.01--0.99 } | <math> x_4 \ =\ </math> { -1.01--0.99 } | ||
| Line 44: | Line 44: | ||
| − | { | + | {Calculate the complex value <math>z_5 = 1/z_2 = x_5 + {\rm j} \cdot y_5</math>. |
|type="{}"} | |type="{}"} | ||
<math> x_5 \ =\ </math> { -0.36--0.35 } | <math> x_5 \ =\ </math> { -0.36--0.35 } | ||
<math> y_5 \ =\ </math> { -0.36--0.35 } | <math> y_5 \ =\ </math> { -0.36--0.35 } | ||
| − | {<math>z_6</math> | + | {<math>z_6</math> is the square root of <math>z_3</math> . Therefore <math>z_6</math> has two solutions with the absolute value <math>|z_6| = 1</math>. <br>Give the two possible phase angles of <math>z_6</math> . |
|type="{}"} | |type="{}"} | ||
| − | <math> \phi_6 \ ({\rm | + | <math> \phi_6 \ ({\rm between\hspace{0.1cm} 0^{\circ} \hspace{0.1cm}and \hspace{0.1cm} +\hspace{-0.15cm}180^{\circ} \hspace{0.1cm}deg}) \hspace{0.2cm} =\ </math> { 133-137 } $\ \text{deg}$ |
| − | <math> \phi_6 \ ({\rm | + | <math> \phi_6 \ ({\rm between\hspace{0.1cm} - \hspace{-0.15cm}180^{\circ} \hspace{0.1cm}and \hspace{0.1cm} 0^{\circ} \hspace{0.1cm}deg}) \hspace{0.2cm} =\ </math> { -47--43 } $\ \text{deg}$ |
| − | { | + | {Calculate <math>z_7 = {\rm e}^{z_2} = x_7 + {\rm j} \cdot y_7</math>. |
|type="{}"} | |type="{}"} | ||
<math> x_7 \ =\ </math> { 0.03-0.04 } | <math> x_7 \ =\ </math> { 0.03-0.04 } | ||
| Line 61: | Line 61: | ||
| − | { | + | {Compute the complex value <math>z_8 = {\rm e}^{z_2} + {\rm e}^{z_2^{\ast}} = x_8 + {\rm j}\cdot y_8</math> . |
|type="{}"} | |type="{}"} | ||
<math> x_8 \ =\ </math> { 0.07-0.08 } | <math> x_8 \ =\ </math> { 0.07-0.08 } | ||
| Line 69: | Line 69: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' Correct are the<u> solutions 1 and 2</u>: |
*Entsprechend den Angaben gilt mit dem [[Signal_Representation/Calculating_With_Complex_Numbers#Darstellung_nach_Betrag_und_Phase|Satz von Euler]]: | *Entsprechend den Angaben gilt mit dem [[Signal_Representation/Calculating_With_Complex_Numbers#Darstellung_nach_Betrag_und_Phase|Satz von Euler]]: | ||
Revision as of 15:39, 25 December 2020
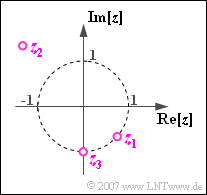
The diagram to the right shows some points in the complex plane, namely
- $$z_1 = {\rm e}^{\hspace{0.05cm}-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 45^{ \circ}}, $$
- $$z_2 = 2 \cdot{\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}135^{ \circ}},$$
- $$z_3 = -{\rm j} .$$
In the course of this task, the following complex values will be considered:
- $$z_4 = z_2^2 + z_3^2,$$
- $$z_5 = 1/z_2,$$
- $$z_6 = \sqrt{z_3},$$
- $$z_7 = {\rm e}^{\hspace{0.05cm}z_2},$$
- $$z_8 = {\rm e}^{\hspace{0.05cm}z_2} + {\rm e}^{\hspace{0.05cm}z_2^{\star}}.$$
Notes:
- This exercise belongs to the chapter Calculating With Complex Numbers.
- The topic is also covered in the teaching video Rechnen mit komplexen Zahlen .
Questions
Solution
(1) Correct are the solutions 1 and 2:
- Entsprechend den Angaben gilt mit dem Satz von Euler:
- \[2 \cdot z_1 + z_2 = 2 \cdot \cos(45^{ \circ}) - 2 \cdot {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} \sin(45^{ \circ})- 2 \cdot \cos(45^{ \circ}) + 2\cdot {\rm j} \cdot\sin(45^{ \circ}) = 0.\]
- Der zweite Vorschlag ist ebenfalls richtig, da
- \[z_1^{\star} \cdot z_2 = 1 \cdot{\rm e}^{{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} 45^{ \circ}} \cdot 2 \cdot{\rm e}^{{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} 135^{ \circ}} = 2 \cdot{\rm e}^{{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} 180^{ \circ}}= -2.\]
- Dagegen ist der dritte Vorschlag falsch. Die Division von \(z_1\) und \(z_2\) liefert:
- \[\frac{z_1}{z_2} = \frac{{\rm e}^{-{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} 45^{ \circ}}}{2 \cdot{\rm e}^{{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}135^{ \circ}}} = 0.5 \cdot{\rm e}^{-{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} 180^{ \circ}}= -0.5.\]
- Die Multiplikation mit \(z_3 = -{\rm j} \) führt zum Ergebnis ${\rm j}/2$, also zu einer rein imaginären Größe.
(2) Das Quadrat von \(z_2\) hat den Betrag \(|z_2|^{2}\) und die Phase \(2 \cdot \phi_2\):
- \[z_2^2 = 2^2 \cdot{\rm e}^{{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} 270^{ \circ}}= 4 \cdot {\rm e}^{-{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} 90^{ \circ}}=-4 \cdot {\rm j}.\]
- Entsprechend gilt für das Quadrat von \(z_3\):
- \[z_3^2 = (-{\rm j})^2 = -1.\]
- Somit ist \(x_4 =\underline{ –1}\) und \(y_4 = \underline{–4}.\)
(3) Durch Anwendung der Divisionsregel erhält man:
- \[z_5 = {1}/{z_2} = \frac{1}{2 \cdot{\rm e}^{{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} 135^{ \circ}}}= 0.5 \cdot{\rm e}^{-{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} 135^{ \circ}} = 0.5 \cdot \big[ \cos (- 135^{ \circ}) + {\rm j} \cdot \sin (- 135^{ \circ})\big]\]
- \[\Rightarrow \ x_5 = - {\sqrt{2}}/{4}\hspace{0.15cm}\underline{= -0.354},\hspace{0.5cm} y_5 = x_5 \hspace{0.15cm}\underline{= -0.354}.\]
(4) Die angegeben Beziehung für \(z_6\) kann wie folgt umgeformt werden: \(z_6^2 = {z_3} = {\rm e}^{-{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} 90^{ \circ}}.\)
- Man erkennt, dass es zwei Möglichkeiten für \(z_6\) gibt, die diese Gleichung erfüllen:
- \[z_6 \hspace{0.1cm}{\rm (1.\hspace{0.1cm} L\ddot{o}sung)}\hspace{0.1cm} = \frac{z_2}{2} = 1 \cdot {\rm e}^{{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}135^{ \circ}} \hspace{0.2cm}\Rightarrow \hspace{0.2cm} \phi_6 \hspace{0.15cm}\underline{= 135^{ \circ}}, \]
- \[z_6 \hspace{0.1cm}{\rm (2.\hspace{0.1cm} L \ddot{o}sung)}\hspace{0.1cm} = {z_1} = 1 \cdot {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}45^{ \circ}} \hspace{0.2cm}\Rightarrow \hspace{0.2cm} \phi_6 \hspace{0.15cm}\underline{=-45^{ \circ}}.\]
(5) Die komplexe Größe \(z_2\) lautet in Realteil/Imaginärteildarstellung:
- \[z_2 = x_2 + {\rm j} \cdot y_2 = -\sqrt{2} + {\rm j} \cdot\sqrt{2}.\]
- Damit ergibt sich für die komplexe Exponentialfunktion:
- \[z_7 = {\rm e}^{-\sqrt{2} + {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}\sqrt{2}}= {\rm e}^{-\sqrt{2} } \cdot \big[ \cos (\sqrt{2}) + {\rm j} \cdot \sin (\sqrt{2})\big].\]
- Mit \({\rm e}^{-\sqrt{2} } = 0.243, \hspace{0.4cm} \cos (\sqrt{2}) = 0.156, \hspace{0.4cm} \sin (\sqrt{2}) = 0.988\) erhält man somit:
- \[z_7 = 0.243 \cdot \left( 0.156 + {\rm j} \cdot 0.988\right) \hspace{0.15cm}\underline{= 0.038 + {\rm j} \cdot 0.24}.\]
(6) Ausgehend vom Ergebnis der Teilaufgabe (4) erhält man für \(z_8\):
- \[z_8 = {\rm e}^{-\sqrt{2} } \cdot \big[ \cos (\sqrt{2}) + {\rm j} \cdot \sin (\sqrt{2}) + \cos (\sqrt{2}) - {\rm j} \cdot \sin (\sqrt{2})\big] = 2 \cdot {\rm e}^{-\sqrt{2} } \cdot \cos (\sqrt{2}) = 2 \cdot x_7 \hspace{0.5cm}\Rightarrow \hspace{0.5cm} x_8 \hspace{0.15cm}\underline{= 0.076}, \hspace{0.4cm}y_8\hspace{0.15cm}\underline{ = 0}.\]