Difference between revisions of "Aufgaben:Exercise 1.6: Rectangular-in-Time Low-Pass Filter"
From LNTwww
| (45 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Linear_and_Time_Invariant_Systems/Some_Low-Pass_Functions_in_Systems_Theory}} |
| − | [[File:P_ID858__LZI_A_1_6.png|right| | + | [[File:P_ID858__LZI_A_1_6.png|right|frame|Rectangular impulse response, non-causal and causal]] |
| − | + | We consider below the constellation shown in the graph: | |
| + | *The frequency response $H(f) = H_1(f) · H_2(f)$ in the lower branch is determined by the impulse responses of its two subcomponents. | ||
| + | *Here, $h_1(t)$ is constantly equal to $k$ in the reange from $-1\ \rm ms$ to $+1\ \rm ms$ and zero outside. | ||
| + | *At the range limits, half the value is valid in each case. | ||
| + | *The time variable drawn in the figure is thus $Δt = 2 \ \rm ms$. | ||
| − | + | The impulse response of the second system function $H_2(f)$ is: | |
| − | $$h_2(t) = \delta(t - \tau).$$ | + | :$$h_2(t) = \delta(t - \tau).$$ |
| − | + | The frequency response between the signals $x(t)$ and $z(t)$ is of high-pass character and generally: | |
| − | $$H_{\rm HP}(f) = 1 - H_1(f) \cdot {\rm e}^{-{\rm | + | :$$H_{\rm HP}(f) = 1 - H_1(f) \cdot {\rm e}^{-{\rm j\hspace{0.05cm}\cdot \hspace{0.05cm}2 \pi}f \tau}.$$ |
| − | + | *For the subtasks '''(1)''' to '''(4)''' the following holds: $τ = 0$ ⇒ $H(f) = H_1(f)$. | |
| − | $$H_{\rm HP}(f) = 1 - {\rm si}( \pi \cdot {\rm \Delta}t \cdot f).$$ | + | *However, using $τ = 0$ this can also be formulated as follows $(Δt = 2 \ \rm ms)$: |
| − | + | :$$H_{\rm HP}(f) = 1 - {\rm si}( \pi \cdot {\rm \Delta}t \cdot f).$$ | |
| − | $$|H_{\rm HP}(f)|\hspace{0.09cm} \ne \hspace{0.09cm}1 - |H_1(f)| .$$ | + | *With no effect on the solution of the problem, note that this equation is not applicable for $τ ≠ 0$ because of: |
| + | :$$|H_{\rm HP}(f)|\hspace{0.09cm} \ne \hspace{0.09cm}1 - |H_1(f)| .$$ | ||
| − | |||
| − | === | + | |
| + | |||
| + | |||
| + | |||
| + | ''Please note:'' | ||
| + | *The exercise belongs to the chapter [[Linear_and_Time_Invariant_Systems/Some_Low-Pass_Functions_in_Systems_Theory|Some Low-Pass Functions in Systems Theory]]. | ||
| + | *In particular, reference is made to the page [[Linear_and_Time_Invariant_Systems/Some_Low-Pass_Functions_in_Systems_Theory#Slit_low-pass_filter_–_Rectangular-in-time|Slit low-pass filter]]. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Calculate the height $k$ of the impulse response $h_1(t)$ on the side condition of $H_1(f = 0) = 1$. |
|type="{}"} | |type="{}"} | ||
| − | $k =$ { 500 } 1/s | + | $k \ =\ $ { 500 3% } $\ \rm 1/s$ |
| − | { | + | {Let the input signal $x(t)$ be a rectangle symmetric about $t = 0$ of duration $T = 2 \ \rm ms$ and height $1 \, \rm V$. Let $τ = 0$ hold. <br>Which statements are true? |
|type="[]"} | |type="[]"} | ||
| − | - $y(t)$ | + | - $y(t)$ is rectangular. |
| − | + $y(t)$ | + | + $y(t)$ is triangular. |
| − | - $y(t)$ | + | - $y(t)$ is trapezoidal. |
| − | + | + | + The maximum value of $y(t)$ is $ 1\hspace{0.05cm} \rm V$. |
| − | { | + | {Which statements are true, if $x(t)$ has a rectangle width of $T = 1 \ \rm ms$ ? |
|type="[]"} | |type="[]"} | ||
| − | - $y(t)$ | + | - $y(t)$ is rectangular. |
| − | - $y(t)$ | + | - $y(t)$ is triangular. |
| − | + $y(t)$ | + | + $y(t)$ is trapezoidal. |
| − | - | + | - The maximum value of $y(t)$ is $1\hspace{0.05cm} \rm V$. |
| − | { | + | {The following still holds: $τ = 0$. Compute the output signal $z(t)$, if $x(t)$ jumps from zero to $1\hspace{0.05cm} \rm V$ at time $t = 0$ . <br>Which statements are true? |
|type="[]"} | |type="[]"} | ||
| − | - $z(t)$ | + | - $z(t)$ is an even function of time. |
| − | + $z(t)$ | + | + $z(t)$ has a jump discontinuity at $t = 0$ . |
| − | + | + | + At time $t = 0$ , $z(t) = 0$ holds. |
| − | + | + | + For $t > 1 \ \rm ms$ , $z(t) = 0$ is true. |
| − | { | + | {What is the curve shape of $z(t)$ in response to the step-shaped input signal $x(t)$, if the runtime is $τ =1 \hspace{0.05cm} \rm ms$ ? <br>What signal value occurs at $t =1 \hspace{0.05cm} \rm ms$ ? |
|type="{}"} | |type="{}"} | ||
| − | $z(t = 1 \rm \ ms) =$ { 0.5 } V | + | $z(t = 1 \rm \ ms) =\ $ { 0.5 3% } $\ \rm V$ |
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''1 | + | '''(1)''' The condition $H(f = 0) = 1$ means that the area of the impulse response is equal to $1$ . From this it follows that: |
| − | $$k = | + | :$$k = {1}/{\Delta t} \hspace{0.15cm}\underline{= 500\hspace{0.1cm}{ 1/{\rm s}}} .$$ |
| − | |||
| − | |||
| − | |||
| − | |||
| + | '''(2)''' <u>Approaches 2 and 4</u> are correct: | ||
| + | *The output signal $y(t)$ is obtained as the convolution product of $x(t)$ and $h(t)$. | ||
| + | *Convolution of two rectangles of equal width results in a triangle with its maximum at $t = 0$: | ||
| + | :$$y(t = 0 ) = 1\hspace{0.05cm}{\rm V}\cdot \int_{ - 1\,{\rm ms} }^{ 1\,{\rm ms} } {k \hspace{0.1cm}}{\rm d}\tau = | ||
| + | 1\hspace{0.05cm}{\rm V}\cdot \int_{ - 1\,{\rm ms} }^{ 1\,{\rm ms} } {\frac{1}{2\,{\rm ms}} \hspace{0.1cm}}{\rm d}\tau= 1\hspace{0.05cm}{\rm V}.$$ | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | [[File: P_ID859__LZI_A_1_6_c.png | right| frame|Trapezoid pulse]] | |
| − | + | '''(3)''' <u>Approach 3</u> is correct: | |
| − | + | *Convolution of two rectangles of different widths results in the trapezoidal output signal as shown in the sketch. | |
| − | + | *The maximum value occurs in the constant range from $-0.5 \hspace{0.05cm} \rm ms$ to $+0.5 \hspace{0.05cm} \rm ms$ and is | |
| − | + | :$$y(t = 0 ) = 1\hspace{0.05cm}{\rm V} \cdot \frac{1}{2\,{\rm | |
| − | + | ms}} \hspace{0.05cm}\cdot 1\,{\rm ms} = 0.5\hspace{0.05cm}{\rm V}.$$ | |
| − | |||
| − | ''' | + | [[File: P_ID860__LZI_A_1_6_d.png | right| frame|Non-causal HP step response]] |
| + | '''(4)''' <u>Approaches 2, 3 and 4</u> are correct: | ||
| + | *The impulse response of the total system is: $h_{\rm HP}(t) = \delta(t) - h(t).$ Both parts are shown in the sketch. | ||
| + | *The searched-for signal $z(t)$ is obtained via integration over $h_{\rm HP}(t)$ and multiplication by $1 \hspace{0.05cm} \rm V$ . <br>In the below sketch are shown: | ||
| + | :#the integral over $δ(t)$ blue, | ||
| + | :#the function $-σ(t)$ red, and | ||
| + | :#the entire signal $z(t)$ green. | ||
| + | *$z(t)$ is an odd function in $t$ with a jump discontinuity at $t = 0$: The signal value at $t = 0$ is exactly halfway between the left– and the right-hand limit and is therefore zero. | ||
| + | *For $t > 1 \hspace{0.05cm} \rm ms$ , $z(t) = 0$ holds, too, since the overall system has a high-pass characteristic. | ||
| + | <br clear=all> | ||
| + | [[File: P_ID861__LZI_A_1_6_e.png | right| frame|Causal HP step response]] | ||
| + | '''(5)''' The bottom graph shows the resulting impulse response $h_{\rm HP}(t)$ and the step response $σ_{\rm HP}(t)$. | ||
| + | *The latter jumps at $t = 0$ to the value $1$ and decays to the final value of "zero" until time $t = 2 \hspace{0.05cm} \rm ms$ . | ||
| + | *At time $t = 1\ \rm ms$ , the following is obtained: $σ_{\rm HP}(t) = 0.5$. | ||
| − | + | *The signal $z(t)$ is identical in shape to the step response $σ_{\rm HP}(t)$ but is yet to be multiplied by $1 \hspace{0.05cm} \rm V$ . | |
| + | *The searched-for signal value at time $t_1 = 1 \hspace{0.05cm} \rm ms$ thus results in $z(t_1) \; \rm \underline{ = \ 0.5 \: {\rm V}}$. | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| Line 93: | Line 118: | ||
| − | [[Category: | + | [[Category:Linear and Time-Invariant Systems: Exercises|^1.3 Some Low-Pass Functions in Systems Theory^]] |
Latest revision as of 14:49, 8 September 2021
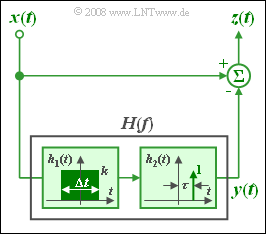
We consider below the constellation shown in the graph:
- The frequency response $H(f) = H_1(f) · H_2(f)$ in the lower branch is determined by the impulse responses of its two subcomponents.
- Here, $h_1(t)$ is constantly equal to $k$ in the reange from $-1\ \rm ms$ to $+1\ \rm ms$ and zero outside.
- At the range limits, half the value is valid in each case.
- The time variable drawn in the figure is thus $Δt = 2 \ \rm ms$.
The impulse response of the second system function $H_2(f)$ is:
- $$h_2(t) = \delta(t - \tau).$$
The frequency response between the signals $x(t)$ and $z(t)$ is of high-pass character and generally:
- $$H_{\rm HP}(f) = 1 - H_1(f) \cdot {\rm e}^{-{\rm j\hspace{0.05cm}\cdot \hspace{0.05cm}2 \pi}f \tau}.$$
- For the subtasks (1) to (4) the following holds: $τ = 0$ ⇒ $H(f) = H_1(f)$.
- However, using $τ = 0$ this can also be formulated as follows $(Δt = 2 \ \rm ms)$:
- $$H_{\rm HP}(f) = 1 - {\rm si}( \pi \cdot {\rm \Delta}t \cdot f).$$
- With no effect on the solution of the problem, note that this equation is not applicable for $τ ≠ 0$ because of:
- $$|H_{\rm HP}(f)|\hspace{0.09cm} \ne \hspace{0.09cm}1 - |H_1(f)| .$$
Please note:
- The exercise belongs to the chapter Some Low-Pass Functions in Systems Theory.
- In particular, reference is made to the page Slit low-pass filter.
Questions
Solution
(1) The condition $H(f = 0) = 1$ means that the area of the impulse response is equal to $1$ . From this it follows that:
- $$k = {1}/{\Delta t} \hspace{0.15cm}\underline{= 500\hspace{0.1cm}{ 1/{\rm s}}} .$$
(2) Approaches 2 and 4 are correct:
- The output signal $y(t)$ is obtained as the convolution product of $x(t)$ and $h(t)$.
- Convolution of two rectangles of equal width results in a triangle with its maximum at $t = 0$:
- $$y(t = 0 ) = 1\hspace{0.05cm}{\rm V}\cdot \int_{ - 1\,{\rm ms} }^{ 1\,{\rm ms} } {k \hspace{0.1cm}}{\rm d}\tau = 1\hspace{0.05cm}{\rm V}\cdot \int_{ - 1\,{\rm ms} }^{ 1\,{\rm ms} } {\frac{1}{2\,{\rm ms}} \hspace{0.1cm}}{\rm d}\tau= 1\hspace{0.05cm}{\rm V}.$$
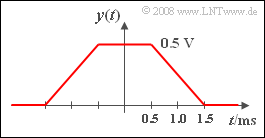
(3) Approach 3 is correct:
- Convolution of two rectangles of different widths results in the trapezoidal output signal as shown in the sketch.
- The maximum value occurs in the constant range from $-0.5 \hspace{0.05cm} \rm ms$ to $+0.5 \hspace{0.05cm} \rm ms$ and is
- $$y(t = 0 ) = 1\hspace{0.05cm}{\rm V} \cdot \frac{1}{2\,{\rm ms}} \hspace{0.05cm}\cdot 1\,{\rm ms} = 0.5\hspace{0.05cm}{\rm V}.$$
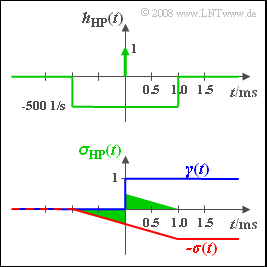
(4) Approaches 2, 3 and 4 are correct:
- The impulse response of the total system is: $h_{\rm HP}(t) = \delta(t) - h(t).$ Both parts are shown in the sketch.
- The searched-for signal $z(t)$ is obtained via integration over $h_{\rm HP}(t)$ and multiplication by $1 \hspace{0.05cm} \rm V$ .
In the below sketch are shown:
- the integral over $δ(t)$ blue,
- the function $-σ(t)$ red, and
- the entire signal $z(t)$ green.
- $z(t)$ is an odd function in $t$ with a jump discontinuity at $t = 0$: The signal value at $t = 0$ is exactly halfway between the left– and the right-hand limit and is therefore zero.
- For $t > 1 \hspace{0.05cm} \rm ms$ , $z(t) = 0$ holds, too, since the overall system has a high-pass characteristic.
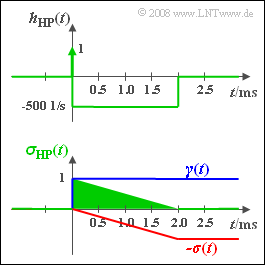
(5) The bottom graph shows the resulting impulse response $h_{\rm HP}(t)$ and the step response $σ_{\rm HP}(t)$.
- The latter jumps at $t = 0$ to the value $1$ and decays to the final value of "zero" until time $t = 2 \hspace{0.05cm} \rm ms$ .
- At time $t = 1\ \rm ms$ , the following is obtained: $σ_{\rm HP}(t) = 0.5$.
- The signal $z(t)$ is identical in shape to the step response $σ_{\rm HP}(t)$ but is yet to be multiplied by $1 \hspace{0.05cm} \rm V$ .
- The searched-for signal value at time $t_1 = 1 \hspace{0.05cm} \rm ms$ thus results in $z(t_1) \; \rm \underline{ = \ 0.5 \: {\rm V}}$.