Exercise 1.8Z: Cosine-Square Low-Pass Filter
When studying digital systems a dirac-shaped input signal $x(t) = T \cdot \delta(t)$ is often assumed such that $X(f) = T$ holds.
The output spectrum $Y(f)$ is then of equal form compared with the overall frequency response of the transmitter and receiver filter:
- $$H(f) = H_{\rm S}(f) \cdot H_{\rm E}(f).$$
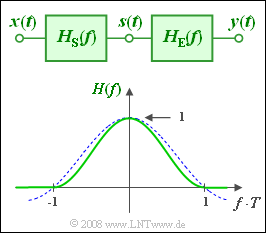
This frequency response is often assumed to be $\cos^2$-shaped (see graph):
- For $f \cdot T \ge 1$ , $H(f) = 0$ holds.
- In the inner region the following holds: $H(f) = \cos^2(f \cdot T \cdot {\pi}/{ 2} ) .$
Note that the equivalent bandwidth is $\Delta f = 1/{\Delta t}$ . Thus, for the equivalent ${\Delta t}$ of the impulse response one also obtains $T$ and the following holds:
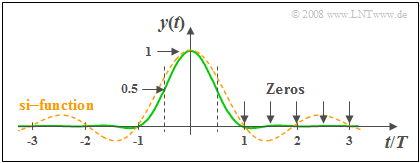
- $$y(t) = T \cdot h(t) = {\rm si}(\pi \cdot {t}/{T} )\cdot \frac {\cos(\pi \cdot t / T )}{1 - (2 \cdot t/T )^2}.$$
Also, note that the output signal $y(t)$ is dimensionless in cotrast to the impulse response $h(t)$ . This signal can also be represented as follows by applying trigonomic transformations:
- $$y(t) = {\pi}/{4} \cdot {\rm si}(\pi \cdot {t}/{T} )\cdot \big[ {\rm si}\big(\pi \cdot \left({t}/{T}+ 0.5 \right) \big)+ {\rm si}\big(\pi \cdot \left({t}/{T}- 0.5 \right) \big)\big].$$
For each of the following tasks select the equation that is easier to handle.
For subtask (3) it shall be assumed that the signal $s(t)$ is a rectangular pulse in the middle between the two frequency responses $H_{\rm S}(f)$ and $H_{\rm S}(f)$ . Consequently, it must hold:
- $$H_{\rm E}(f) = {\rm si }(\pi f T ) .$$
Please note:
- The exercise belongs to the chapter Some Low-Pass Functions in Systems Theory.
- In particular, reference is made to the page Cosine–square low-pass filter.
- You can check your results with the interactive applet Frequency response and impulse response.
Questions
Solution
- From the second equation these results are obtained, for example
- $$y(t = 0) = {\pi}/{4} \cdot {\rm si}(0)\cdot \left[ {\rm si}(\pi/2)+ {\rm si}(-\pi/2)\right] {\pi}/{2} \cdot {\rm si}(\pi/2) = {\pi}/{2} \cdot \frac{{\rm sin}(\pi/2)}{\pi/2} \hspace{0.15cm}\underline{= 1},$$
- $$y(t = T) \hspace{0.15cm}=\hspace{0.15cm}{\pi}/{4} \cdot {\rm si}(\pi)\cdot \left[ {\rm si}(3\pi/2)+ {\rm si}(\pi/2)\right] \hspace{0.15cm}\underline{= 0}.$$
(2) The second representation is more suitable for the computation of these signal values:
- $$y(t = T/2) = {\pi}/{4} \cdot {\rm si}(\pi/2)\cdot \big[ {\rm si}(\pi)+ {\rm si}(0)\big].$$
- Considering ${\rm si}(0) = 1$ and ${\rm si}(\pi) = 0$ one obtains thus:
- $$y(t = T/2) = {\pi}/{4} \cdot {\rm si}(\pi/2)= {\pi}/{4} \cdot \frac{{\rm sin}(\pi/2)}{\pi/2} \hspace{0.15cm}\underline{ = 0.5}.$$
- Analogously, the following is obtained for $t = 1.5T$:
- $$y(t = 1.5T) = {\pi}/{4} \cdot {\rm si}(3\pi/2)\cdot \left[ {\rm si}(2\pi)+ {\rm si}(\pi)\right] \hspace{0.15cm}\underline{ = 0}.$$
- Here, ${\rm si}(\pi) = {\rm si}(2\pi) = 0$ is considered.
- Also, at times $t/T = 2.5, 3.5,\text{ ... }$ , $y(t) = 0$ holds as shown in the above graph.
(3) For large values of $t$ the following holds by approximation (neglecting the "1" in the denominator):
- $$y(t)= {\rm si}(\pi \cdot {t}/{T} )\cdot \frac {\cos(\pi \cdot t / T )}{1 - (2 \cdot t/T )^2} \approx \frac {\sin(\pi \cdot t / T )\cdot \cos(\pi \cdot t / T )}{ - (\pi \cdot t/T )(2 \cdot t/T )^2} = - \frac {\sin(2\pi \cdot t / T )}{ 8 \pi \cdot( t/T )^3}.$$
- This takes into account that $\sin(\alpha) \cdot \cos(\alpha) = \sin(2\alpha)/2$ .
- Hence at time $t = 10.75 T$ it holds that:
- $$\sin(2\pi \cdot t / T ) = \sin (21.5\pi)= \sin (1.5\pi) = -1\hspace{0.3cm} \Rightarrow \hspace{0.3cm} y(t = 10.75 T) = \frac {1 }{ 8 \pi \cdot( 10.75 )^3} \hspace{0.15cm}\underline{= 32 \cdot 10^{-6}}.$$
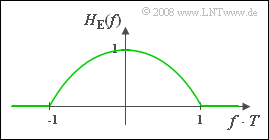
(4) The receiver frequency response is the following for $|f \cdot T| \le 1$:
- $$H_{\rm E}(f) = \frac{H(f)}{H_{\rm S}(f)}= \frac{\cos^2(\pi f T /2)}{{\rm si}(\pi fT)}.$$
- This function curve is shown in the graph. The following holds or the interpolation values:
- $$H_{\rm E}(f = 0) = \frac{\cos^2(0)}{{\rm si}(0)} \hspace{0.15cm}\underline{ = 1},$$
- $$H_{\rm E}(f = {0.5}/T \hspace{-0.15cm} = \hspace{-0.15cm} \frac{\cos^2(\pi/4)}{{\rm si}(\pi/2)}= (\sqrt{2} / 2)^2 \cdot \frac{\pi}{2} = \hspace{-0.15cm} \frac{\pi}{4}\hspace{0.15cm}\underline{ \approx 0.785},$$
- $$H_{\rm E}(f = {1}/{T}) = \frac{\cos^2(\pi/2)}{{\rm si}(\pi)} = "0/0"\hspace{0.15cm}\underline{= 0}.$$
This result takes into account that in the whole frequency domain $H_{\rm S}(f) \ge H(f) $ holds. Actually, the last calculated value should be determined by a limiting process in a mathematically exact way. We did that too, but not in this sample solution.