Difference between revisions of "Aufgaben:Exercise 2.08: Generator Polynomials for Reed-Solomon"
From LNTwww
| (31 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Channel_Coding/Definition_and_Properties_of_Reed-Solomon_Codes}} |
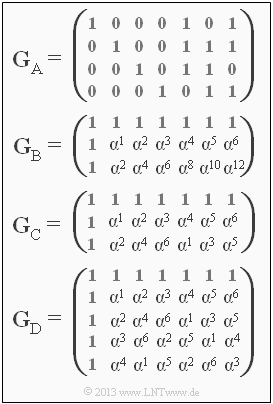
| − | [[File:P_ID2525__KC_A_2_8.png|right|frame| | + | [[File:P_ID2525__KC_A_2_8.png|right|frame|Four generator matrices, three of which describe Reed-Solomon codes]] |
| − | In | + | In the [[Aufgaben:Exercise_2.07:_Reed-Solomon_Code_(7,_3,_5)_to_Base_8|"Exercise 2.7"]] you should determine the code words of the $\rm RSC \, (7, \, 3, \, 5)_8$ via a polynomial. However, you can also determine the code word $\underline{c}$ from the information word $\underline{u}$ and the generator matrix $\mathbf{G}$ according to the following equation: |
:$$\underline {c} = \underline {u} \cdot { \boldsymbol{\rm G}} | :$$\underline {c} = \underline {u} \cdot { \boldsymbol{\rm G}} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | *Two of these generator matrices describe the $\rm RSC \, (7, \, 3, \, 5)_8$. In the subtask '''(1)''' is explicitly asked which. | |
| + | |||
| + | *Another generator matrix belongs to $\rm RSC \, (7, \, 5, \, 3)_8$, which is considered in subtask '''(3)'''. | ||
| − | |||
| − | |||
| − | |||
| + | Hints: | ||
| + | * This exercise belongs to the chapter [[Channel_Coding/Definition_and_Properties_of_Reed-Solomon_Codes| "Definition and Properties of Reed-Solomon Codes"]]. | ||
| − | === | + | * Important information about Reed–Solomon codes can also be found in [[Aufgaben:Exercise_2.07:_Reed-Solomon_Code_(7,_3,_5)_to_Base_8| "Exercise 2.7"]]. |
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Which of the generator polynomials describe the $\rm RSC \, (7, \, 3, \, 5)_8$? |
|type="[]"} | |type="[]"} | ||
| − | - $\mathbf{G}_{\rm A}$, | + | - the matrix $\mathbf{G}_{\rm A}$, |
| − | + $\mathbf{G}_{\rm B}$, | + | + the matrix $\mathbf{G}_{\rm B}$, |
| − | + $\mathbf{G}_{\rm C}$, | + | + the matrix $\mathbf{G}_{\rm C}$, |
| − | - $\mathbf{G}_{\rm D}$. | + | - the matrix $\mathbf{G}_{\rm D}$. |
| − | { | + | {The information sequence starts with $\alpha^4, \, 1, \, \alpha^3, \, 0, \, \alpha^6$. Determine the first code word for the $\rm RSC \, (7, \, 3, \, 5)_8$. |
|type="[]"} | |type="[]"} | ||
| − | + | + | + It holds $c_0 = \alpha^2$, |
| − | + | + | + It holds $c_1 = \alpha^3$, |
| − | - | + | - It holds $c_6 = 0$. |
| − | { | + | {What is the code word for the $\rm RSC \, (7, \, 5, \, 3)_8$ given the same sequence of information? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + It holds $c_0 = 1$, |
| − | + | + | + It holds $c_1 = 0$, |
| − | + | + | + It holds $c_6 = \alpha^6$. |
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' Correct are the <u>solutions 2 and 3</u> ⇒ matrices $\mathbf{G}_{\rm B}$ and $\mathbf{G}_{\rm C}$. |
| + | *In the matrix $\mathbf{G}_{\rm C}$ the allowed transformations $\alpha^8 = \alpha, \ \alpha^{10} = \alpha^3$ and $\alpha^{12} = \alpha^5$ have already been considered. | ||
| + | |||
| + | *The matrix $\mathbf{G}_{\rm A}$ holds for the $(7, \, 5, \, 3)$ Hamming code and $\mathbf{G}_{\rm D}$ belongs to the $\rm RSC \, (7, \, 5, \, 3)_8$. See subtask '''(3)''' for more details. | ||
| + | |||
| − | '''(2)''' | + | '''(2)''' In the $\rm RSC \, (7, \, 3, \, 5)_8$, in each coding step are processed $k = 3$ information symbols, <br>in coding step 1 according to the specification the symbols $\alpha^4, \ 1$ and $\alpha^3$. |
| + | |||
| + | *With the generator matrix $\mathbf{G}_{\rm C}$ thus holds: | ||
:$$\underline {c} = \underline {u} \cdot { \boldsymbol{\rm G}}_{\rm C} = | :$$\underline {c} = \underline {u} \cdot { \boldsymbol{\rm G}}_{\rm C} = | ||
\begin{pmatrix} | \begin{pmatrix} | ||
| Line 53: | Line 66: | ||
1 & \alpha^2 & \alpha^4 & \alpha^6 & \alpha^1 & \alpha^{3} & \alpha^{5} | 1 & \alpha^2 & \alpha^4 & \alpha^6 & \alpha^1 & \alpha^{3} & \alpha^{5} | ||
\end{pmatrix}\hspace{0.05cm}. $$ | \end{pmatrix}\hspace{0.05cm}. $$ | ||
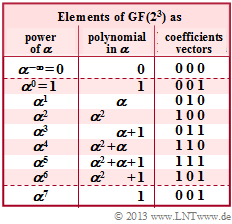
| − | + | [[File:EN_KC_Z_2_5_neu.png|right|frame|$\rm GF(2^3)$ representation as powers, polynomials, vectors]] | |
| − | [[File: | + | |
| − | :$$c_0 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha^{4}\cdot 1 + 1 \cdot 1 + \alpha^{3}\cdot 1 = | + | *This results according to the adjacent auxiliary table: |
| − | + | :$$c_0 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha^{4}\cdot 1 + 1 \cdot 1 + \alpha^{3}\cdot 1 = | |
(110) + (001) + (011)= (100) = \alpha^{2} \hspace{0.05cm},$$ | (110) + (001) + (011)= (100) = \alpha^{2} \hspace{0.05cm},$$ | ||
| − | :$$c_1 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha^{4}\cdot 1 + 1 \cdot \alpha + \alpha^{3}\cdot \alpha^{2}= | + | :$$c_1 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha^{4}\cdot 1 + 1 \cdot \alpha + \alpha^{3}\cdot \alpha^{2}= |
| − | |||
(110) + (010) + (110) = (011) = \alpha^{3} \hspace{0.05cm},$$ | (110) + (010) + (110) = (011) = \alpha^{3} \hspace{0.05cm},$$ | ||
| − | :$$c_2 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha^{4}\cdot 1 + 1 \cdot \alpha^{2} + \alpha^{3}\cdot \alpha^{4}= | + | :$$c_2 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha^{4}\cdot 1 + 1 \cdot \alpha^{2} + \alpha^{3}\cdot \alpha^{4}= |
| − | |||
(110) + (100) + (001) = (011) = \alpha^{3} \hspace{0.05cm},$$ | (110) + (100) + (001) = (011) = \alpha^{3} \hspace{0.05cm},$$ | ||
| − | :$$c_3 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha^{4}\cdot 1 + 1 \cdot \alpha^{3} + \alpha^{3}\cdot \alpha^{6}=$ | + | :$$c_3 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha^{4}\cdot 1 + 1 \cdot \alpha^{3} + \alpha^{3}\cdot \alpha^{6}=$ |
| − | |||
(110) + (011) + (100) = (001) = 1 \hspace{0.05cm},$$ | (110) + (011) + (100) = (001) = 1 \hspace{0.05cm},$$ | ||
:$$c_4 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha^{4}\cdot 1 + 1 \cdot \alpha^{4} + \alpha^{3}\cdot \alpha^{1} | :$$c_4 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha^{4}\cdot 1 + 1 \cdot \alpha^{4} + \alpha^{3}\cdot \alpha^{1} | ||
= \alpha^{4} \hspace{0.05cm},$$ | = \alpha^{4} \hspace{0.05cm},$$ | ||
| − | :$$c_5 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha^{4}\cdot 1 + 1 \cdot \alpha^{5} + \alpha^{3}\cdot \alpha^{3}= | + | :$$c_5 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha^{4}\cdot 1 + 1 \cdot \alpha^{5} + \alpha^{3}\cdot \alpha^{3}= |
| − | |||
(110) + (111) + (101) = (100) = \alpha^{2} \hspace{0.05cm},$$ | (110) + (111) + (101) = (100) = \alpha^{2} \hspace{0.05cm},$$ | ||
| − | :$$c_6 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha^{4}\cdot 1 + 1 \cdot \alpha^{6} + \alpha^{3}\cdot \alpha^{5}= | + | :$$c_6 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha^{4}\cdot 1 + 1 \cdot \alpha^{6} + \alpha^{3}\cdot \alpha^{5}= |
| − | |||
(\alpha^{2} + \alpha) + (\alpha^2 +1) + \alpha = 1 \hspace{0.05cm}.$$ | (\alpha^{2} + \alpha) + (\alpha^2 +1) + \alpha = 1 \hspace{0.05cm}.$$ | ||
| − | + | *You get exactly the same result as in subtask '''(4)''' of [[Aufgaben:Exercise_2.07:_Reed-Solomon_Code_(7,_3,_5)_to_Base_8|"Exercise 2.7"]]. Correct are the <u>solutions 1 and 2</u>. | |
| + | *So it is not $c_6 = 0$, but $c_6 = 1$. | ||
| − | '''(3)''' | + | |
| + | '''(3)''' At the $\rm RSC \, (7, \, 5, \, 3)_8$, the information word $\underline{u} = (u_0, \, u_1, \, u_2, \, u_3, \, u_4)$ must be considered. | ||
| + | *With the generator matrix $\mathbf{G}_{\rm D}$ one obtains: | ||
:$$\underline {c} = \underline {u} \cdot { \boldsymbol{\rm G}}_{\rm D} = | :$$\underline {c} = \underline {u} \cdot { \boldsymbol{\rm G}}_{\rm D} = | ||
\begin{pmatrix} | \begin{pmatrix} | ||
| Line 92: | Line 103: | ||
\end{pmatrix}\hspace{0.05cm}. $$ | \end{pmatrix}\hspace{0.05cm}. $$ | ||
| − | + | *From this it follows: | |
| − | :$$c_0 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha^{4}\cdot 1 + 1 \cdot 1 + \alpha^{3}\cdot 1 + 0 \cdot 1 + \alpha^{6}\cdot 1= | + | :$$c_0 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha^{4}\cdot 1 + 1 \cdot 1 + \alpha^{3}\cdot 1 + 0 \cdot 1 + \alpha^{6}\cdot 1= (110) + (001) + (011) + (000) + (101) = (001) = 1 \hspace{0.05cm},$$ |
| − | |||
:$$c_1 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \left [ \alpha^{4}\cdot 1 + 1 \cdot \alpha + \alpha^{3}\cdot \alpha^{2} \right ] + 0 \cdot \alpha^{3} + \alpha^{6}\cdot \alpha^{4}= \left [ \alpha^{3} \right ] + \alpha^{3} = 0 \hspace{0.05cm}.$$ | :$$c_1 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \left [ \alpha^{4}\cdot 1 + 1 \cdot \alpha + \alpha^{3}\cdot \alpha^{2} \right ] + 0 \cdot \alpha^{3} + \alpha^{6}\cdot \alpha^{4}= \left [ \alpha^{3} \right ] + \alpha^{3} = 0 \hspace{0.05cm}.$$ | ||
| − | + | *This takes into account that the bracket expression $[ \ \text{...} \ ]$ corresponds exactly to the result $c_1$ of subtask '''(2)'''. | |
| + | |||
| + | *Corresponding is also considered in the following calculations: | ||
:$$c_2 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \left [ \alpha^{3} \right ] + \alpha^{6}\cdot \alpha^{1}= | :$$c_2 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \left [ \alpha^{3} \right ] + \alpha^{6}\cdot \alpha^{1}= | ||
\left [ \alpha^{3} \right ] + \alpha^{7} = | \left [ \alpha^{3} \right ] + \alpha^{7} = | ||
| Line 113: | Line 125: | ||
= (001) + (100) = (101) = \alpha^{6} \hspace{0.05cm}.$$ | = (001) + (100) = (101) = \alpha^{6} \hspace{0.05cm}.$$ | ||
| − | + | *This means: <u>All proposed solutions</u> are correct. | |
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category: | + | [[Category:Channel Coding: Exercises|^2.3 Reed–Solomon Codes^]] |
Latest revision as of 16:11, 10 October 2022
In the "Exercise 2.7" you should determine the code words of the $\rm RSC \, (7, \, 3, \, 5)_8$ via a polynomial. However, you can also determine the code word $\underline{c}$ from the information word $\underline{u}$ and the generator matrix $\mathbf{G}$ according to the following equation:
- $$\underline {c} = \underline {u} \cdot { \boldsymbol{\rm G}} \hspace{0.05cm}.$$
- Two of these generator matrices describe the $\rm RSC \, (7, \, 3, \, 5)_8$. In the subtask (1) is explicitly asked which.
- Another generator matrix belongs to $\rm RSC \, (7, \, 5, \, 3)_8$, which is considered in subtask (3).
Hints:
- This exercise belongs to the chapter "Definition and Properties of Reed-Solomon Codes".
- Important information about Reed–Solomon codes can also be found in "Exercise 2.7".
Questions
Solution
(1) Correct are the solutions 2 and 3 ⇒ matrices $\mathbf{G}_{\rm B}$ and $\mathbf{G}_{\rm C}$.
- In the matrix $\mathbf{G}_{\rm C}$ the allowed transformations $\alpha^8 = \alpha, \ \alpha^{10} = \alpha^3$ and $\alpha^{12} = \alpha^5$ have already been considered.
- The matrix $\mathbf{G}_{\rm A}$ holds for the $(7, \, 5, \, 3)$ Hamming code and $\mathbf{G}_{\rm D}$ belongs to the $\rm RSC \, (7, \, 5, \, 3)_8$. See subtask (3) for more details.
(2) In the $\rm RSC \, (7, \, 3, \, 5)_8$, in each coding step are processed $k = 3$ information symbols,
in coding step 1 according to the specification the symbols $\alpha^4, \ 1$ and $\alpha^3$.
- With the generator matrix $\mathbf{G}_{\rm C}$ thus holds:
- $$\underline {c} = \underline {u} \cdot { \boldsymbol{\rm G}}_{\rm C} = \begin{pmatrix} \alpha^4 & 1 & \alpha^3 \end{pmatrix} \cdot \begin{pmatrix} 1 & 1 & 1 & 1 & 1 & 1 & 1\\ 1 & \alpha^1 & \alpha^2 & \alpha^3 & \alpha^4 & \alpha^5 & \alpha^6\\ 1 & \alpha^2 & \alpha^4 & \alpha^6 & \alpha^1 & \alpha^{3} & \alpha^{5} \end{pmatrix}\hspace{0.05cm}. $$
- This results according to the adjacent auxiliary table:
- $$c_0 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha^{4}\cdot 1 + 1 \cdot 1 + \alpha^{3}\cdot 1 = (110) + (001) + (011)= (100) = \alpha^{2} \hspace{0.05cm},$$
- $$c_1 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha^{4}\cdot 1 + 1 \cdot \alpha + \alpha^{3}\cdot \alpha^{2}= (110) + (010) + (110) = (011) = \alpha^{3} \hspace{0.05cm},$$
- $$c_2 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha^{4}\cdot 1 + 1 \cdot \alpha^{2} + \alpha^{3}\cdot \alpha^{4}= (110) + (100) + (001) = (011) = \alpha^{3} \hspace{0.05cm},$$
- $$c_3 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha^{4}\cdot 1 + 1 \cdot \alpha^{3} + \alpha^{3}\cdot \alpha^{6}=$ (110) + (011) + (100) = (001) = 1 \hspace{0.05cm},$$
- $$c_4 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha^{4}\cdot 1 + 1 \cdot \alpha^{4} + \alpha^{3}\cdot \alpha^{1} = \alpha^{4} \hspace{0.05cm},$$
- $$c_5 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha^{4}\cdot 1 + 1 \cdot \alpha^{5} + \alpha^{3}\cdot \alpha^{3}= (110) + (111) + (101) = (100) = \alpha^{2} \hspace{0.05cm},$$
- $$c_6 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha^{4}\cdot 1 + 1 \cdot \alpha^{6} + \alpha^{3}\cdot \alpha^{5}= (\alpha^{2} + \alpha) + (\alpha^2 +1) + \alpha = 1 \hspace{0.05cm}.$$
- You get exactly the same result as in subtask (4) of "Exercise 2.7". Correct are the solutions 1 and 2.
- So it is not $c_6 = 0$, but $c_6 = 1$.
(3) At the $\rm RSC \, (7, \, 5, \, 3)_8$, the information word $\underline{u} = (u_0, \, u_1, \, u_2, \, u_3, \, u_4)$ must be considered.
- With the generator matrix $\mathbf{G}_{\rm D}$ one obtains:
- $$\underline {c} = \underline {u} \cdot { \boldsymbol{\rm G}}_{\rm D} = \begin{pmatrix} \alpha^4 & 1 & \alpha^3 & 0 & \alpha^6 \end{pmatrix} \cdot \begin{pmatrix} 1 & 1 & 1 & 1 & 1 & 1 & 1\\ 1 & \alpha^1 & \alpha^2 & \alpha^3 & \alpha^4 & \alpha^5 & \alpha^6\\ 1 & \alpha^2 & \alpha^4 & \alpha^6 & \alpha^1 & \alpha^{3} & \alpha^{5}\\ 1 & \alpha^3 & \alpha^6 & \alpha^2 & \alpha^5 & \alpha^{1} & \alpha^{4}\\ 1 & \alpha^4 & \alpha^1 & \alpha^5 & \alpha^2 & \alpha^{6} & \alpha^{3} \end{pmatrix}\hspace{0.05cm}. $$
- From this it follows:
- $$c_0 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha^{4}\cdot 1 + 1 \cdot 1 + \alpha^{3}\cdot 1 + 0 \cdot 1 + \alpha^{6}\cdot 1= (110) + (001) + (011) + (000) + (101) = (001) = 1 \hspace{0.05cm},$$
- $$c_1 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \left [ \alpha^{4}\cdot 1 + 1 \cdot \alpha + \alpha^{3}\cdot \alpha^{2} \right ] + 0 \cdot \alpha^{3} + \alpha^{6}\cdot \alpha^{4}= \left [ \alpha^{3} \right ] + \alpha^{3} = 0 \hspace{0.05cm}.$$
- This takes into account that the bracket expression $[ \ \text{...} \ ]$ corresponds exactly to the result $c_1$ of subtask (2).
- Corresponding is also considered in the following calculations:
- $$c_2 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \left [ \alpha^{3} \right ] + \alpha^{6}\cdot \alpha^{1}= \left [ \alpha^{3} \right ] + \alpha^{7} = (011) + (001) = (010) = \alpha^{1} \hspace{0.05cm},$$
- $$c_3 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \left [ 1 \right ] + \alpha^{6}\cdot \alpha^{5}= \left [ 1 \right ] + \alpha^{4}= (001) + (110) = (111) = \alpha^{5} \hspace{0.05cm},$$
- $$c_4 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \left [ \alpha^{4} \right ] + \alpha^{6}\cdot \alpha^{2}= \left [ \alpha^{4} \right ] + \alpha^{1} = (110) + (010) = (100) = \alpha^{2} \hspace{0.05cm},$$
- $$c_5 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \left [ \alpha^{2} \right ] + \alpha^{6}\cdot \alpha^{6}= \left [ \alpha^{2} \right ] + \alpha^{5} = (100) + (111) = (011) = \alpha^{3} \hspace{0.05cm},$$
- $$c_6 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \left [ 1 \right ] + \alpha^{6}\cdot \alpha^{3}= \left [ 1 \right ] + \alpha^{2} = (001) + (100) = (101) = \alpha^{6} \hspace{0.05cm}.$$
- This means: All proposed solutions are correct.