Exercise 2.08Z: Addition and Multiplication in GF(2 power 3)
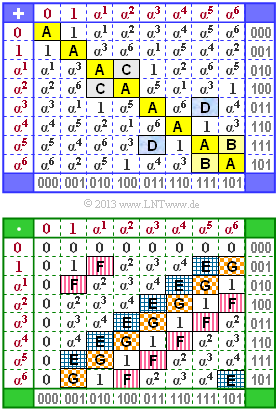
The graph shows the addition and multiplication table for the finite field $\rm GF(2^3)$. The tables are not complete. Some fields (highlighted in color) should be completed.
The elements are given both in the exponent representation (with red lettering, left and above) and in the coefficient representation (gray lettering, right and below). From this assignment one can already recognize the underlying irreducible polynomial $p(\alpha)$.
- Additions (and subtractions) are best done in the coefficient representation (or with the polynomials firmly linked to it).
- For multiplications, however, the exponent representation is more convenient.
Hints:
- Die Aufgabe gehört zum Kapitel "Definition and Properties of Reed-Solomon Codes".
- However, reference is also made to the chapter "Extension Field".
Questions
Solution
- $$\alpha^3 + \alpha^3 = (011) + (011) = (000) = 0 \hspace{0.05cm}.$$
That is: $\rm A$stands for the zero element ⇒ Solution 1.
(2) $\rm B$ is the result of adding $\alpha^5$ and $\alpha^6$ ⇒ Solution 3:
- $$\alpha^5 + \alpha^6 = (111) + (101) = (010) = \alpha^1 \hspace{0.05cm}.$$
- One could have found this result more simply, since in each row and column each element occurs exactly once.
- After $\rm A = 0$ is fixed, exactly only the element $\alpha^1$ is missing in the last row and the last column.
(3) $\rm C$ is the result of the sum of $\alpha^1$ and $\alpha^2$ ⇒ Solution 3:
- $$\alpha^1 + \alpha^2 = (010) + (100) = (110) = \alpha^4 \hspace{0.05cm}.$$
(4) $\rm D$ is the result of $\alpha^3$ and $\alpha^5$ ⇒ Solution 1:
- $$\alpha^3 + \alpha^5 = (011) + (111) = (100) = \alpha^2 \hspace{0.05cm}.$$
(5) All proposed solutions are correct, as can be seen from row 2 (multiplication with the identity element):
- The complete tables for addition and multiplication are shown opposite.
- Because of the validity of $\alpha^i \cdot \alpha^j = \alpha^{(i+j)\hspace{0.1cm} {\rm mod}\hspace{0.1cm} 7} $, multiplication yields a symmetry that could be used to solve.
(6) Correct here is the proposed solution 3:
- All polynomials are indeed irreducible. However, one needs a degree 3 polynomial for $\rm GF(2^3)$.
- The third proposed solution results from the relation
- $$\alpha^3 = \alpha + 1 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} p(\alpha) = \alpha^3 + \alpha + 1 = 0 \hspace{0.05cm}.$$