Difference between revisions of "Aufgaben:Exercise 2.13: Quadrature Amplitude Modulation"
m |
|||
| Line 3: | Line 3: | ||
}} | }} | ||
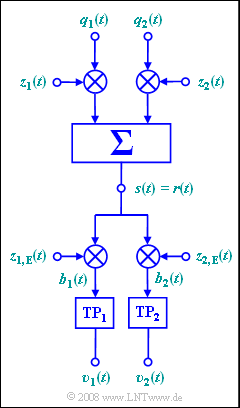
| − | [[File:P_ID1055__Mod_A_2_11.png|right|frame| | + | [[File:P_ID1055__Mod_A_2_11.png|right|frame| $\rm QAM$ model under consideration]] |
| − | + | The ''quadrature amplitude modulation'' $\rm (QAM)$ explained by the graph allows the transmission of two source signals $q_1(t)$ and $q_2(t)$ over the same channel, under certain boundary conditions, which are to be determined in this task. | |
| − | In | + | In this exercise, with $A_1 = A_2 = 2\ \rm V$, let: |
:$$q_1(t) = A_1 \cdot \cos(2 \pi \cdot f_{\rm 1} \cdot t),$$ | :$$q_1(t) = A_1 \cdot \cos(2 \pi \cdot f_{\rm 1} \cdot t),$$ | ||
:$$q_2(t) = A_2 \cdot \sin(2 \pi \cdot f_{\rm 2} \cdot t)\hspace{0.05cm}.$$ | :$$q_2(t) = A_2 \cdot \sin(2 \pi \cdot f_{\rm 2} \cdot t)\hspace{0.05cm}.$$ | ||
| − | + | For $ω_{\rm T} = 2π · 25\ \rm kHz$, the four carrier signals plotted in the graph are: | |
:$$z_1(t) = \cos(\omega_{\rm T} \cdot t),$$ | :$$z_1(t) = \cos(\omega_{\rm T} \cdot t),$$ | ||
:$$ z_2(t) = \sin(\omega_{\rm T} \cdot t),$$ | :$$ z_2(t) = \sin(\omega_{\rm T} \cdot t),$$ | ||
:$$ z_{1,\hspace{0.05cm}{\rm E}}(t) = 2 \cdot \cos(\omega_{\rm T} \cdot t + \Delta \phi_{\rm T}),$$ | :$$ z_{1,\hspace{0.05cm}{\rm E}}(t) = 2 \cdot \cos(\omega_{\rm T} \cdot t + \Delta \phi_{\rm T}),$$ | ||
:$$ z_{2,\hspace{0.05cm}{\rm E}}(t) = 2 \cdot \sin(\omega_{\rm T} \cdot t + \Delta \phi_{\rm T})\hspace{0.05cm}.$$ | :$$ z_{2,\hspace{0.05cm}{\rm E}}(t) = 2 \cdot \sin(\omega_{\rm T} \cdot t + \Delta \phi_{\rm T})\hspace{0.05cm}.$$ | ||
| − | + | Both lowpass filters $\rm TP_1$ and $\rm TP_2$ with input signals $b_1(t)$ and $b_2(t)$ , respectively, remove all frequency components $|f| > f_{\rm T}$. | |
| Line 22: | Line 22: | ||
| − | '' | + | ''Hints:'' |
| − | * | + | *This exercise belongs to the chapter [[Modulation_Methods/Further_AM_Variants|Further AM Variants]]. |
| − | * | + | *Particular reference is made to the page [[Modulation_Methods/#Quadrature_Amplitude_Modulation_.28QAM.29|Quadrature Amplitude Modulation (QAM)]]. |
| − | * | + | *It is worth noting that the carrier signals $z_2(t)$ and $z_{2,\hspace{0.05cm}{\rm E}}(t)$ are applied with positive signs here. |
| − | * | + | *Often – as in the theory section – these carrier signals are given as "minus-sine". |
| − | * | + | *The following trigonometric transformations are given: |
:$$ \cos(\alpha) \cdot \cos(\beta) = 1/2 \cdot \big[ \cos(\alpha - \beta)+ \cos(\alpha + \beta) \big],$$ | :$$ \cos(\alpha) \cdot \cos(\beta) = 1/2 \cdot \big[ \cos(\alpha - \beta)+ \cos(\alpha + \beta) \big],$$ | ||
:$$ \sin(\alpha) \cdot \sin(\beta) = 1/2 \cdot \big[ \cos(\alpha - \beta)- \cos(\alpha + \beta) \big],$$ | :$$ \sin(\alpha) \cdot \sin(\beta) = 1/2 \cdot \big[ \cos(\alpha - \beta)- \cos(\alpha + \beta) \big],$$ | ||
| Line 35: | Line 35: | ||
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Calculate the transmitted signal $s(t)$ in the case that $f_1 ≠ f_2$. Which of the following statements apply?|type="()"} |
| − | |type="()"} | + | - $s(t)$ is composed of two cosine and two sine oscillations. |
| − | - $s(t)$ | + | + $s(t)$ is composed of four cosine oscillations. |
| − | + $s(t)$ | + | - $s(t)$ is composed of four sine oscillations. |
| − | - $s(t)$ | ||
| − | { | + | {What is $s(t)$ when $f_1 = f_2 = 5 \ \rm kHz$. What signal value arises for $t = 50 \ \rm µ s$ ? |
|type="{}"} | |type="{}"} | ||
$s(t = 50 \ \rm µ s) \ = \ $ { 2 3% } $\ \rm V$ | $s(t = 50 \ \rm µ s) \ = \ $ { 2 3% } $\ \rm V$ | ||
| − | { | + | {Calculate the sink signals $v_1(t)$ and $v_2(t)$ for $f_1 = f_2$ and $Δϕ_{\rm T} = 0$ (no phase offset). Which statements are true? |
|type="()"} | |type="()"} | ||
| − | + | + | + $v_1(t) = q_1(t)$ and $v_2(t) = q_2(t)$ both hold. |
| − | - | + | - Linear distortions occur. |
| − | - | + | - Nonlinear distortions occur. |
| − | { | + | {Calculate the sink signals $v_1(t)$ and $v_2(t)$ for $f_1 = f_2$ and a phase offset $Δϕ_{\rm T} = 30^\circ$. Which statements are true? |
|type="()"} | |type="()"} | ||
| − | - | + | - $v_1(t) = q_1(t)$ and $v_2(t) = q_2(t)$ both hold. |
| − | + | + | + Linear distortions occur. |
| − | - | + | - Nonlinear distortions occur. |
| − | { | + | {Which of the following statements apply when $f_1 ≠ f_2$ and $Δϕ_{\rm T} ≠ 0$ (with an arbitrary phase offset)? |
|type="[]"} | |type="[]"} | ||
| − | - | + | - $v_1(t) = q_1(t)$ and $v_2(t) = q_2(t)$ both hold. |
| − | - | + | - Linear distortions occur. |
| − | + | + | + Nonlinear distortions occur. |
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
'''(1)''' Mit den angegebenen trigonometrischen Umformungen erhält man: | '''(1)''' Mit den angegebenen trigonometrischen Umformungen erhält man: | ||
Revision as of 18:11, 23 December 2021
The quadrature amplitude modulation $\rm (QAM)$ explained by the graph allows the transmission of two source signals $q_1(t)$ and $q_2(t)$ over the same channel, under certain boundary conditions, which are to be determined in this task.
In this exercise, with $A_1 = A_2 = 2\ \rm V$, let:
- $$q_1(t) = A_1 \cdot \cos(2 \pi \cdot f_{\rm 1} \cdot t),$$
- $$q_2(t) = A_2 \cdot \sin(2 \pi \cdot f_{\rm 2} \cdot t)\hspace{0.05cm}.$$
For $ω_{\rm T} = 2π · 25\ \rm kHz$, the four carrier signals plotted in the graph are:
- $$z_1(t) = \cos(\omega_{\rm T} \cdot t),$$
- $$ z_2(t) = \sin(\omega_{\rm T} \cdot t),$$
- $$ z_{1,\hspace{0.05cm}{\rm E}}(t) = 2 \cdot \cos(\omega_{\rm T} \cdot t + \Delta \phi_{\rm T}),$$
- $$ z_{2,\hspace{0.05cm}{\rm E}}(t) = 2 \cdot \sin(\omega_{\rm T} \cdot t + \Delta \phi_{\rm T})\hspace{0.05cm}.$$
Both lowpass filters $\rm TP_1$ and $\rm TP_2$ with input signals $b_1(t)$ and $b_2(t)$ , respectively, remove all frequency components $|f| > f_{\rm T}$.
Hints:
- This exercise belongs to the chapter Further AM Variants.
- Particular reference is made to the page Quadrature Amplitude Modulation (QAM).
- It is worth noting that the carrier signals $z_2(t)$ and $z_{2,\hspace{0.05cm}{\rm E}}(t)$ are applied with positive signs here.
- Often – as in the theory section – these carrier signals are given as "minus-sine".
- The following trigonometric transformations are given:
- $$ \cos(\alpha) \cdot \cos(\beta) = 1/2 \cdot \big[ \cos(\alpha - \beta)+ \cos(\alpha + \beta) \big],$$
- $$ \sin(\alpha) \cdot \sin(\beta) = 1/2 \cdot \big[ \cos(\alpha - \beta)- \cos(\alpha + \beta) \big],$$
- $$ \sin(\alpha) \cdot \cos(\beta) = 1/2 \cdot \big[ \sin(\alpha - \beta)+ \sin(\alpha + \beta) \big] \hspace{0.05cm}.$$
Questions
Solution
- $$s(t) = A_1 \cdot \cos(\omega_{\rm 1} \cdot t)\cdot \cos(\omega_{\rm T} \cdot t) + A_2 \cdot \sin(\omega_{\rm 2} \cdot t)\cdot \sin(\omega_{\rm T} \cdot t) $$
- $$\Rightarrow \hspace{0.3cm}s(t) = \frac{A_1}{2}\cdot \cos((\omega_{\rm T} - \omega_{\rm 1})\cdot t) + \frac{A_1}{2}\cdot \cos((\omega_{\rm T} + \omega_{\rm 1})\cdot t) + \frac{A_2}{2}\cdot \cos((\omega_{\rm T} - \omega_{\rm 2})\cdot t) - \frac{A_2}{2}\cdot \cos((\omega_{\rm T} + \omega_{\rm 2})\cdot t)\hspace{0.05cm}.$$
- Richtig ist demnach der zweite Lösungsvorschlag.
(2) Mit $A_1 = A_2 = 2 \ \rm V$ und $f_1 = f_2 = 5\ \rm kHz$ überlagern sich die erste und die dritte Cosinusschwingungen konstruktiv und die beiden anderen heben sich vollständig auf.
- Es ergibt sich somit das folgende einfache Ergebnis:
- $$ s(t) = 2\,{\rm V} \cdot \cos(2 \pi \cdot 20\,{\rm kHz} \cdot t) \hspace{0.3cm}\Rightarrow \hspace{0.3cm} s(t = 50\,{\rm µ s}) \hspace{0.15cm}\underline {= 2\,{\rm V}} \hspace{0.05cm}.$$
(3) Richtig ist der erste Lösungsvorschlag:
- Bei phasensynchroner Demodulation $(Δϕ_T = 0)$ erhält man für die Signale vor den Tiefpässen gemäß der Teilaufgabe (2):
- $$b_1(t) = 2\,{\rm V} \cdot \cos(\omega_{\rm 20} \cdot t)\cdot 2 \cdot \cos(\omega_{\rm 25} \cdot t) = 2\,{\rm V} \cdot \cos(\omega_{\rm 5} \cdot t) + 2\,{\rm V} \cdot \cos(\omega_{\rm 45} \cdot t),$$
- $$ b_2(t) = 2\,{\rm V} \cdot \cos(\omega_{\rm 20} \cdot t)\cdot 2 \cdot \sin(\omega_{\rm 25} \cdot t) = 2\,{\rm V} \cdot \sin(\omega_{\rm 5} \cdot t) + 2\,{\rm V} \cdot \sin(\omega_{\rm 45} \cdot t)\hspace{0.05cm}.$$
- Nach Eliminierung der jeweiligen $45\ \rm kHz$–Anteile ergibt sich somit $v_1(t) = q_1(t)$ und $v_2(t) = q_2(t)$.
(4) Analog zur Teilaufgabe (3) gilt nun:
- $$ b_1(t) = 2\,{\rm V} \cdot \cos(\omega_{\rm 20} \cdot t)\cdot 2 \cdot \cos(\omega_{\rm 25} \cdot t+ \Delta \phi_{\rm T})= 2\,{\rm V} \cdot \cos(\omega_{\rm 5} \cdot t + \Delta \phi_{\rm T}) + {(45 \,\rm kHz-Anteil )},$$
- $$b_2(t)= 2\,{\rm V} \cdot \cos(\omega_{\rm 20} \cdot t)\cdot 2 \cdot \sin(\omega_{\rm 25} \cdot t+ \Delta \phi_{\rm T})= 2\,{\rm V} \cdot \sin(\omega_{\rm 5} \cdot t + \Delta \phi_{\rm T}) + {(45 \,\rm kHz-Anteil )}\hspace{0.05cm}.$$
- Die Sinkensignale $v_1(t)$ und $v_2(t)$ weisen bei dieser Konstellation gegenüber $q_1(t)$ und $q_2(t)$ Laufzeiten und damit Phasenverzerrungen auf.
- Diese gehören zur Klasse der linearen Verzerrungen ⇒ Antwort 2.
(5) Allgemein gilt für das Empfangssignal:
- $$r(t) = s(t) = q_1(t) \cdot \cos(\omega_{\rm T} \cdot t) + q_2(t) \cdot \sin(\omega_{\rm T} \cdot t) \hspace{0.05cm}.$$
Die Multiplikation mit den empfängerseitigen Trägersignalen $z_{1,\hspace{0.05cm}{\rm E}}(t)$ und $z_{2,\hspace{0.05cm}{\rm E}}(t)$ und Bandbegrenzung führt zu den Signalen
- $$v_1(t) = \cos(\Delta \phi_{\rm T}) \cdot q_1(t) - \sin(\Delta \phi_{\rm T}) \cdot q_2(t),$$
- $$ v_2(t) = \sin(\Delta \phi_{\rm T}) \cdot q_1(t) + \cos(\Delta \phi_{\rm T}) \cdot q_2(t) \hspace{0.05cm}.$$
Daraus ist zu ersehen:
- Bei einem Phasenversatz von $Δϕ_{\rm T} = 30^\circ$ beinhaltet das Sinkensignal $v_1(t)$ nicht nur das um $\cos(30^\circ) = 0.866$ gedämpfte Signal $q_1(t)$, sondern auch die in $q_2(t)$ enthaltene Frequenz $f_2$.
- Diese ist mit dem Faktor $\sin(30^\circ) = 0.5$ gewichtet.
- Es liegen somit nichtlineare Verzerrungen vor ⇒ Antwort 3.