Difference between revisions of "Aufgaben:Exercise 2.1: Two-Dimensional Impulse Response"
m (Javier verschob die Seite Exercises:Exercise 2.1: Two-Dimensional Impulse Response nach Exercise 2.1: Two-Dimensional Impulse Response) |
|||
| Line 2: | Line 2: | ||
{{quiz-Header|Buchseite=Mobile Kommunikation/Allgemeine Beschreibung zeitvarianter Systeme}} | {{quiz-Header|Buchseite=Mobile Kommunikation/Allgemeine Beschreibung zeitvarianter Systeme}} | ||
| − | [[File:P_ID2144__Mob_A_2_1.png|right|frame| | + | [[File:P_ID2144__Mob_A_2_1.png|right|frame|Two-dimensional impulse response]] |
| − | + | It is supposed to determine the two-dimensional impulse response | |
| − | + | $$h(\dew,\hspace{0.05cm}t) = \sum_{m = 1}^{M} z_m(t) \cdot {\rm \delta} (\tau - \tau_m)$$ | |
| − | + | can be analyzed according to the adjoining diagram. The two axes are time-discrete: | |
| − | * $\tau$ | + | * $\tau$ indicates the <i>delay time</i> and can take values between $0$ and $6 \ {\rm µ s}$ in the example. |
| − | * | + | * The ''absolute time'' $t$ makes statements about the frequency of snapshots and characterizes the time variance. It holds $t = n \cdot T$, where $T \gg \tau_{\rm max}$ should hold. |
| − | + | The arrows in the graphic mark different Dirac functions with the impulse weights $1$ (red), $1/2$ (blue) and $1/4$ (green). This means that the delay time $\tau$ is also time-discrete here. | |
| − | + | When measuring the impulse responses at different times $t$ at second intervals, the resolution of the $\tau$–axis $2$ microseconds $(\delta \tau = 2 \ \rm µ s)$. The echoes were not localized more precisely. | |
| − | + | In this task the following quantities are also referred to: | |
| − | * | + | * the <i>time variant transfer function</i> according to the definition |
:$$H(f,\hspace{0.05cm} t) | :$$H(f,\hspace{0.05cm} t) | ||
| − | \hspace{0.2cm} \stackrel {f,\hspace{0.05cm}\ | + | \hspace{0.2cm} \stackrel {f,\hspace{0.05cm}{\a6}{\bullet}{\bullet\!-\!-\!-\!-\!-\!\circ} \hspace{0.2cm} h(\dew,\hspace{0.05cm}t) |
\hspace{0.05cm},$$ | \hspace{0.05cm},$$ | ||
| − | * | + | * the approximation of the <i>coherence bandwidth</i> as the reciprocal of the maximum extension of $h(\tau, t)$: |
| − | :$$B_{\rm K} \hspace{0.01cm}' = \frac{1}{\ | + | :$$B_{\rm K} \hspace{0.01cm}' = \frac{1}{\frac_{\rm max} - \dew_{\rm min}} |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| Line 30: | Line 30: | ||
| − | '' | + | ''Notes:'' |
| − | * | + | * The task belongs to the topic of the chapter [[Mobile_Communication/General_Description_time_variant_Systems| General Description of Time Variant Systems]]. |
| − | * | + | * More detailed information on various definitions for the coherence bandwidth can be found in chapter [[Mobile_Communications/The_GWSSUS%E2%80%93Channel Model|The GWSSUS–Channel Model]], especially in the sample solution for the [[Tasks:2.7_Coh%C3%A4limit Bandwidth|Task 2.7Z]]. |
| − | * | + | * It should be noted that this is a constructed task. According to the above graphic, the 2D–impulse response changes significantly during the time span $T$ seriously. Therefore $T$ is to be interpreted here as very large, for example one hour. |
| − | * | + | *In mobile radio, $h(\tau, t)$ changes in the millisecond range taking into account the Doppler effect, but the changes during this time are rather moderate. |
| − | === | + | ===Questionnaire== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {What restriction does the specification $\Delta \tau = 2 \rm µ s$ for the maximum bandwidth $B_{\rm max}$ of the message signal to be examined? |
|type="{}"} | |type="{}"} | ||
| − | $B_{\rm max} \ = \ ${ 500 3% } $\ \rm kHz$ | + | $B_{\rm max} \ = \ ${ 500 3% } $\ \ \rm kHz$ |
| − | { | + | {At what time $t_2$ is the channel ideal, characterized by $H(f, t_{\rm 2}) = 1$? |
|type="{}"} | |type="{}"} | ||
$t_{\rm 2} \ = \ ${ 0. } $\ \cdot T$ | $t_{\rm 2} \ = \ ${ 0. } $\ \cdot T$ | ||
| − | { | + | {From what time $t_{\rm 3}$ does this channel cause distortion? |
|type="{}"} | |type="{}"} | ||
$t_{\rm 3} \ = \ ${ 3 3% } $\ \cdot T$ | $t_{\rm 3} \ = \ ${ 3 3% } $\ \cdot T$ | ||
| − | { | + | {Calculate the coherence bandwidth for $t = 3T$, $t = 4T$ and $t = 5T$: |
|type="{}"} | |type="{}"} | ||
| − | $t = 3T \text{:} \hspace{0.4cm} B_{\rm K} \hspace{0.01cm}' \ = \ ${ 250 3% } $\ \rm kHz$ | + | $t = 3T \text{:} \hspace{0.4cm} B_{\rm K} \hspace{0.01cm}' \ = \ ${ 250 3% } $\ \ \rm kHz$ |
| − | $t = 4T \text{:} \hspace{0.4cm} B_{\rm K} \hspace{0.01cm}' \ = \ ${ 250 3% } $\ \rm kHz$ | + | $t = 4T \text{:} \hspace{0.4cm} B_{\rm K} \hspace{0.01cm}' \ = \ ${ 250 3% } $\ \ \rm kHz$ |
| − | $t = 5T \text{:} \hspace{0.4cm} B_{\rm K} \hspace{0.01cm}' \ = \ ${ 166.7 3% } $\ \rm kHz$ | + | $t = 5T \text{:} \hspace{0.4cm} B_{\rm K} \hspace{0.01cm}' \ = \ ${ 166.7 3% } $\ \ \rm kHz$ |
| − | { | + | {From what time $t_{\rm 5}$ could this channel be considered as time invariant? |
|type="{}"} | |type="{}"} | ||
$t_{\rm 5} \ = \ ${ 5 3% } $\ \cdot T$ | $t_{\rm 5} \ = \ ${ 5 3% } $\ \cdot T$ | ||
| − | { | + | {For which of the mentioned $T$–values does working with the $\rm 2D$–impulse response make sense? |
|type="[]"} | |type="[]"} | ||
| − | - | + | - A (slow) channel change occurs approximately after $T = 1 \ \rm µ s$. |
| − | + | + | + A (slow) channel change takes place approximately after $T = 1 \ \rm s$. |
</quiz> | </quiz> | ||
| − | === | + | ===Sample solution=== |
| − | {{ML-Kopf}} | + | {{{ML-Kopf}} |
| − | '''(1)''' | + | '''(1)''' The message signal described in the equivalent low-pass band shall not have a bandwidth greater than $B_{\rm max} = 1/\delta \tau \ \underline {= 500 \ \rm kHz}$. |
| − | * | + | *This mathematical (two-sided) bandwidth of the low pass–signal is also the maximum physical (one-sided) bandwidth of the corresponding bandpass–signal. |
| − | '''(2)''' $H(f, t_{\rm 2}) = 1$ | + | '''(2)''' $H(f, t_{\rm 2}) = 1$ means in the time domain $h(\tau, t_{\rm 2}) = \delta(\tau)$. |
| − | * | + | *Only then the channel is ideal. |
| − | * | + | *You can see from the graphic that this only applies to the time $t_{\rm 2} \ \underline {= 0}$. |
| + | '''(3)''' Distortions occur if at time $t$ the impulse response is composed of two or more Dirac functions ⇒ $t ≥ t_{\rm 3} \ \ \underline {\a6}$3T | ||
| + | *At time $t = T$ the signal $s(t)$ is delayed only by $2 \ \rm µ s$. | ||
| + | *At $t = 2T$ the amplitude is additionally reduced by $50 \%$ ($6 \ \ \rm dB$ loss). | ||
| − | |||
| − | |||
| − | |||
| − | + | '''(4)''' At time $t = 3T$ the two Dirac functions occur at $\tau_{\rm min} = 0$ and $\tau_{\rm max} = 4 \ \rm µ s$. | |
| − | + | *The (simple approximation for the) coherence bandwidth is the reciprocal of this | |
| − | '''(4)''' | + | $$B_{\rm K}\hspace{0.01cm}' = \frac{1}{4\,\,{\,}{\rm µ s} \hspace{0.25cm} \underline{ = 250\,\,\,{\rm kHz}} |
| − | * | ||
| − | |||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | * | + | *As even at the time $t = 4T$ the Dirac functions are $4 \ \rm µ s$ apart, you also get $B_{\rm K} here \hspace{0.01cm}' = \underline {250 \ \rm kHz}$. |
| − | * | + | *At $t = 5T$ the impulse response has an extension of $6 \ \ \rm µ s \ \ \Rightarrow \ {\it B}_{\rm K} \hspace{0.01cm}' \ \underline {\approx 166.7 \ \rm kHz}$. |
| − | '''(5)''' | + | '''(5)''' The impulse responses are identical at the times $5T$, $6T$ and $7T$ and consist of 3 diracs each. |
| − | * | + | * Assuming that nothing changes in this respect for $t ≥ 8T$, you get $t_{\rm 5} \ \ \underline {= 5T}$. |
| − | '''(6)''' | + | '''(6)''' Correct is the <u>solution 2</u>: |
| − | * | + | *The temporal change of the impulse response, whose dynamics is expressed by the parameter $T$, must be slow in comparison to the maximum expansion of $h(\tau, t)$, which in this task equals $\tau_{\rm max} = 6 \ \rm µ s$: &e.g; |
| − | + | $$T \gg \dew_{\rm max}.$$ | |
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | |||
[[Category:Exercises for Mobile Communications|^2.1 Description of Time-Variant Systems^]] | [[Category:Exercises for Mobile Communications|^2.1 Description of Time-Variant Systems^]] | ||
Revision as of 14:07, 15 April 2020
It is supposed to determine the two-dimensional impulse response $$h(\dew,\hspace{0.05cm}t) = \sum_{m = 1}^{M} z_m(t) \cdot {\rm \delta} (\tau - \tau_m)$$
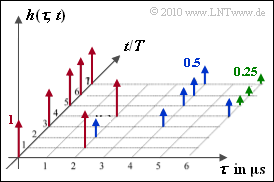
can be analyzed according to the adjoining diagram. The two axes are time-discrete:
- $\tau$ indicates the delay time and can take values between $0$ and $6 \ {\rm µ s}$ in the example.
- The absolute time $t$ makes statements about the frequency of snapshots and characterizes the time variance. It holds $t = n \cdot T$, where $T \gg \tau_{\rm max}$ should hold.
The arrows in the graphic mark different Dirac functions with the impulse weights $1$ (red), $1/2$ (blue) and $1/4$ (green). This means that the delay time $\tau$ is also time-discrete here.
When measuring the impulse responses at different times $t$ at second intervals, the resolution of the $\tau$–axis $2$ microseconds $(\delta \tau = 2 \ \rm µ s)$. The echoes were not localized more precisely.
In this task the following quantities are also referred to:
- the time variant transfer function according to the definition
- $$H(f,\hspace{0.05cm} t) \hspace{0.2cm} \stackrel {f,\hspace{0.05cm}{\a6}{\bullet}{\bullet\!-\!-\!-\!-\!-\!\circ} \hspace{0.2cm} h(\dew,\hspace{0.05cm}t) \hspace{0.05cm},$$
- the approximation of the coherence bandwidth as the reciprocal of the maximum extension of $h(\tau, t)$:
- $$B_{\rm K} \hspace{0.01cm}' = \frac{1}{\frac_{\rm max} - \dew_{\rm min}} \hspace{0.05cm}.$$
Notes:
- The task belongs to the topic of the chapter General Description of Time Variant Systems.
- More detailed information on various definitions for the coherence bandwidth can be found in chapter The GWSSUS–Channel Model, especially in the sample solution for the Task 2.7Z.
- It should be noted that this is a constructed task. According to the above graphic, the 2D–impulse response changes significantly during the time span $T$ seriously. Therefore $T$ is to be interpreted here as very large, for example one hour.
- In mobile radio, $h(\tau, t)$ changes in the millisecond range taking into account the Doppler effect, but the changes during this time are rather moderate.
=Questionnaire
Sample solution
{
- This mathematical (two-sided) bandwidth of the low pass–signal is also the maximum physical (one-sided) bandwidth of the corresponding bandpass–signal.
(2) $H(f, t_{\rm 2}) = 1$ means in the time domain $h(\tau, t_{\rm 2}) = \delta(\tau)$.
- Only then the channel is ideal.
- You can see from the graphic that this only applies to the time $t_{\rm 2} \ \underline {= 0}$.
(3) Distortions occur if at time $t$ the impulse response is composed of two or more Dirac functions ⇒ $t ≥ t_{\rm 3} \ \ \underline {\a6}$3T
- At time $t = T$ the signal $s(t)$ is delayed only by $2 \ \rm µ s$.
- At $t = 2T$ the amplitude is additionally reduced by $50 \%$ ($6 \ \ \rm dB$ loss).
(4) At time $t = 3T$ the two Dirac functions occur at $\tau_{\rm min} = 0$ and $\tau_{\rm max} = 4 \ \rm µ s$.
- The (simple approximation for the) coherence bandwidth is the reciprocal of this
$$B_{\rm K}\hspace{0.01cm}' = \frac{1}{4\,\,{\,}{\rm µ s} \hspace{0.25cm} \underline{ = 250\,\,\,{\rm kHz}} \hspace{0.05cm}.$$
- As even at the time $t = 4T$ the Dirac functions are $4 \ \rm µ s$ apart, you also get $B_{\rm K} here \hspace{0.01cm}' = \underline {250 \ \rm kHz}$.
- At $t = 5T$ the impulse response has an extension of $6 \ \ \rm µ s \ \ \Rightarrow \ {\it B}_{\rm K} \hspace{0.01cm}' \ \underline {\approx 166.7 \ \rm kHz}$.
(5) The impulse responses are identical at the times $5T$, $6T$ and $7T$ and consist of 3 diracs each.
- Assuming that nothing changes in this respect for $t ≥ 8T$, you get $t_{\rm 5} \ \ \underline {= 5T}$.
(6) Correct is the solution 2:
- The temporal change of the impulse response, whose dynamics is expressed by the parameter $T$, must be slow in comparison to the maximum expansion of $h(\tau, t)$, which in this task equals $\tau_{\rm max} = 6 \ \rm µ s$: &e.g;
$$T \gg \dew_{\rm max}.$$