Difference between revisions of "Aufgaben:Exercise 2.1Z: Distortion and Equalisation"
From LNTwww
m (Guenter verschob die Seite 2.1Z Verzerrung und Entzerrung nach Aufgabe 2.1Z: Verzerrung und Entzerrung) |
m (Text replacement - "equalisation" to "equalization") |
||
| (23 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Linear_and_Time_Invariant_Systems/Classification_of_the_Distortions |
}} | }} | ||
| − | [[File:P_ID880__LZI_Z_2_1.png|right| | + | [[File:P_ID880__LZI_Z_2_1.png|right|frame|Three continuous spectral functions]] |
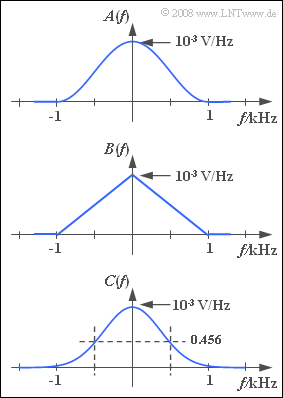
| − | + | Three continuous spectral functions are depicted in the graph: | |
| − | * | + | * a cos<sup>2</sup>–spectrum that has components only in the range $|f| < 1 \ \rm kHz$ where the following holds: |
| − | :$$A(f) = 10^{\rm -3} \ | + | :$$A(f) = 10^{\rm -3} \ {\rm V}/{\rm Hz} \cdot \cos^2(\frac{|f|}{1 \, \rm kHz} \cdot \frac{\pi}{ 2} ) ,$$ |
| − | * | + | * a triangular spectrum which is also limited to the frequency range $|f| < 1 \ \rm kHz$: |
| − | :$$B(f) = 10^{\rm -3} \ | + | :$$B(f) = 10^{\rm -3} \ {\rm V}/{\rm Hz} \cdot \left(1-\frac{|f|}{1 \, \rm kHz} \right),$$ |
| − | * | + | * a so-called Gaussian spectrum: |
| − | :$$C(f) = 10^{\rm -3} \ | + | :$$C(f) = 10^{\rm -3} \ {\rm V}/{\rm Hz} \cdot {\rm e}^{-\pi \hspace{0.05cm}\cdot \hspace{0.05cm} (f/{1 \, \rm kHz})^2} .$$ |
| − | |||
| − | |||
| − | |||
| + | Furthermore, we consider | ||
| + | *a linearly distorting system $S_{\rm V}$ with $X(f)$ at the input and $Y(f)$ at the output, and | ||
| + | *the equalization system $S_{\rm E}$ with the input spectrum $Y(f)$ and output spectrum $Z(f)$. | ||
| − | |||
| − | |||
| + | The frequency responses of the two systems $S_{\rm V}$ and $S_{\rm E}$ are: | ||
| + | :$$H_{\rm V}(f) = \frac{Y(f)}{X(f)} , \hspace{0.3cm}$$ | ||
| + | :$$H_{\rm E}(f) = \frac{Z(f)}{Y(f)} .$$ | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | === | + | |
| + | |||
| + | |||
| + | ''Please note:'' | ||
| + | *The exercise belongs to the chapter [[Linear_and_Time_Invariant_Systems/Classification_of_the_Distortions|Classification of the Distortions]]. | ||
| + | *A complete equalization means that $Z(f) = X(f)$ holds. | ||
| + | |||
| + | |||
| + | |||
| + | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Is the constellation $X(f) = A(f)$ and $Y(f) = B(f)$ possible with a linear system? Justify your answer. |
| − | |type=" | + | |type="()"} |
| − | + | + | + Yes. |
| − | - | + | - No. |
| − | { | + | {$X(f) = A(f)$ and $Y(f) = B(f)$ still hold true. Is complete equalization possible with a linear filter $H_{\rm E}(f)$ ? <br>If YES, please specify $H_{\rm E}(f)$. |
| − | |type=" | + | |type="()"} |
| − | + | + | + Yes. |
| − | - | + | - No. |
| − | { | + | {Is the constellation $X(f) = C(f)$ and $Y(f) = B(f)$ possible with a linear system? Justify your answer. |
| − | |type=" | + | |type="()"} |
| − | + | + | + Yes. |
| − | - | + | - No. |
| − | { | + | {$X(f) = C(f)$ und $Y(f) = B(f)$ still hold true. Is complete equalization possible with a linear filter $H_{\rm E}(f)$ ? <br>If YES, please specify $H_{\rm E}(f)$ . |
| − | |type=" | + | |type="()"} |
| − | - | + | - Yes. |
| − | + | + | + No. |
| − | { | + | {Is the constellation $X(f) = A(f)$ and $Y(f) = C(f)$ possible with a linear system? <br>Justify your answer. |
| − | |type=" | + | |type="()"} |
| − | - | + | - Yes. |
| − | + | + | + No. |
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' <u>Yes</u> is correct: |
| − | + | *This constellation is possible because $X(f)$ is also always different from zero for all $Y(f) \ne 0$ . | |
| − | * | + | *For all frequencies less than $0.5 \ \rm kHz$ , $H_{\rm V} = B(f)/A(f) < 1$ causes an attenuation. |
| + | *In contrast, the frequencies between $0.5 \ \rm kHz$ and $1 \ \rm kHz$ are amplified by the system. | ||
| + | |||
| + | |||
| + | |||
| + | '''(2)''' <u>Yes</u> is correct: | ||
| + | *For this constellation, a complete linear equalization is also possible with | ||
| + | :$$H_{\rm E}(f) = \frac{Z(f)}{Y(f)} = \frac{A(f)}{B(f)} = \frac{1}{H_{\rm V}(f)}$$ | ||
| + | :since both spectra extend exactly up to $1 \ \rm kHz$ . | ||
| − | |||
| − | |||
| − | |||
| + | '''(3)''' <u>Yes</u> is correct: | ||
| + | *This constellation is possible, too. The filter $H_{\rm V}(f)$ must form a triangular spectrum for the frequencies $|f| <1 \ \rm kHz$ out of the Gaussian spectrum and suppress all frequencies $|f| > 1 \ \rm kHz$ . | ||
| − | |||
| − | '''(4)''' | + | '''(4)''' <u>No</u> is correct: |
| + | *A complete equalization is not possible here: | ||
| + | *The parts of the Gaussian spectrum, which are completely eliminated by $H_{\rm V}(f)$ , cannot be recovered by the linear system. | ||
| − | |||
| − | + | '''(5)''' <u>No</u> is correct: | |
| + | *This constellation is not possible with a linear system since there cannot be any spectral components included in the spectrum $C(f) = A(f) \cdot H_{\rm V}(f)$ that do not exist in $A(f)$ . | ||
| + | *The question whether there is a non-linear system which forms a Gaussian spectrum out of the $\cos^2$-spectrum is not asked and therefore does not need to be answered: The authors rather believe "no". | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category: | + | [[Category:Linear and Time-Invariant Systems: Exercises|^2.1 Classification of the Distortions^]] |
Latest revision as of 14:50, 21 September 2021
Three continuous spectral functions are depicted in the graph:
- a cos2–spectrum that has components only in the range $|f| < 1 \ \rm kHz$ where the following holds:
- $$A(f) = 10^{\rm -3} \ {\rm V}/{\rm Hz} \cdot \cos^2(\frac{|f|}{1 \, \rm kHz} \cdot \frac{\pi}{ 2} ) ,$$
- a triangular spectrum which is also limited to the frequency range $|f| < 1 \ \rm kHz$:
- $$B(f) = 10^{\rm -3} \ {\rm V}/{\rm Hz} \cdot \left(1-\frac{|f|}{1 \, \rm kHz} \right),$$
- a so-called Gaussian spectrum:
- $$C(f) = 10^{\rm -3} \ {\rm V}/{\rm Hz} \cdot {\rm e}^{-\pi \hspace{0.05cm}\cdot \hspace{0.05cm} (f/{1 \, \rm kHz})^2} .$$
Furthermore, we consider
- a linearly distorting system $S_{\rm V}$ with $X(f)$ at the input and $Y(f)$ at the output, and
- the equalization system $S_{\rm E}$ with the input spectrum $Y(f)$ and output spectrum $Z(f)$.
The frequency responses of the two systems $S_{\rm V}$ and $S_{\rm E}$ are:
- $$H_{\rm V}(f) = \frac{Y(f)}{X(f)} , \hspace{0.3cm}$$
- $$H_{\rm E}(f) = \frac{Z(f)}{Y(f)} .$$
Please note:
- The exercise belongs to the chapter Classification of the Distortions.
- A complete equalization means that $Z(f) = X(f)$ holds.
Questions
Solution
(1) Yes is correct:
- This constellation is possible because $X(f)$ is also always different from zero for all $Y(f) \ne 0$ .
- For all frequencies less than $0.5 \ \rm kHz$ , $H_{\rm V} = B(f)/A(f) < 1$ causes an attenuation.
- In contrast, the frequencies between $0.5 \ \rm kHz$ and $1 \ \rm kHz$ are amplified by the system.
(2) Yes is correct:
- For this constellation, a complete linear equalization is also possible with
- $$H_{\rm E}(f) = \frac{Z(f)}{Y(f)} = \frac{A(f)}{B(f)} = \frac{1}{H_{\rm V}(f)}$$
- since both spectra extend exactly up to $1 \ \rm kHz$ .
(3) Yes is correct:
- This constellation is possible, too. The filter $H_{\rm V}(f)$ must form a triangular spectrum for the frequencies $|f| <1 \ \rm kHz$ out of the Gaussian spectrum and suppress all frequencies $|f| > 1 \ \rm kHz$ .
(4) No is correct:
- A complete equalization is not possible here:
- The parts of the Gaussian spectrum, which are completely eliminated by $H_{\rm V}(f)$ , cannot be recovered by the linear system.
(5) No is correct:
- This constellation is not possible with a linear system since there cannot be any spectral components included in the spectrum $C(f) = A(f) \cdot H_{\rm V}(f)$ that do not exist in $A(f)$ .
- The question whether there is a non-linear system which forms a Gaussian spectrum out of the $\cos^2$-spectrum is not asked and therefore does not need to be answered: The authors rather believe "no".