Aufgaben:Exercise 2.2Z: Distortion Power again

• Return to book

Concerning the computation of the distortion power

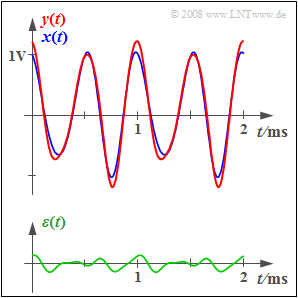
At the input of the considered functional unit, which is not specified in more detail, there is the periodic signal $x(t)$  shown in blue in the graph. This is given by the spectrum of the corresponding analytical signal:

$$X_+(f) = {1 \,\rm V} \cdot {\rm \delta}(f- {2 \,\rm kHz}) + {0.2 \,\rm V} \cdot {\rm e}^{\rm j \hspace{0.05cm}\cdot \hspace{0.05cm}90^{\circ} } \cdot \delta(f- {3 \,\rm kHz}).$$

This spectral function is obtained from the usual spectrum $X(f)$,  by

• truncating all components at negative frequencies,  and
• doubling the components at positive frequencies.

For more details on the analytical signal and its spectrum, see the chapter  Analytical Signal and its Spectral Function  of the book "Signal Representation".
The spectrum of the analytical signal at the output of the functional unit is:

$$Y_+(f) = {1.1 \,\rm V} \cdot {\rm \delta}(f- {2 \,\rm kHz}) + {0.25 \,\rm V} \cdot {\rm e}^{\rm j \hspace{0.05cm}\cdot \hspace{0.05cm} 60^{\circ} } \cdot \delta(f- {3 \,\rm kHz})+ {0.05 \,\rm V} \cdot {\rm e}^{-\rm j \hspace{0.05cm}\cdot \hspace{0.05cm} 90^{\circ} } \cdot \delta(f- {5 \,\rm kHz}).$$

Die untere Skizze zeigt das Differenzsignal  $\varepsilon(t) = y(t) - x(t)$.  Ein Maß für die im System entstandenen Verzerrungen ist die auf den Widerstand  $R = 1 \ \rm \Omega$  bezogene "Verzerrungsleistung".

$$P_{\rm V} = \overline{\varepsilon^2(t)} = \frac{1}{T_{\rm 0}} \cdot \int_{0}^{ T_{\rm 0}} {\varepsilon^2(t) }\hspace{0.1cm}{\rm d}t.$$

Anzumerken ist, dass die Verzerrungsleistung auch im Spektralbereich berechnet werden kann – und hier zudem einfacher.

In analoger Weise ist die Leistung  $P_x$  des Eingangssignals  $x(t)$  definiert.  Als quantitatives Maß für die Stärke der Verzerrungen wird das Signal–zu–Verzerrungs–Leistungsverhältnis angegeben, das meistens logarithmisch (in dB) dargestellt wird:

$$10 \cdot {\rm lg} \hspace{0.1cm}\rho_{\rm V} = 10 \cdot {\rm lg} \hspace{0.1cm}{ P_{x}}/{P_{\rm V}} \hspace{0.05cm}.$$

Please note:

• The exercise belongs to the chapter  Classification of the Distortions.

• Alle hier abgefragten Leistungen beziehen sich auf den Widerstand  $R = 1 \ \rm \Omega$  und haben somit die Einheit  ${\rm V}^2$.
• Die Leistung eines (reellen) Signals  $x(t)$  kann auch aus der Spektralfunktion  $X(f)$  berechnet werden:

$$P_{x} =\frac{1}{T_{\rm 0}} \cdot\int_{-\infty}^{ \infty} x^2(t)\hspace{0.1cm}{\rm d}t = \frac{1}{T_{\rm 0}} \cdot \int_{-\infty}^{ \infty} |X(f)|^2\hspace{0.1cm}{\rm d}f.$$

Questions

1

Welche Aussagen sind bezüglich des Signals  $x(t)$  zutreffend?

	Es ist  $x(t) = 1 \ { \rm V} \cdot {\rm cos}(2\pi \cdot 2 \ {\rm kHz} \cdot t ) + 0.2 \ { \rm V} \cdot {\rm cos}(2\pi \cdot 3 \ {\rm kHz} \cdot t )$.
	Die Periodendauer ist  $T_0 = 1 \ \rm ms$.
	Die Periodendauer ist  $T_0 = 2 \ \rm ms$.

2

Berechnen Sie die Leistung  $P_x$  des Eingangssignals  $x(t)$.

$P_x \ = \ $ $\ \rm V^2$

3

Berechnen Sie die Verzerrungsleistung  $P_{\rm V}$.

$P_{\rm V} \ = \ $ $\ \rm V^2$

4

Berechnen Sie das Signal–zu–Verzerrungs–Leistungsverhältnis  $\rho_{\rm V}$  und geben Sie dieses als dB–Wert ein.

$10 \cdot {\rm lg} \ \rho_{\rm V} \ = \ $ $\ \rm dB$

Solution

Solution

(1)  Richtig ist die Antwort 2:

• Der größte gemeinsame Teiler von  $f_1 = 2 \ \rm kHz$  und  $f_2 = 3 \ \rm kHz$  ist  $f_0 = 1 \ \rm kHz$.
• Damit beträgt die Periodendauer  $T_0 = 1/f_0 = 1 \ \rm ms$.
• Das Signal lautet aufgrund des Phasenterms  ${\rm e}^{{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}90^\circ}$:

$$x(t) = {1 \, \rm V} \cdot {\rm cos}(2\pi f_1 t ) - {0.2 \, \rm V} \cdot {\rm sin}(2\pi f_2 t ).$$

(2)  Um die Leistung im Zeitbereich zu berechnen, muss das Signal  $x(t) = x_1(t) + x_2(t)$  quadriert und über ein geeignetes Zeitintervall gemittelt werden. 

• Für ein periodisches Signal genügt die Mittelung über  $T_0$:

$$P_{\rm V} = \frac{1}{T_{\rm 0}} \cdot \int_{0}^{ T_{\rm 0}} {\left[x_1(t)+ x_2(t) \right]^2 }\hspace{0.1cm}{\rm d}t = \frac{1}{T_{\rm 0}} \cdot \int_{0}^{ T_{\rm 0}} {x_1^2(t) }\hspace{0.1cm}{\rm d}t \hspace{0.1cm}+\hspace{0.1cm} \frac{1}{T_{\rm 0}} \cdot \int_{0}^{ T_{\rm 0}} {x_2^2(t) }\hspace{0.1cm}{\rm d}t \hspace{0.1cm}+\hspace{0.1cm} \frac{2}{T_{\rm 0}} \cdot \int_{0}^{ T_{\rm 0}} { x_1(t) \cdot x_2(t) }\hspace{0.1cm}{\rm d}t.$$

• Das erste Integral liefert:

$$P_{\rm 1} = \frac{1}{T_{\rm 0}} \cdot \int_{0}^{ T_{\rm 0}} { ({1 \, \rm V})^2 \cdot {\rm cos}^2(2\pi f_1 t )}\hspace{0.1cm}{\rm d}t = \frac{1 \, \rm V^2}{2 T_{\rm 0}}\hspace{0.05cm} \cdot \int\limits_{0}^{ T_{\rm 0}} { \left[ 1+ {\rm cos}(4\pi f_1 t )\right]}\hspace{0.1cm}{\rm d}t = {0.5 \, \rm V^2}.$$

• In gleicher Weise erhält man für die Leistung des zweiten Terms:   $P_2 = (0.2 \ {\rm V})^2/2 = 0.02 \ {\rm V}^2.$ 
• Das letzte Integral liefert keinen Beitrag, da  $x_1(t)$  und  $x_2(t)$  zueinander orthogonal sind.  Somit erhält man für die gesamte Signalleistung:

$$P_{x} =P_{\rm 1} + P_{\rm 2} = {0.5 \, \rm V^2} + {0.02 \, \rm V^2}\hspace{0.15cm}\underline{ = {0.52 \, \rm V^2}}.$$

Dieses Ergebnis kann man auch aus der Spektralfunktion herleiten, wenn man die Amplituden aller diskreten Spektralanteile quadriert, halbiert und aufsummiert. Die Phasenlagen der einzelnen Spektrallinien müssen dabei nicht berücksichtigt werden.

(3)  Unabhängig davon, ob ein lineares oder ein nichtlineares System vorliegt, kann für das analytische Spektrum des Differenzsignals $\varepsilon(t) = y(t) - x(t)$  mit  $f_2 = 2 \ \rm kHz$,  $f_3 = 3 \ \rm kHz$  und  $f_5 = 5 \ \rm kHz$  geschrieben werden:

$$E_+(f) = Y_+(f) - X_+(f) = {0.1 \,\rm V} \cdot {\rm \delta}(f- f_2) + \left[{0.25 \,\rm V} \cdot {\rm e}^{\rm j \cdot 60^{\circ} } - {0.2 \,\rm V} \cdot {\rm e}^{\rm j \cdot 90^{\circ} } \right] \cdot \delta(f- f_3) + {0.05 \,\rm V} \cdot {\rm e}^{-\rm j \cdot 90^{\circ} } \cdot \delta(f- f_5).$$

• Die komplexe Amplitude des zweiten Terms ist:

$$C_2 = {0.25 \,\rm V} \cdot \cos( 60^{\circ}) + {\rm j} \cdot{0.25 \,\rm V} \cdot \sin( 60^{\circ}) - {\rm j} \cdot{0.05 \,\rm V} $$

$$\Rightarrow \hspace{0.3cm} C_2 = {0.25 \,\rm V} \cdot 0.5 + {\rm j} \cdot{0.25 \,\rm V} \cdot 0.866 - {\rm j} \cdot{0.2 \,\rm V} = {0.125 \,\rm V} + {\rm j} \cdot{0.016 \,\rm V}.$$

• Damit ergibt sich für den Betrag:

$$|C_2| = \sqrt{({0.125 \,\rm V})^2+({0.016 \,\rm V})^2 }= {0.126 \,\rm V}.$$

• Die Phasenlagen müssen bei der Leistungsberechnung nicht berücksichtigt werden. Somit gilt:

$$P_{\rm V} = \frac{1}{2} \cdot \left[ ({0.1 \,\rm V})^2 + ({0.126 \,\rm V})^2 + ({0.05 \,\rm V})^2\right] \hspace{0.15cm}\underline{= {0.0142 \, \rm V^2}}.$$

(4)  Entsprechend der Definition auf der Angabenseite gilt:

$$\rho_{\rm V} = \frac{ P_{x}}{P_{\rm V}}= \frac{ {0.52 \, \rm V^2}}{0.0142 \, \rm V^2}\hspace{0.05cm}\rm = 36.65\hspace{0.3cm} \Rightarrow \hspace{0.3cm} 10 \cdot {\rm lg}\hspace{0.1cm}\rho_{\rm V} \hspace{0.15cm}\underline{= {15.64 \, \rm dB}}.$$