Difference between revisions of "Aufgaben:Exercise 2.2Z: Distortion Power again"
| Line 24: | Line 24: | ||
It should be noted that the distortion power can also be calculated in the spectral domain – in fact in a simpler way here. | It should be noted that the distortion power can also be calculated in the spectral domain – in fact in a simpler way here. | ||
| − | The power $P_x$ of the input signal $x(t)$ is defined in an analogous way. | + | The power $P_x$ of the input signal $x(t)$ is defined in an analogous way. As a quantitative measure of the strength of the distortions the signal–to–distortion–power ratio is specified, which is usually expressed logarithmically (in dB): |
:$$10 \cdot {\rm lg} \hspace{0.1cm}\rho_{\rm V} = 10 \cdot {\rm lg} \hspace{0.1cm}{ P_{x}}/{P_{\rm V}} \hspace{0.05cm}.$$ | :$$10 \cdot {\rm lg} \hspace{0.1cm}\rho_{\rm V} = 10 \cdot {\rm lg} \hspace{0.1cm}{ P_{x}}/{P_{\rm V}} \hspace{0.05cm}.$$ | ||
| Line 37: | Line 37: | ||
*The exercise belongs to the chapter [[Linear_and_Time_Invariant_Systems/Classification_of_the_Distortions|Classification of the Distortions]]. | *The exercise belongs to the chapter [[Linear_and_Time_Invariant_Systems/Classification_of_the_Distortions|Classification of the Distortions]]. | ||
| − | * | + | *All powers queried here refer to the resistance $R = 1 \ \rm \Omega$ and thus have the unit ${\rm V}^2$. |
| − | * | + | *The power of a (real) signal $x(t)$ can also be computed using the spectral function $X(f)$ : |
:$$P_{x} =\frac{1}{T_{\rm 0}} \cdot\int_{-\infty}^{ \infty} | :$$P_{x} =\frac{1}{T_{\rm 0}} \cdot\int_{-\infty}^{ \infty} | ||
x^2(t)\hspace{0.1cm}{\rm d}t | x^2(t)\hspace{0.1cm}{\rm d}t | ||
| Line 48: | Line 48: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Which statements are true regarding the signal $x(t)$ ? |
|type="[]"} | |type="[]"} | ||
| − | - | + | - It is $x(t) = 1 \ { \rm V} \cdot {\rm cos}(2\pi \cdot 2 \ {\rm kHz} \cdot t ) + 0.2 \ { \rm V} \cdot {\rm cos}(2\pi \cdot 3 \ {\rm kHz} \cdot t )$. |
| − | + | + | + The period is $T_0 = 1 \ \rm ms$. |
| − | - | + | - The period is $T_0 = 2 \ \rm ms$. |
| − | { | + | {Compute the power $P_x$ of the input signal $x(t)$. |
|type="{}"} | |type="{}"} | ||
$P_x \ = \ $ { 0.52 3% } $\ \rm V^2$ | $P_x \ = \ $ { 0.52 3% } $\ \rm V^2$ | ||
| − | { | + | {Compute the distortion power $P_{\rm V}$. |
|type="{}"} | |type="{}"} | ||
$P_{\rm V} \ = \ $ { 0.0142 3% } $\ \rm V^2$ | $P_{\rm V} \ = \ $ { 0.0142 3% } $\ \rm V^2$ | ||
| − | { | + | {Compute the signal–to–distortion–power ratio $\rho_{\rm V}$ and specify it as a dB–value. |
|type="{}"} | |type="{}"} | ||
$10 \cdot {\rm lg} \ \rho_{\rm V} \ = \ $ { 15.64 3% } $\ \rm dB$ | $10 \cdot {\rm lg} \ \rho_{\rm V} \ = \ $ { 15.64 3% } $\ \rm dB$ | ||
| Line 75: | Line 75: | ||
===Solution=== | ===Solution=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' <u>Answer 2</u> is correct: |
| − | * | + | *The greatest common divisor of $f_1 = 2 \ \rm kHz$ and $f_2 = 3 \ \rm kHz$ is $f_0 = 1 \ \rm kHz$. |
| − | * | + | *Hence, the period is $T_0 = 1/f_0 = 1 \ \rm ms$. |
| − | * | + | *Due to the phase term ${\rm e}^{{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}90^\circ}$ the signal is: |
:$$x(t) = {1 \, \rm V} \cdot {\rm cos}(2\pi f_1 t ) - {0.2 \, \rm | :$$x(t) = {1 \, \rm V} \cdot {\rm cos}(2\pi f_1 t ) - {0.2 \, \rm | ||
V} \cdot {\rm sin}(2\pi f_2 t ).$$ | V} \cdot {\rm sin}(2\pi f_2 t ).$$ | ||
| Line 84: | Line 84: | ||
| − | '''(2)''' | + | '''(2)''' To compute the power in the time domain the signal $x(t) = x_1(t) + x_2(t)$ must be squared and averaged over a suitable time interval. |
| − | * | + | *Averaging over $T_0$ is sufficient for a periodic signal: |
:$$P_{\rm V} = \frac{1}{T_{\rm 0}} \cdot \int_{0}^{ T_{\rm 0}} | :$$P_{\rm V} = \frac{1}{T_{\rm 0}} \cdot \int_{0}^{ T_{\rm 0}} | ||
{\left[x_1(t)+ x_2(t) \right]^2 }\hspace{0.1cm}{\rm d}t | {\left[x_1(t)+ x_2(t) \right]^2 }\hspace{0.1cm}{\rm d}t | ||
| Line 95: | Line 95: | ||
{ x_1(t) \cdot x_2(t) }\hspace{0.1cm}{\rm d}t.$$ | { x_1(t) \cdot x_2(t) }\hspace{0.1cm}{\rm d}t.$$ | ||
| − | * | + | *The first integral yields: |
:$$P_{\rm 1} = \frac{1}{T_{\rm 0}} \cdot \int_{0}^{ T_{\rm 0}} | :$$P_{\rm 1} = \frac{1}{T_{\rm 0}} \cdot \int_{0}^{ T_{\rm 0}} | ||
{ ({1 \, \rm V})^2 \cdot {\rm cos}^2(2\pi f_1 t )}\hspace{0.1cm}{\rm | { ({1 \, \rm V})^2 \cdot {\rm cos}^2(2\pi f_1 t )}\hspace{0.1cm}{\rm | ||
| Line 103: | Line 103: | ||
d}t = {0.5 \, \rm V^2}.$$ | d}t = {0.5 \, \rm V^2}.$$ | ||
| − | *In | + | *In the same way, the following is obtained for the power of the second term: $P_2 = (0.2 \ {\rm V})^2/2 = 0.02 \ {\rm V}^2.$ |
| − | * | + | *The last integral vanishes since $x_1(t)$ and $x_2(t)$ are orthogonal to each other. Consequently, the following is obtained for the total signal power: |
:$$P_{x} =P_{\rm 1} + P_{\rm 2} = {0.5 \, \rm V^2} + {0.02 \, \rm V^2}\hspace{0.15cm}\underline{ = {0.52 \, \rm V^2}}.$$ | :$$P_{x} =P_{\rm 1} + P_{\rm 2} = {0.5 \, \rm V^2} + {0.02 \, \rm V^2}\hspace{0.15cm}\underline{ = {0.52 \, \rm V^2}}.$$ | ||
Revision as of 23:37, 12 September 2021
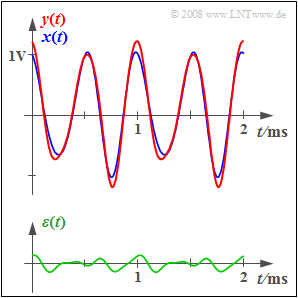
At the input of the considered functional unit, which is not specified in more detail, there is the periodic signal $x(t)$ shown in blue in the graph. This is given by the spectrum of the corresponding analytical signal:
- $$X_+(f) = {1 \,\rm V} \cdot {\rm \delta}(f- {2 \,\rm kHz}) + {0.2 \,\rm V} \cdot {\rm e}^{\rm j \hspace{0.05cm}\cdot \hspace{0.05cm}90^{\circ} } \cdot \delta(f- {3 \,\rm kHz}).$$
This spectral function is obtained from the usual spectrum $X(f)$, by
- truncating all components at negative frequencies, and
- doubling the components at positive frequencies.
For more details on the analytical signal and its spectrum, see the chapter Analytical Signal and its Spectral Function of the book "Signal Representation".
The spectrum of the analytical signal at the output of the functional unit is:
- $$Y_+(f) = {1.1 \,\rm V} \cdot {\rm \delta}(f- {2 \,\rm kHz}) + {0.25 \,\rm V} \cdot {\rm e}^{\rm j \hspace{0.05cm}\cdot \hspace{0.05cm} 60^{\circ} } \cdot \delta(f- {3 \,\rm kHz})+ {0.05 \,\rm V} \cdot {\rm e}^{-\rm j \hspace{0.05cm}\cdot \hspace{0.05cm} 90^{\circ} } \cdot \delta(f- {5 \,\rm kHz}).$$
The bottom sketch shows the difference signal $\varepsilon(t) = y(t) - x(t)$. A measure of the distortion created in the system is the "distortion power" referenced to the resistance $R = 1 \ \rm \Omega$ .
- $$P_{\rm V} = \overline{\varepsilon^2(t)} = \frac{1}{T_{\rm 0}} \cdot \int_{0}^{ T_{\rm 0}} {\varepsilon^2(t) }\hspace{0.1cm}{\rm d}t.$$
It should be noted that the distortion power can also be calculated in the spectral domain – in fact in a simpler way here.
The power $P_x$ of the input signal $x(t)$ is defined in an analogous way. As a quantitative measure of the strength of the distortions the signal–to–distortion–power ratio is specified, which is usually expressed logarithmically (in dB):
- $$10 \cdot {\rm lg} \hspace{0.1cm}\rho_{\rm V} = 10 \cdot {\rm lg} \hspace{0.1cm}{ P_{x}}/{P_{\rm V}} \hspace{0.05cm}.$$
Please note:
- The exercise belongs to the chapter Classification of the Distortions.
- All powers queried here refer to the resistance $R = 1 \ \rm \Omega$ and thus have the unit ${\rm V}^2$.
- The power of a (real) signal $x(t)$ can also be computed using the spectral function $X(f)$ :
- $$P_{x} =\frac{1}{T_{\rm 0}} \cdot\int_{-\infty}^{ \infty} x^2(t)\hspace{0.1cm}{\rm d}t = \frac{1}{T_{\rm 0}} \cdot \int_{-\infty}^{ \infty} |X(f)|^2\hspace{0.1cm}{\rm d}f.$$
Questions
Solution
- The greatest common divisor of $f_1 = 2 \ \rm kHz$ and $f_2 = 3 \ \rm kHz$ is $f_0 = 1 \ \rm kHz$.
- Hence, the period is $T_0 = 1/f_0 = 1 \ \rm ms$.
- Due to the phase term ${\rm e}^{{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}90^\circ}$ the signal is:
- $$x(t) = {1 \, \rm V} \cdot {\rm cos}(2\pi f_1 t ) - {0.2 \, \rm V} \cdot {\rm sin}(2\pi f_2 t ).$$
(2) To compute the power in the time domain the signal $x(t) = x_1(t) + x_2(t)$ must be squared and averaged over a suitable time interval.
- Averaging over $T_0$ is sufficient for a periodic signal:
- $$P_{\rm V} = \frac{1}{T_{\rm 0}} \cdot \int_{0}^{ T_{\rm 0}} {\left[x_1(t)+ x_2(t) \right]^2 }\hspace{0.1cm}{\rm d}t = \frac{1}{T_{\rm 0}} \cdot \int_{0}^{ T_{\rm 0}} {x_1^2(t) }\hspace{0.1cm}{\rm d}t \hspace{0.1cm}+\hspace{0.1cm} \frac{1}{T_{\rm 0}} \cdot \int_{0}^{ T_{\rm 0}} {x_2^2(t) }\hspace{0.1cm}{\rm d}t \hspace{0.1cm}+\hspace{0.1cm} \frac{2}{T_{\rm 0}} \cdot \int_{0}^{ T_{\rm 0}} { x_1(t) \cdot x_2(t) }\hspace{0.1cm}{\rm d}t.$$
- The first integral yields:
- $$P_{\rm 1} = \frac{1}{T_{\rm 0}} \cdot \int_{0}^{ T_{\rm 0}} { ({1 \, \rm V})^2 \cdot {\rm cos}^2(2\pi f_1 t )}\hspace{0.1cm}{\rm d}t = \frac{1 \, \rm V^2}{2 T_{\rm 0}}\hspace{0.05cm} \cdot \int\limits_{0}^{ T_{\rm 0}} { \left[ 1+ {\rm cos}(4\pi f_1 t )\right]}\hspace{0.1cm}{\rm d}t = {0.5 \, \rm V^2}.$$
- In the same way, the following is obtained for the power of the second term: $P_2 = (0.2 \ {\rm V})^2/2 = 0.02 \ {\rm V}^2.$
- The last integral vanishes since $x_1(t)$ and $x_2(t)$ are orthogonal to each other. Consequently, the following is obtained for the total signal power:
- $$P_{x} =P_{\rm 1} + P_{\rm 2} = {0.5 \, \rm V^2} + {0.02 \, \rm V^2}\hspace{0.15cm}\underline{ = {0.52 \, \rm V^2}}.$$
Dieses Ergebnis kann man auch aus der Spektralfunktion herleiten, wenn man die Amplituden aller diskreten Spektralanteile quadriert, halbiert und aufsummiert. Die Phasenlagen der einzelnen Spektrallinien müssen dabei nicht berücksichtigt werden.
(3) Unabhängig davon, ob ein lineares oder ein nichtlineares System vorliegt, kann für das analytische Spektrum des Differenzsignals $\varepsilon(t) = y(t) - x(t)$ mit $f_2 = 2 \ \rm kHz$, $f_3 = 3 \ \rm kHz$ und $f_5 = 5 \ \rm kHz$ geschrieben werden:
- $$E_+(f) = Y_+(f) - X_+(f) = {0.1 \,\rm V} \cdot {\rm \delta}(f- f_2) + \left[{0.25 \,\rm V} \cdot {\rm e}^{\rm j \cdot 60^{\circ} } - {0.2 \,\rm V} \cdot {\rm e}^{\rm j \cdot 90^{\circ} } \right] \cdot \delta(f- f_3) + {0.05 \,\rm V} \cdot {\rm e}^{-\rm j \cdot 90^{\circ} } \cdot \delta(f- f_5).$$
- Die komplexe Amplitude des zweiten Terms ist:
- $$C_2 = {0.25 \,\rm V} \cdot \cos( 60^{\circ}) + {\rm j} \cdot{0.25 \,\rm V} \cdot \sin( 60^{\circ}) - {\rm j} \cdot{0.05 \,\rm V} $$
- $$\Rightarrow \hspace{0.3cm} C_2 = {0.25 \,\rm V} \cdot 0.5 + {\rm j} \cdot{0.25 \,\rm V} \cdot 0.866 - {\rm j} \cdot{0.2 \,\rm V} = {0.125 \,\rm V} + {\rm j} \cdot{0.016 \,\rm V}.$$
- Damit ergibt sich für den Betrag:
- $$|C_2| = \sqrt{({0.125 \,\rm V})^2+({0.016 \,\rm V})^2 }= {0.126 \,\rm V}.$$
- Die Phasenlagen müssen bei der Leistungsberechnung nicht berücksichtigt werden. Somit gilt:
- $$P_{\rm V} = \frac{1}{2} \cdot \left[ ({0.1 \,\rm V})^2 + ({0.126 \,\rm V})^2 + ({0.05 \,\rm V})^2\right] \hspace{0.15cm}\underline{= {0.0142 \, \rm V^2}}.$$
(4) Entsprechend der Definition auf der Angabenseite gilt:
- $$\rho_{\rm V} = \frac{ P_{x}}{P_{\rm V}}= \frac{ {0.52 \, \rm V^2}}{0.0142 \, \rm V^2}\hspace{0.05cm}\rm = 36.65\hspace{0.3cm} \Rightarrow \hspace{0.3cm} 10 \cdot {\rm lg}\hspace{0.1cm}\rho_{\rm V} \hspace{0.15cm}\underline{= {15.64 \, \rm dB}}.$$