Difference between revisions of "Aufgaben:Exercise 2.7Z: DSB-AM and Envelope Demodulator"

Revision as of 21:07, 20 December 2021

Spectrum $R_{\rm TP}(f)$ of the received signal in the equivalent low-pass range

Assume a source signal

$$ q(t) = 2 \,{\rm V} \cdot \cos(2 \pi \cdot 2\,{\rm kHz} \cdot t ) + 2 \,{\rm V} \cdot \sin(2 \pi \cdot 5\,{\rm kHz} \cdot t )\hspace{0.05cm}.$$

This is modulated according to the modulation method "DSB-AM with carrier" and transmitted through an ideal channel. The influence of noise can be disregarded.

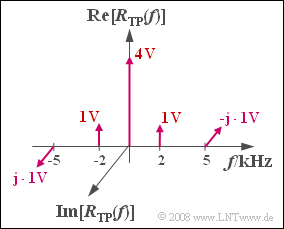
The graph shows the spectrum $R_{\rm TP}(f)$ of the received signal in the equivalent low-pass region, which is composed of Dirac lines at $f = 0$ (originating from the carrier), at $±2\ \rm kHz$ (originating from the cosine component) and at $±5\ \rm kHz$ (originating from the sine component) .

The locus curve is the plot of the equivalent low-pass signal $r_{\rm TP}(t)$ in the complex plane,
where $r_{\rm TP}(t)$ is the Fourier retransform of $R_{\ \rm TP}(f)$ .

Hints:

This exercise belongs to the chapter Envelope Demodulation.
Particular reference is made to the page Description using the equivalent low-pass signal.

Questions

Solution

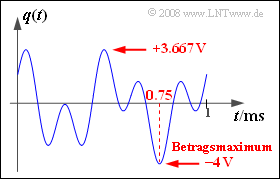
Source signal in the region up to $1\text{ ms}$

(1) The graph shows that the source signal can take on all values between $–4 \ \rm V$ and $+3.667\ \rm V$ annehmen kann.

For example, the maximum magnitude occurs at time $t = t_0 =0.75\ \rm ms$ :

$$q(t = t_0) = 2 \,{\rm V} \cdot \cos(2 \pi \cdot 2\,{\rm kHz} \cdot t_0 ) + 2 \,{\rm V} \cdot \sin(2 \pi \cdot 5\,{\rm kHz} \cdot t_0 )$$

$$\Rightarrow \hspace{0.3cm}q(t = 0.75 \,{\rm ms}) = 2 \,{\rm V} \cdot \cos(3 \pi) + 2 \,{\rm V} \cdot \sin(7.5 \pi)= -4 \,{\rm V}\hspace{0.05cm}.$$

From this, it follows for the maximum magnitude: $q_{\rm max}\hspace{0.15cm}\underline{ = 4 \ \rm V}$.

(2) In the graph on the exercise page, the weight of the Dirac line $f = 0$ indicates the amplitude of the added carrier.

This is $A_{\rm T}\hspace{0.15cm}\underline{ = 4\ \rm V }$.
From this, we get the modulation depth $m = q_{\rm max}/A_{\rm T} \hspace{0.15cm}\underline{ = 1}$.

(3) Answers 2 and 3 are correct:

Since the modulation depth is not greater than $m = 1$ , the envelope demodulator does not cause distortion either.
The main advantage of envelope demodulation is that no frequency and phase synchronization is necessary.
A disadvantage is that a significantly higher power must be applied at the transmitter relative to synchronous demodulation.
When $m = 1$ , this results in three times the transmit power compared to DSB-AM without a carrier.

Equivalent low-pass Signal
in the complex plane

(4) Answers 1 and 3 are correct:

When $ω_2 = 2 π · 2 \ \rm kHz$ and $ω_5 = 2 π · \ \rm 5 kHz$ :

$$ r_{\rm TP}(t) = 4 \,{\rm V} \hspace{-0.05cm}+\hspace{-0.05cm} 1 \,{\rm V} \cdot {\rm e}^{{\rm j} \cdot \hspace{0.03cm}\omega_{\rm 2}\cdot \hspace{0.03cm}t} \hspace{-0.05cm}+\hspace{-0.05cm} 1 \,{\rm V} \cdot {\rm e}^{-{\rm j} \cdot \hspace{0.03cm}\omega_{\rm 2}\cdot \hspace{0.03cm}t} \hspace{-0.05cm}-\hspace{-0.05cm} \hspace{0.15cm}{\rm j} \cdot1 \,{\rm V} \cdot {\rm e}^{{\rm j} \cdot \hspace{0.03cm}\omega_{\rm 5}\cdot \hspace{0.03cm}t} \hspace{-0.05cm}+\hspace{-0.05cm} {\rm j} \cdot1 \,{\rm V} \cdot {\rm e}^{-{\rm j} \cdot \hspace{0.03cm}\omega_{\rm 5}\cdot \hspace{0.03cm}t} \hspace{0.05cm}. \hspace{0.1cm}$$

Thus, in constructing the locus $r_{TP}(t)$ , there are exactly five pointers to consider ⇒ answer 1 is correct. The graph shows a snapshot at time $t = 0$.

The (red) carrier is given by the real pointer of length $4 \ \rm V$ for all time points. In contrast to the pointer diagram (showing the analytic signal), this does not rotate ⇒ Answer 2 is false.
The third statement is similarly correct: The rotating pointers at negative frequencies rotate in mathematically negative direction (clockwise) in contrast to the two pointers with $f > 0$.
The last statement is not true. The larger the frequency $f$ , the faster the associated pointer rotates.

Locus curve for distortionless envelope demodulation

(5) Statements 1 and 2 are correct:

In the example considered, the equivalent low-pass signal can be written as:

$$r_{\rm TP}(t) = q(t) + A_{\rm T} \hspace{0.05cm}.$$

Thus, it is obvious that $r_{\rm TP}(t)$ is always real. Moreover, it follows from subtasks (1) and (2) tht $r_{\rm TP}(t) ≥ 0$.

This means:

Here, the locus curve is a horizontal line on the real plane and always lies in the right half-plane.
These are the two necessary conditions for an envelope demodulator to recover the message signal without distortion.
If one of these conditions is not satisfied, nonlinear distortions arise, not linear ones ⇒ Answer 3 is wrong.

@@ Line 105: / Line 105: @@
 '''(5)'''&nbsp; <u>Statements 1 and 2</u> are correct:
-*In the example considere, the equivalent lowpass signal can be written as:
+*In the example considered, the equivalent low-pass signal can be written as:
 :$$r_{\rm TP}(t) = q(t) + A_{\rm T} \hspace{0.05cm}.$$
 *Thus, it is obvious that &nbsp; $r_{\rm TP}(t)$&nbsp; is always real.&nbsp; Moreover, it follows from subtasks&nbsp; '''(1)'''&nbsp; and&nbsp; '''(2)'''&nbsp; tht &nbsp; $r_{\rm TP}(t) ≥ 0$.

	The locus curve $r_{\rm TP}(t)$ is composed of five pointers.
	The carrier rotates with a rotation speed $ω_{\rm T}$.
	The rotational pointers of the negative frequencies rotate clockwise.
	The pointer for $2 \ \rm kHz$ rotates twice as fast as the one for $5 \ \rm kHz$.

	With the envelope demodulator, distortion-free demodulation is not possible in the example considered.
	One can do without frequency and phase synchronization.
	A smaller transmit power would be needed using a synchronous demodulator.

	A distortionless demodulation is only possible when $r_{\rm TP}(t)$ is real at all times.
	A distortionless demodulation is only possible when $r_{\rm TP}(t)$ does not become negative at any point in time.
	If the first two conditions mentioned are not met, linear distortions will occur.