Difference between revisions of "Aufgaben:Exercise 2.9: Coherence Time"
(Die Seite wurde neu angelegt: „ {{quiz-Header|Buchseite=Mobile Kommunikation/Das GWSSUS–Kanalmodell}} Datei:P_ID2180__Mob_A_2_9.png|right|frame|Doppler–Leistungsdichtespektrum un…“) |
|||
| Line 3: | Line 3: | ||
[[File:P_ID2180__Mob_A_2_9.png|right|frame|Doppler–Leistungsdichtespektrum und Zeit–Korrelationsfunktion]] | [[File:P_ID2180__Mob_A_2_9.png|right|frame|Doppler–Leistungsdichtespektrum und Zeit–Korrelationsfunktion]] | ||
| − | + | In the frequency domain, the influence of Rayleigh fading is described by the [[Mobile_Kommunikation/Statistische_Bindungen_innerhalb_des_Rayleigh-Prozesses#AKF_und_LDS_bei_Rayleigh.E2.80.93Fading| Jakes spectrum]] . If the Rayleigh parameter is $\sigma = \sqrt{0.5}$ the Jakes spectrum is | |
| − | + | $${\it \Phi}_{\rm D}(f_{\rm D}) = \frac{1}{ \pi \cdot f_{\rm D,\hspace{0.05cm}max} \cdot \sqrt{1 - \left (\frac{f_{\rm D}}}{f_{\rm D,\hspace{0.05cm}max}}} \right )^2} } \hspace{0.05cm}.$$ | |
| + | for the Doppler frequency range $|f_{\rm D}| ≤ f_{\rm D, \ max}$: | ||
| + | This function is sketched for $f_{\rm D, \ max} = 50 \ \rm Hz$ (blue curve) and $f_{\rm D, \ max} = 100 \ \rm Hz$ (red curve). | ||
| − | + | The function $\varphi_{\rm Z}(\delta t)$ is the inverse Fourier transform of the Doppler power density spectrum ${\it \Phi}_{\rm D}(f)$: | |
| − | |||
| − | |||
:$$\varphi_{\rm Z}(\Delta t ) = {\rm J}_0(2 \pi \cdot f_{\rm D,\hspace{0.05cm}max} \cdot \Delta t ) \hspace{0.05cm}.$$ | :$$\varphi_{\rm Z}(\Delta t ) = {\rm J}_0(2 \pi \cdot f_{\rm D,\hspace{0.05cm}max} \cdot \Delta t ) \hspace{0.05cm}.$$ | ||
| − | ${\rm J}_0$ | + | ${\rm J}_0$ denotes the <i> zeroth-order Bessel function of the first kind</i>. The correlation function $\varphi_{\rm Z}(\Delta t)$ which is also symmetrical, is drawn below, but for space reasons only the right half. |
| − | + | A characteristic value can be derived from each of these two description functions: | |
| − | * | + | * The <b>Doppler spread</b> $B_{\rm D}$ refers to the Doppler PSD ${\it \Phi}_{\rm D}(f_{\rm D})$ and is equal to the standard deviation $\sigma_{\rm D}$ of the Doppler frequency $f_D$. |
| − | + | Note that the Jakes spectrum is zero-mean, so that the variance $\sigma_{\rm D}^2$ according to Steiner's theorem is equal to the second moment ${\rm E}\big[f_{\rm D}^2\big]$ . The calculation is analogous to the determination of the delay spread $T_{\rm V}$ from the delay PSD ${\it \Phi}_{\rm V}(\tau)$ ⇒ [[Aufgaben:Exercise_2.7:_Coherence_Bandwidth| Exercise 2.7]]. | |
| − | * | + | * The <b>coherence time</b> $T_{\rm D}$ on the other hand, refers to the time correlation function $\varphi_{\rm Z}(\Delta t)$ . |
| − | :: $T_{\rm D}$ | + | :: $T_{\rm D}$ is the value of $\Delta t$– at which the magnitude $|\varphi_{\rm Z}(\Delta t)|$ first drops to half of the maximum $($at $\Delta t = 0)$ . One recognizes the analogy with the determination of the coherence bandwidth $B_{\rm K}$ from the frequency correlation function $\varphi_{\rm F}(\Delta f)$ ⇒ [[Aufgaben:Exercise_2.7:_Coherence_Bandwidth| Exercise 2.7]]. |
| − | '' | + | ''Notes:'' |
| − | * | + | * This task belongs to chapter [[Mobile_Kommunikation/Das_GWSSUS%E2%80%93Kanalmodell| GWSSUS–Kanalmodell]]. |
| − | * | + | * Reference is also made to chapter [[Mobile_Kommunikation/Allgemeine_Beschreibung_zeitvarianter_Systeme| Allgemeine Beschreibung zeitvarianter Systeme]]. |
| − | * | + | * The following undefined integral is given: |
:$$\int \frac{u^2}{\sqrt{1-u^2}} \hspace{0.15cm}{\rm d} u = -\frac{u}{2} \cdot \sqrt{1-u^2} + \frac{1}{2} \cdot {\rm arcsin}\,(u) | :$$\int \frac{u^2}{\sqrt{1-u^2}} \hspace{0.15cm}{\rm d} u = -\frac{u}{2} \cdot \sqrt{1-u^2} + \frac{1}{2} \cdot {\rm arcsin}\,(u) | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| Line 36: | Line 36: | ||
| − | === | + | ===Questionnaire=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Which statements apply to the probability density function (WDF) of the Doppler frequency in the present example? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + The Doppler–WDF is always identical in shape to the Doppler–LDS. |
| − | + | + | + The Doppler–WDF is here identical with the Doppler–LDS. |
| − | - Doppler–WDF | + | - Doppler–WDF and Doppler–LDS differ fundamentally. |
| − | { | + | {Determine the doppler broadenings $B_{\rm D}$. |
|type="{}"} | |type="{}"} | ||
| − | $f_{\rm D, \ max} = 50 \ {\rm Hz} \text | + | $f_{\rm D, \ max} = 50 \ {\rm Hz} \text \ \hspace{0.6cm} B_{\rm D} \ = \ ${ 35.35 3% } $\ \ \rm Hz$ |
| − | $f_{\rm D, \ max} = 100 \ {\rm Hz} \text | + | $f_{\rm D, \ max} = 100 \ {\rm Hz} \text \ \hspace{0.4cm} B_{\rm D} \ = \ ${ 70.7 3% } $\ \ \rm Hz$ |
| − | { | + | {What is the time correlation value for $\Delta t = 5 \ \ \rm ms$? |
|type="{}"} | |type="{}"} | ||
| − | $f_{\rm D, \ max} = 50 \ {\rm Hz} \text | + | $f_{\rm D, \ max} = 50 \ {\rm Hz} \text \ \hspace{0.6cm} \varphi_{\rm Z}(\delta t = 5 \ \rm ms) \ = \ ${ 0.472 3% } |
| − | $f_{\rm D, \ max} = 100 \ {\rm Hz} \text | + | $f_{\rm D, \ max} = 100 \ {\rm Hz} \text \ \hspace{0.4cm} \varphi_{\rm Z}(\delta t = 5 \ \rm ms) \ = \ ${ -0.31415--0.29585 } |
| − | { | + | {What are the correlation durations $T_{\rm D}$ for both parameter sets? |
|type="{}"} | |type="{}"} | ||
| − | $f_{\rm D, \ max} = 50 \ {\rm Hz} \text | + | $f_{\rm D, \ max} = 50 \ {\rm Hz} \text \ \hspace{0.6cm} T_{\rm D} \ = \ ${ 4.84 3% } $\ \ \rm ms$ |
| − | $f_{\rm D, \ max} = 100 \ {\rm Hz} \text | + | $f_{\rm D, \ max} = 100 \ {\rm Hz} \text \ \hspace{0.4cm} T_{\rm D} \ = \ ${ 2.42 3% } $\ \ \rm ms$ |
| − | { | + | {What is the relationship between the Doppler broadening $B_{\rm D}$ and the correlation duration $T_{\rm D}$, based on the Jakes–spectrum? |
|type="()"} | |type="()"} | ||
| − | - $B_{\rm D} \cdot T_{\rm D} \approx 1 | + | - $B_{\rm D} \cdot T_{\rm D} \approx $1, |
- $B_{\rm D} \cdot T_{\rm D} \approx 0.5$, | - $B_{\rm D} \cdot T_{\rm D} \approx 0.5$, | ||
| − | + $B_{\rm D} \cdot T_{\rm D} \approx 0.171 | + | + $B_{\rm D} \cdot T_{\rm D} \approx $0.171. |
</quiz> | </quiz> | ||
| − | === | + | ===Sample solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)'''' <u>Solutions 1 and 2</u> are correct: |
| − | *Doppler | + | *Doppler PDF and Doppler PSD are generally only identical in shape. |
| − | * | + | *But since in the example considered the integral over ${\it \Phi}_{\rm D}(f_{\rm D})$ is equal to $1$, recognizable by the correlation value $\varphi_{\rm Z}(\Delta t = 0) = 1$, even the identity is correct here. |
| − | * | + | *If the Rayleigh parameter $\sigma$ had been chosen differently, this would not apply. |
| − | '''(2)''' | + | '''(2)''' From the axial symmetry of ${\it \Phi}_{\rm D}(f_{\rm D})$ you can see that the mean value $m_{\rm D} = {\rm E}\big [f_{\rm D}\big] = 0$. |
| − | * | + | *The variance of the random variable $f_{\rm D}$ can thus be calculated directly as a square mean value: |
| − | + | $$\sigma_{\rm D}^2 = \int_{-\infty}^{+\infty} f_{\rm D}^2 \cdot {\it \Phi}_{\rm D}(f_{\rm D}) \hspace{0.15cm}{\rm d} f_{\rm D} = \int_{-f_{\rm D,\hspace{0.05cm}max}}}^{+f_{\rm D,\hspace{0.05cm}max}} \frac{f_{\rm D}^2}{ \pi \cdot f_{\rm D,\hspace{0.05cm}max} \cdot \sqrt{1 - \left ({f_{\rm D}}}/{f_{\rm D,\hspace{0.05cm}max}}} \right )^2} } \hspace{0.15cm}{\rm d} f_{\rm D} | |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | * | + | *Using symmetry and with the substitution $u = f_{\rm D}/f_{\rm D, \ max}$ results in |
| − | + | $$\sigma_{\rm D}^2 = \frac{2}{\pi} \cdot f_{\rm D,\hspace{0.05cm}max}^2 \cdot \int_{0}^{1} \frac{u^2}{\sqrt{1-u^2} \hspace{0.15cm}{\rm d} u | |
\hspace{0.05cm}. $$ | \hspace{0.05cm}. $$ | ||
| − | * | + | *With the integral given on the data page you get further: |
| − | + | $$\sigma_{\rm D}^2 \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \frac{2}{\pi} \cdot f_{\rm D,\hspace{0.05cm}max}^2 \cdot \left [ -\frac{u}{2} \cdot \sqrt{1-u^2} + \frac{1}{2} \cdot {\rm arcsin}\,(u) \right ]_0^1 = \frac{2}{\pi} \cdot f_{\rm D,\hspace{0.05cm}max}^2 \cdot \frac{2}{2}\cdot \frac{\pi}{2} = \frac{f_{\rm D,\hspace{0.05cm}max}^2}{2} | |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | * | + | *The Doppler widening is equal to the scatter, i.e. the square root of the variance: |
| − | + | $$B_{\rm D} = \sigma_{\rm D} = \frac{f_{\rm D,\hspace{0.05cm}max}}}{\sqrt{2}}= \left\{ \begin{array}{c} \underline {35.35\,{\rm Hz}}\\\ | |
| − | \underline{70.7\,{\rm Hz}} \end{array} \right.\quad | + | \underline {70.7\,{\rm Hz}} \end{array} \right.\quad |
| − | \begin{array}{*{1}c} {\rm f\ddot{u | + | \begin{array}{*{*{1}c} {\rm f\ddot{u} \hspace{0.15cm}f_{\rm D,\hspace{0.05cm}max} = 50\,{\rm Hz} |
| − | \\ | + | \\ {\rm f\ddot{u} \hspace{0.15cm}f_{\rm D,\hspace{0.05cm}max} = 100\,{\rm Hz} \\ \end{array} |
\hspace{0.05cm}. $$ | \hspace{0.05cm}. $$ | ||
| − | '''(3)''' | + | '''(3)''' With the Bessel values given, one obtains |
| − | * | + | * for the Doppler frequency $f_{\rm D, \ max} = 50 \ \rm Hz$: |
| − | + | $$\varphi_{\rm Z}(\delta t = 5\,{\rm ms}) = {\rm J}_0(2 \pi \cdot 50\,{\rm Hz} \cdot 5\,{\rm ms} ) = {\rm J}_0(\pi/2) \hspace{0.1cm} \underline {= 0.472} \hspace{0.05cm},$$ | |
| − | * | + | * for the Doppler frequency $f_{\rm D, \ max} = 100 \ \rm Hz$: |
| − | + | $$\varphi_{\rm Z}(\delta t = 5\,{\rm ms}) = {\rm J}_0(\pi) \hspace{0.1cm} \underline {= -0.305} \hspace{0.05cm}.$$ | |
| − | '''(4)''' | + | '''(4)''' The correlation duration $T_{\rm D}$ is derived from the time correlation function $\varphi_{\rm Z}(\delta t)$. $T_{\rm D}$ is the $\delta t$–value where $|\varphi_{\rm Z}(\delta t)|$ has decayed to half of its maximum value. It must hold: |
| − | + | $$\varphi_{\rm Z}(\delta t = T_{\rm D}) = {\rm J}_0(2 \pi \cdot f_{\rm D,\hspace{0.05cm}max} \cdot T_{\rm D}) \stackrel {!}{=} 0.5 \hspace{0.3cm} | |
\Rightarrow \hspace{0.3cm} 2 \pi \cdot f_{\rm D,\hspace{0.05cm}max} \cdot T_{\rm D} = 1.52 | \Rightarrow \hspace{0.3cm} 2 \pi \cdot f_{\rm D,\hspace{0.05cm}max} \cdot T_{\rm D} = 1.52 | ||
| − | \hspace{0.3cm} \Rightarrow \hspace{0.3cm} T_{\rm D} = \frac{1.52}{2 \pi f_{\rm D,\hspace{0.05cm}max}} = \frac{0.242}{ f_{\rm D,\hspace{0.05cm}max}}$$ | + | \hspace{0.3cm} \Rightarrow \hspace{0.3cm} T_{\rm D} = \frac{1.52}{2 \pi f_{\rm D,\hspace{0.05cm}max}}} = \frac{0.242}{ f_{\rm D,\hspace{0.05cm}max}}$$ |
| − | + | $$\Rightarrow \hspace{0.3cm} f_{\rm D,\hspace{0.05cm}max} = 50\,{\rm Hz}\text{:} \hspace{-0.1cm}\hspace{0.2cm}\hspace{0.2cm} T_{\rm D} \hspace{0.1cm} \underline {\approx 4.84\,{\rm ms} \hspace{0.05cm},\hspace{0.8cm} f_{\rm D,\hspace{0.05cm}max} = 100\,{\rm Hz}\text{:} \hspace{-0.1cm}\hspace{0.2cm}\hspace{0.2cm} T_{\rm D} \hspace{0.1cm} \underline {\approx 2.42\,{\rm ms} \hspace{0.05cm}. $$ | |
| − | '''(5)''' In | + | '''(5)''' In the subtasks '''(2)''' and '''(4)''' we received |
| − | + | $$B_{\rm D} = \frac{ f_{\rm D,\hspace{0.05cm}max}}}}{\sqrt{2}}\hspace{0.05cm}, \hspace{0.2cm} T_{\rm D} = \frac{1.52}{2 \pi f_{\rm D,\hspace{0.05cm}max}}\hspace{0.3cm} | |
| − | \Rightarrow \hspace{0.3cm} B_{\rm D} \cdot T_{\rm D} = | + | \Rightarrow \hspace{0.3cm} B_{\rm D} \cdot T_{\rm D} = \frac{1.52}{\sqrt{2} \cdot 2 \pi } \hspace{0.1cm}\underline {\approx 0.171}\hspace{0.05cm}.$$ |
| − | + | Correct is therefore the <u>last proposed solution</u>. | |
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | |||
[[Category:Exercises for Mobile Communications|^2.3 The GWSSUS Channel Model^]] | [[Category:Exercises for Mobile Communications|^2.3 The GWSSUS Channel Model^]] | ||
Revision as of 10:51, 23 April 2020
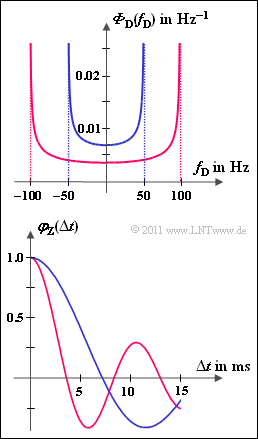
In the frequency domain, the influence of Rayleigh fading is described by the Jakes spectrum . If the Rayleigh parameter is $\sigma = \sqrt{0.5}$ the Jakes spectrum is $${\it \Phi}_{\rm D}(f_{\rm D}) = \frac{1}{ \pi \cdot f_{\rm D,\hspace{0.05cm}max} \cdot \sqrt{1 - \left (\frac{f_{\rm D}}}{f_{\rm D,\hspace{0.05cm}max}}} \right )^2} } \hspace{0.05cm}.$$ for the Doppler frequency range $|f_{\rm D}| ≤ f_{\rm D, \ max}$: This function is sketched for $f_{\rm D, \ max} = 50 \ \rm Hz$ (blue curve) and $f_{\rm D, \ max} = 100 \ \rm Hz$ (red curve).
The function $\varphi_{\rm Z}(\delta t)$ is the inverse Fourier transform of the Doppler power density spectrum ${\it \Phi}_{\rm D}(f)$:
- $$\varphi_{\rm Z}(\Delta t ) = {\rm J}_0(2 \pi \cdot f_{\rm D,\hspace{0.05cm}max} \cdot \Delta t ) \hspace{0.05cm}.$$
${\rm J}_0$ denotes the zeroth-order Bessel function of the first kind. The correlation function $\varphi_{\rm Z}(\Delta t)$ which is also symmetrical, is drawn below, but for space reasons only the right half.
A characteristic value can be derived from each of these two description functions:
- The Doppler spread $B_{\rm D}$ refers to the Doppler PSD ${\it \Phi}_{\rm D}(f_{\rm D})$ and is equal to the standard deviation $\sigma_{\rm D}$ of the Doppler frequency $f_D$.
Note that the Jakes spectrum is zero-mean, so that the variance $\sigma_{\rm D}^2$ according to Steiner's theorem is equal to the second moment ${\rm E}\big[f_{\rm D}^2\big]$ . The calculation is analogous to the determination of the delay spread $T_{\rm V}$ from the delay PSD ${\it \Phi}_{\rm V}(\tau)$ ⇒ Exercise 2.7.
- The coherence time $T_{\rm D}$ on the other hand, refers to the time correlation function $\varphi_{\rm Z}(\Delta t)$ .
- $T_{\rm D}$ is the value of $\Delta t$– at which the magnitude $|\varphi_{\rm Z}(\Delta t)|$ first drops to half of the maximum $($at $\Delta t = 0)$ . One recognizes the analogy with the determination of the coherence bandwidth $B_{\rm K}$ from the frequency correlation function $\varphi_{\rm F}(\Delta f)$ ⇒ Exercise 2.7.
Notes:
- This task belongs to chapter GWSSUS–Kanalmodell.
- Reference is also made to chapter Allgemeine Beschreibung zeitvarianter Systeme.
- The following undefined integral is given:
- $$\int \frac{u^2}{\sqrt{1-u^2}} \hspace{0.15cm}{\rm d} u = -\frac{u}{2} \cdot \sqrt{1-u^2} + \frac{1}{2} \cdot {\rm arcsin}\,(u) \hspace{0.05cm}.$$
- Abschließend noch einige Werte für die Besselfunktion nullter Ordnung $({\rm J}_0)$:
- $${\rm J}_0(\pi/2) = 0.472\hspace{0.05cm},\hspace{0.4cm}{\rm J}_0(1.52) = 0.500\hspace{0.05cm},\hspace{0.4cm}{\rm J}_0(\pi) = -0.305\hspace{0.05cm},\hspace{0.4cm} {\rm J}_0(2\pi) = 0.221 \hspace{0.05cm}.$$
Questionnaire
Sample solution
- Doppler PDF and Doppler PSD are generally only identical in shape.
- But since in the example considered the integral over ${\it \Phi}_{\rm D}(f_{\rm D})$ is equal to $1$, recognizable by the correlation value $\varphi_{\rm Z}(\Delta t = 0) = 1$, even the identity is correct here.
- If the Rayleigh parameter $\sigma$ had been chosen differently, this would not apply.
(2) From the axial symmetry of ${\it \Phi}_{\rm D}(f_{\rm D})$ you can see that the mean value $m_{\rm D} = {\rm E}\big [f_{\rm D}\big] = 0$.
- The variance of the random variable $f_{\rm D}$ can thus be calculated directly as a square mean value:
$$\sigma_{\rm D}^2 = \int_{-\infty}^{+\infty} f_{\rm D}^2 \cdot {\it \Phi}_{\rm D}(f_{\rm D}) \hspace{0.15cm}{\rm d} f_{\rm D} = \int_{-f_{\rm D,\hspace{0.05cm}max}}}^{+f_{\rm D,\hspace{0.05cm}max}} \frac{f_{\rm D}^2}{ \pi \cdot f_{\rm D,\hspace{0.05cm}max} \cdot \sqrt{1 - \left ({f_{\rm D}}}/{f_{\rm D,\hspace{0.05cm}max}}} \right )^2} } \hspace{0.15cm}{\rm d} f_{\rm D} \hspace{0.05cm}.$$
- Using symmetry and with the substitution $u = f_{\rm D}/f_{\rm D, \ max}$ results in
$$\sigma_{\rm D}^2 = \frac{2}{\pi} \cdot f_{\rm D,\hspace{0.05cm}max}^2 \cdot \int_{0}^{1} \frac{u^2}{\sqrt{1-u^2} \hspace{0.15cm}{\rm d} u \hspace{0.05cm}. $$
- With the integral given on the data page you get further:
$$\sigma_{\rm D}^2 \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \frac{2}{\pi} \cdot f_{\rm D,\hspace{0.05cm}max}^2 \cdot \left [ -\frac{u}{2} \cdot \sqrt{1-u^2} + \frac{1}{2} \cdot {\rm arcsin}\,(u) \right ]_0^1 = \frac{2}{\pi} \cdot f_{\rm D,\hspace{0.05cm}max}^2 \cdot \frac{2}{2}\cdot \frac{\pi}{2} = \frac{f_{\rm D,\hspace{0.05cm}max}^2}{2} \hspace{0.05cm}.$$
- The Doppler widening is equal to the scatter, i.e. the square root of the variance:
$$B_{\rm D} = \sigma_{\rm D} = \frac{f_{\rm D,\hspace{0.05cm}max}}}{\sqrt{2}}= \left\{ \begin{array}{c} \underline {35.35\,{\rm Hz}}\\\ \underline {70.7\,{\rm Hz}} \end{array} \right.\quad \begin{array}{*{*{1}c} {\rm f\ddot{u} \hspace{0.15cm}f_{\rm D,\hspace{0.05cm}max} = 50\,{\rm Hz} \\ {\rm f\ddot{u} \hspace{0.15cm}f_{\rm D,\hspace{0.05cm}max} = 100\,{\rm Hz} \\ \end{array} \hspace{0.05cm}. $$
(3) With the Bessel values given, one obtains
- for the Doppler frequency $f_{\rm D, \ max} = 50 \ \rm Hz$:
$$\varphi_{\rm Z}(\delta t = 5\,{\rm ms}) = {\rm J}_0(2 \pi \cdot 50\,{\rm Hz} \cdot 5\,{\rm ms} ) = {\rm J}_0(\pi/2) \hspace{0.1cm} \underline {= 0.472} \hspace{0.05cm},$$
- for the Doppler frequency $f_{\rm D, \ max} = 100 \ \rm Hz$:
$$\varphi_{\rm Z}(\delta t = 5\,{\rm ms}) = {\rm J}_0(\pi) \hspace{0.1cm} \underline {= -0.305} \hspace{0.05cm}.$$
(4) The correlation duration $T_{\rm D}$ is derived from the time correlation function $\varphi_{\rm Z}(\delta t)$. $T_{\rm D}$ is the $\delta t$–value where $|\varphi_{\rm Z}(\delta t)|$ has decayed to half of its maximum value. It must hold: $$\varphi_{\rm Z}(\delta t = T_{\rm D}) = {\rm J}_0(2 \pi \cdot f_{\rm D,\hspace{0.05cm}max} \cdot T_{\rm D}) \stackrel {!}{=} 0.5 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} 2 \pi \cdot f_{\rm D,\hspace{0.05cm}max} \cdot T_{\rm D} = 1.52 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} T_{\rm D} = \frac{1.52}{2 \pi f_{\rm D,\hspace{0.05cm}max}}} = \frac{0.242}{ f_{\rm D,\hspace{0.05cm}max}}$$ $$\Rightarrow \hspace{0.3cm} f_{\rm D,\hspace{0.05cm}max} = 50\,{\rm Hz}\text{:} \hspace{-0.1cm}\hspace{0.2cm}\hspace{0.2cm} T_{\rm D} \hspace{0.1cm} \underline {\approx 4.84\,{\rm ms} \hspace{0.05cm},\hspace{0.8cm} f_{\rm D,\hspace{0.05cm}max} = 100\,{\rm Hz}\text{:} \hspace{-0.1cm}\hspace{0.2cm}\hspace{0.2cm} T_{\rm D} \hspace{0.1cm} \underline {\approx 2.42\,{\rm ms} \hspace{0.05cm}. $$
(5) In the subtasks (2) and (4) we received
$$B_{\rm D} = \frac{ f_{\rm D,\hspace{0.05cm}max}}}}{\sqrt{2}}\hspace{0.05cm}, \hspace{0.2cm} T_{\rm D} = \frac{1.52}{2 \pi f_{\rm D,\hspace{0.05cm}max}}\hspace{0.3cm}
\Rightarrow \hspace{0.3cm} B_{\rm D} \cdot T_{\rm D} = \frac{1.52}{\sqrt{2} \cdot 2 \pi } \hspace{0.1cm}\underline {\approx 0.171}\hspace{0.05cm}.$$
Correct is therefore the last proposed solution.