Difference between revisions of "Aufgaben:Exercise 3.09: Correlation Receiver for Unipolar Signaling"
| (28 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Digital_Signal_Transmission/Optimal_Receiver_Strategies}} |
| − | [[File:P_ID1464__Dig_A_3_9.png|right|frame| | + | [[File:P_ID1464__Dig_A_3_9.png|right|frame|Example correlation values]] |
| − | + | The joint decision of $N = 3$ binary symbols ("bits") by means of the correlation receiver is considered. | |
| + | |||
| + | The $M = 8$ possible source symbol sequences $Q_i$ all have the same probability and they are defined by the following unipolar amplitude coefficients: | ||
:$$Q_0 = 000, \hspace{0.15cm}Q_1 = 001,\hspace{0.15cm}Q_2 = 010,\hspace{0.15cm}Q_3 = 011 | :$$Q_0 = 000, \hspace{0.15cm}Q_1 = 001,\hspace{0.15cm}Q_2 = 010,\hspace{0.15cm}Q_3 = 011 | ||
| − | \hspace{0.05cm}, | + | \hspace{0.05cm},\hspace{0.15cm} |
| − | + | Q_4 = 100, \hspace{0.15cm}Q_5 = 101,\hspace{0.15cm}Q_6 = 110,\hspace{0.15cm}Q_7 = 111 | |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | Further applies: | |
| + | *The possible transmitted signals $s_i(t)$ – each with duration $3T$ – are all rectangular with the exception of $s_0(t) \equiv 0$. | ||
| + | |||
| + | *The signals $s_1(t)$, $s_2(t)$ and $s_4(t)$ with only one "$1$" each have the signal energy $E_{\rm B}$ (stands for "energy per bit"), while for example the energy of $s_7(t)=3E_{\rm B}$. | ||
| + | |||
| − | + | The correlation receiver forms from the noisy received signal $r(t) = s(t) + n(t)$ a total of $2^3 = 8$ decision variables (metrics) | |
| − | :$$W_i = I_i - {E_i}/{2 }\hspace{0.3cm}{\rm | + | :$$W_i = I_i - {E_i}/{2 }\hspace{0.3cm}{\rm with}\hspace{0.3cm} |
I_i =\int_{0}^{3T} r(t) \cdot s_i(t) \,{\rm d} t | I_i =\int_{0}^{3T} r(t) \cdot s_i(t) \,{\rm d} t | ||
| − | \hspace{0.3cm}( i = 0, ... , 7)$$ | + | \hspace{0.3cm}( i = 0,\text{...} , 7)$$ |
| + | |||
| + | and sets the sink symbol sequence $V = Q_j$, if $W_j$ is larger than all other $W_{i \ne j}$. Thus, it makes an optimal decision in the sense of "maximum likelihood". | ||
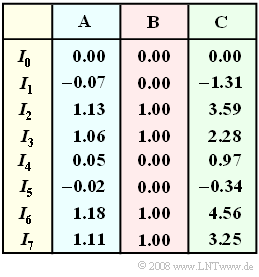
| − | + | In the table, the (uncorrected) correlation values $I_0, \ \text{...} \ , I_7$ for three different systems differing in terms of noise $n(t)$ and labeled $\rm A$, $\rm B$ or $\rm C$. | |
| + | *One of these columns stands for "no noise", | ||
| + | *one for "minor noise", and | ||
| + | *another one for "strong noise". | ||
| − | |||
| − | |||
| − | |||
| − | |||
| + | Note: | ||
| + | *The exercise belongs to the chapter [[Digital_Signal_Transmission/Optimal_Receiver_Strategies|"Optimal Receiver Strategies"]]. | ||
| + | |||
| + | *The same source symbol sequence was always sent to determine the metrics for the three system variants. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ===Question=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {For which system is there "no noise" ⇒ $n(t)=0$? At |
| − | |type=" | + | |type="()"} |
| − | - | + | - $\rm System \ A$, |
| − | + | + | + $\rm System \ B$, |
| + | - $\rm System \ C$. | ||
| + | |||
| + | {Which source symbol sequence $Q_k ∈ {Q_0, \ \text{...} \ , Q_7}$ was actually sent? | ||
| + | |type="{}"} | ||
| + | $k \ = \ $ { 2 } | ||
| + | {Which decision value $W_j$ is largest for system $\rm A$? | ||
| + | |type="{}"} | ||
| + | ${\rm System \ A} \text{:} \hspace{0.2cm} j \ = \ $ { 2 } | ||
| − | { | + | {Which decision value $W_j$ is largest for system $\rm C$? |
|type="{}"} | |type="{}"} | ||
| − | $\ | + | ${\rm System \ C} \text{:} \hspace{0.2cm} j \ = \ $ { 6 } |
| + | |||
| + | {For which system do the largest noise occur? At | ||
| + | |type="()"} | ||
| + | - $\rm System \ A$, | ||
| + | - $\rm System \ B$, | ||
| + | + $\rm System \ C$. | ||
| + | |||
| + | {Which statements are valid under the assumption that $Q_2$ was sent and the correlation receiver normally chooses $Q_2$ as well? | ||
| + | |type="[]"} | ||
| + | + The difference between $W_2$ and the next largest value $W_{i \ne 2}$ is smaller the stronger the noise is. | ||
| + | - When falsification occurs, the receiver is most likely to decide in favor of the symbol sequence $Q_6$. | ||
| + | + The probabilities for erroneous decisions in favor of $Q_0$, $Q_3$ and $Q_6$, respectively, are equal. | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' <u>Solution 2</u> is correct: |
| − | '''(2)''' | + | *For system $\rm B$, metrics "$0$" occur four times and metrics "$1$" occur four times. |
| − | '''(3)''' | + | *This points to $n(t) = 0$, otherwise – as in systems $\rm A$ and $\rm C$ – all $I_i$ would have to differ. |
| − | '''(4)''' | + | |
| − | '''(5)''' | + | |
| − | '''(6)''' | + | '''(2)''' For system $\rm B$, the decision values $W_i = I_i \ - E_i/2$, each normalized to $E_{\rm B}$, are as follows: |
| + | :$$W_0 = 0 - 0 = 0, \hspace{0.2cm}W_1 = 0 - 0.5 = -0.5 | ||
| + | \hspace{0.05cm},$$ | ||
| + | :$$W_2 = 1 - 0.5 = 0.5, \hspace{0.2cm}W_3 = 1 - 1 = 0 | ||
| + | \hspace{0.05cm},$$ | ||
| + | :$$W_4 = 0 - 0.5 = -0.5, \hspace{0.2cm}W_5 = 0 - 1 = -1 | ||
| + | \hspace{0.05cm}.$$ | ||
| + | :$$W_6 = 1 - 1 = 0, \hspace{0.2cm}W_7 = 1 - 1.5 = | ||
| + | -0.5 | ||
| + | \hspace{0.05cm}.$$ | ||
| + | |||
| + | *The maximum value $W_2 = 0.5$ ⇒ $i = 2$. | ||
| + | *Thus, the correlation receiver decides to use $V = Q_2$. | ||
| + | *Since there is no noise, $Q_2 =$ "$\rm 010$" was indeed also sent ⇒ $\underline { k= 2}$. | ||
| + | |||
| + | |||
| + | '''(3)''' For the decision values of system $\rm A$ holds: | ||
| + | :$$W_0 = 0.00 - 0.00 = 0.00, \hspace{0.2cm}W_1 = -0.07 - 0.50 = -0.57, $$ | ||
| + | :$$W_2 = 1.13 - 0.50 = 0.63, \hspace{0.2cm}W_3 = 1.06 - 1.00 = 0.06 \hspace{0.05cm},$$ | ||
| + | :$$W_4 = 0.05 - 0.50 = -0.45, \hspace{0.2cm}W_5 = -0.02 - 1.00 = -1.02\hspace{0.05cm},$$ | ||
| + | :$$W_6 = 1.18 - 1.00 = 0.18, \hspace{0.2cm}W_7 = 1.11 - 1.50 = -0.39 \hspace{0.05cm}.$$ | ||
| + | |||
| + | *The maximum is = $W_j = W_2$ ⇒ $\underline { j= 2}$. | ||
| + | *This means that the correlation receiver also makes the correct decision $V = Q_2$ for system $\rm A$. | ||
| + | *However, without the correction term $(– E_i/2)$, the receiver would have made the wrong decision $V = Q_6$. | ||
| + | |||
| + | |||
| + | '''(4)''' The correlation receiver $\rm C$ has to compare the following values: | ||
| + | :$$W_0 = 0.00 - 0.00 = 0.00, \hspace{0.2cm}W_1 = -1.31 - 0.50 = | ||
| + | -1.81 | ||
| + | \hspace{0.05cm},$$ | ||
| + | :$$W_2 = 3.59 - 0.50 = 3.09, \hspace{0.2cm}W_3 = 2.28 - 1.00 = | ||
| + | 1.28 | ||
| + | \hspace{0.05cm},$$ | ||
| + | :$$W_4 = 0.97 - 0.50 = 0.47, \hspace{0.2cm}W_5 = -0.34 - 1.00 = | ||
| + | -1.34 | ||
| + | \hspace{0.05cm},$$ | ||
| + | :$$W_6 = 4.56 - 1.00 = 3.56, \hspace{0.2cm}W_7 = 3.25 - 1.50 = | ||
| + | 1.75 | ||
| + | \hspace{0.05cm}.$$ | ||
| + | |||
| + | The maximization here gives $\underline {j = 6}$ ⇒ $V = Q_6$. | ||
| + | *But since $Q_2$ was sent, the correlation receiver decides wrong here. | ||
| + | *The noise is too strong. | ||
| + | |||
| + | |||
| + | |||
| + | '''(5)''' <u>Solution 3</u> is correct: | ||
| + | *The noise is greatest for system $\rm C$ and is even so great for the current received values that the correlation receiver makes an incorrect decision. | ||
| + | |||
| + | |||
| + | |||
| + | '''(6)''' <u>Statements 1 and 3</u> are correct: | ||
| + | *In the error-free case $($system $\rm B)$, the difference between $W_2 = 0.5$ and the next largest values $W_0 = W_3 = W_6 = 0$ is equal to $D_{\hspace{0.02cm}\rm min} =0.5$ in each case. | ||
| + | |||
| + | *In system $\rm A$ (light noise), the difference between $W_2 = 0.63$ and the next largest value $W_6 = 0.18$ is still $D_{\hspace{0.02cm}\rm min} = 0.45$. | ||
| + | |||
| + | *If the noise power is increased by factor $50$, the correlation receiver still decides correctly, but then the minimum difference $D_{\hspace{0.02cm}\rm min} = 0.16$ is significantly smaller. | ||
| + | |||
| + | *For system $\rm C$, where the correlation receiver is overcharged ⇒ subtask '''(4)''', a noise power larger by a factor of $400$ compared to system $\rm A$ was used as a basis. | ||
| + | |||
| + | *If the correlation receiver decides the transmitted sequence $Q_2$ incorrectly, a falsification to the sequences $Q_0$, $Q_3$ resp. $Q_6$ is most likely, <br>since all these three sequences differ from $Q_2$ only in one bit each. | ||
| + | |||
| + | *The fact that $W_6$ is always larger than $W_0$ or $W_3$ in the described simulation is "coincidence" and should not be overinterpreted. | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category: | + | [[Category:Digital Signal Transmission: Exercises|^3.7 Optimal Receiver Strategies^]] |
Latest revision as of 17:55, 30 June 2022
The joint decision of $N = 3$ binary symbols ("bits") by means of the correlation receiver is considered.
The $M = 8$ possible source symbol sequences $Q_i$ all have the same probability and they are defined by the following unipolar amplitude coefficients:
- $$Q_0 = 000, \hspace{0.15cm}Q_1 = 001,\hspace{0.15cm}Q_2 = 010,\hspace{0.15cm}Q_3 = 011 \hspace{0.05cm},\hspace{0.15cm} Q_4 = 100, \hspace{0.15cm}Q_5 = 101,\hspace{0.15cm}Q_6 = 110,\hspace{0.15cm}Q_7 = 111 \hspace{0.05cm}.$$
Further applies:
- The possible transmitted signals $s_i(t)$ – each with duration $3T$ – are all rectangular with the exception of $s_0(t) \equiv 0$.
- The signals $s_1(t)$, $s_2(t)$ and $s_4(t)$ with only one "$1$" each have the signal energy $E_{\rm B}$ (stands for "energy per bit"), while for example the energy of $s_7(t)=3E_{\rm B}$.
The correlation receiver forms from the noisy received signal $r(t) = s(t) + n(t)$ a total of $2^3 = 8$ decision variables (metrics)
- $$W_i = I_i - {E_i}/{2 }\hspace{0.3cm}{\rm with}\hspace{0.3cm} I_i =\int_{0}^{3T} r(t) \cdot s_i(t) \,{\rm d} t \hspace{0.3cm}( i = 0,\text{...} , 7)$$
and sets the sink symbol sequence $V = Q_j$, if $W_j$ is larger than all other $W_{i \ne j}$. Thus, it makes an optimal decision in the sense of "maximum likelihood".
In the table, the (uncorrected) correlation values $I_0, \ \text{...} \ , I_7$ for three different systems differing in terms of noise $n(t)$ and labeled $\rm A$, $\rm B$ or $\rm C$.
- One of these columns stands for "no noise",
- one for "minor noise", and
- another one for "strong noise".
Note:
- The exercise belongs to the chapter "Optimal Receiver Strategies".
- The same source symbol sequence was always sent to determine the metrics for the three system variants.
Question
Solution
- For system $\rm B$, metrics "$0$" occur four times and metrics "$1$" occur four times.
- This points to $n(t) = 0$, otherwise – as in systems $\rm A$ and $\rm C$ – all $I_i$ would have to differ.
(2) For system $\rm B$, the decision values $W_i = I_i \ - E_i/2$, each normalized to $E_{\rm B}$, are as follows:
- $$W_0 = 0 - 0 = 0, \hspace{0.2cm}W_1 = 0 - 0.5 = -0.5 \hspace{0.05cm},$$
- $$W_2 = 1 - 0.5 = 0.5, \hspace{0.2cm}W_3 = 1 - 1 = 0 \hspace{0.05cm},$$
- $$W_4 = 0 - 0.5 = -0.5, \hspace{0.2cm}W_5 = 0 - 1 = -1 \hspace{0.05cm}.$$
- $$W_6 = 1 - 1 = 0, \hspace{0.2cm}W_7 = 1 - 1.5 = -0.5 \hspace{0.05cm}.$$
- The maximum value $W_2 = 0.5$ ⇒ $i = 2$.
- Thus, the correlation receiver decides to use $V = Q_2$.
- Since there is no noise, $Q_2 =$ "$\rm 010$" was indeed also sent ⇒ $\underline { k= 2}$.
(3) For the decision values of system $\rm A$ holds:
- $$W_0 = 0.00 - 0.00 = 0.00, \hspace{0.2cm}W_1 = -0.07 - 0.50 = -0.57, $$
- $$W_2 = 1.13 - 0.50 = 0.63, \hspace{0.2cm}W_3 = 1.06 - 1.00 = 0.06 \hspace{0.05cm},$$
- $$W_4 = 0.05 - 0.50 = -0.45, \hspace{0.2cm}W_5 = -0.02 - 1.00 = -1.02\hspace{0.05cm},$$
- $$W_6 = 1.18 - 1.00 = 0.18, \hspace{0.2cm}W_7 = 1.11 - 1.50 = -0.39 \hspace{0.05cm}.$$
- The maximum is = $W_j = W_2$ ⇒ $\underline { j= 2}$.
- This means that the correlation receiver also makes the correct decision $V = Q_2$ for system $\rm A$.
- However, without the correction term $(– E_i/2)$, the receiver would have made the wrong decision $V = Q_6$.
(4) The correlation receiver $\rm C$ has to compare the following values:
- $$W_0 = 0.00 - 0.00 = 0.00, \hspace{0.2cm}W_1 = -1.31 - 0.50 = -1.81 \hspace{0.05cm},$$
- $$W_2 = 3.59 - 0.50 = 3.09, \hspace{0.2cm}W_3 = 2.28 - 1.00 = 1.28 \hspace{0.05cm},$$
- $$W_4 = 0.97 - 0.50 = 0.47, \hspace{0.2cm}W_5 = -0.34 - 1.00 = -1.34 \hspace{0.05cm},$$
- $$W_6 = 4.56 - 1.00 = 3.56, \hspace{0.2cm}W_7 = 3.25 - 1.50 = 1.75 \hspace{0.05cm}.$$
The maximization here gives $\underline {j = 6}$ ⇒ $V = Q_6$.
- But since $Q_2$ was sent, the correlation receiver decides wrong here.
- The noise is too strong.
(5) Solution 3 is correct:
- The noise is greatest for system $\rm C$ and is even so great for the current received values that the correlation receiver makes an incorrect decision.
(6) Statements 1 and 3 are correct:
- In the error-free case $($system $\rm B)$, the difference between $W_2 = 0.5$ and the next largest values $W_0 = W_3 = W_6 = 0$ is equal to $D_{\hspace{0.02cm}\rm min} =0.5$ in each case.
- In system $\rm A$ (light noise), the difference between $W_2 = 0.63$ and the next largest value $W_6 = 0.18$ is still $D_{\hspace{0.02cm}\rm min} = 0.45$.
- If the noise power is increased by factor $50$, the correlation receiver still decides correctly, but then the minimum difference $D_{\hspace{0.02cm}\rm min} = 0.16$ is significantly smaller.
- For system $\rm C$, where the correlation receiver is overcharged ⇒ subtask (4), a noise power larger by a factor of $400$ compared to system $\rm A$ was used as a basis.
- If the correlation receiver decides the transmitted sequence $Q_2$ incorrectly, a falsification to the sequences $Q_0$, $Q_3$ resp. $Q_6$ is most likely,
since all these three sequences differ from $Q_2$ only in one bit each.
- The fact that $W_6$ is always larger than $W_0$ or $W_3$ in the described simulation is "coincidence" and should not be overinterpreted.