Difference between revisions of "Aufgaben:Exercise 3.10: Mutual Information at the BSC"
From LNTwww
m (Guenter moved page Aufgabe 3.10: Transinformation beim BSC to Exercise 3.10: Mutual Information at the BSC) |
|||
| Line 2: | Line 2: | ||
}} | }} | ||
| − | [[File:P_ID2787__Inf_A_3_9.png|right|frame| | + | [[File:P_ID2787__Inf_A_3_9.png|right|frame|BSC Model Considered]] |
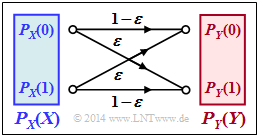
| − | + | We consider the [[Channel_Coding/Kanalmodelle_und_EntscheiderstrukturenBinary Symmetric Channel|Binary Symmetric Channel]] $\rm (BSC)$. The parameter values are valid for the whole exercise: | |
| − | * | + | * Probability of falsification: $\varepsilon = 0.1$, |
| − | * | + | * Probability for $0$: $p_0 = 0.2$, |
| − | * | + | * Probability for $1$: $p_1 = 0.8$. |
| − | + | Thus the probability function of the source is: $P_X(X)= (0.2 , \ 0.8)$ and for the source entropy applies: | |
:$$H(X) = p_0 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{p_0} + p_1\cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{p_1} = H_{\rm bin}(0.2)={ 0.7219\,{\rm bit}} \hspace{0.05cm}.$$ | :$$H(X) = p_0 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{p_0} + p_1\cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{p_1} = H_{\rm bin}(0.2)={ 0.7219\,{\rm bit}} \hspace{0.05cm}.$$ | ||
| − | + | The task is to determine: | |
| − | * | + | * the probability function of the sink: |
:$$P_Y(Y) = (\hspace{0.05cm}P_Y(0)\hspace{0.05cm}, \ \hspace{0.05cm} P_Y(1)\hspace{0.05cm}) | :$$P_Y(Y) = (\hspace{0.05cm}P_Y(0)\hspace{0.05cm}, \ \hspace{0.05cm} P_Y(1)\hspace{0.05cm}) | ||
\hspace{0.05cm},$$ | \hspace{0.05cm},$$ | ||
| − | * | + | * the joint probability function: |
:$$P_{XY}(X, Y) = \begin{pmatrix} | :$$P_{XY}(X, Y) = \begin{pmatrix} | ||
p_{00} & p_{01}\\ | p_{00} & p_{01}\\ | ||
p_{10} & p_{11} | p_{10} & p_{11} | ||
\end{pmatrix} \hspace{0.05cm},$$ | \end{pmatrix} \hspace{0.05cm},$$ | ||
| − | * | + | * the mutual information: |
:$$I(X;Y) = {\rm E} \hspace{-0.08cm}\left [ \hspace{0.02cm}{\rm log}_2 \hspace{0.1cm} \frac{P_{XY}(X, Y)} | :$$I(X;Y) = {\rm E} \hspace{-0.08cm}\left [ \hspace{0.02cm}{\rm log}_2 \hspace{0.1cm} \frac{P_{XY}(X, Y)} | ||
{P_{X}(X) \cdot P_{Y}(Y) }\right ] \hspace{0.05cm},$$ | {P_{X}(X) \cdot P_{Y}(Y) }\right ] \hspace{0.05cm},$$ | ||
| − | * | + | *the equivocation: |
:$$H(X \hspace{-0.1cm}\mid \hspace{-0.1cm} Y) = {\rm E} \hspace{0.02cm} \big [ \hspace{0.02cm} {\rm log}_2 \hspace{0.1cm} \frac{1}{P_{\hspace{0.03cm}X \mid \hspace{0.03cm} Y} (X \hspace{-0.05cm}\mid \hspace{-0.05cm} Y)} \big ] \hspace{0.05cm},$$ | :$$H(X \hspace{-0.1cm}\mid \hspace{-0.1cm} Y) = {\rm E} \hspace{0.02cm} \big [ \hspace{0.02cm} {\rm log}_2 \hspace{0.1cm} \frac{1}{P_{\hspace{0.03cm}X \mid \hspace{0.03cm} Y} (X \hspace{-0.05cm}\mid \hspace{-0.05cm} Y)} \big ] \hspace{0.05cm},$$ | ||
| − | * | + | *the irrelevance: |
:$$H(Y \hspace{-0.1cm}\mid \hspace{-0.1cm} X) = {\rm E} \hspace{0.02cm} \big [ \hspace{0.02cm} {\rm log}_2 \hspace{0.1cm} \frac{1}{P_{\hspace{0.03cm}Y \mid \hspace{0.03cm} X} (Y \hspace{-0.05cm}\mid \hspace{-0.05cm} X)} \big ] \hspace{0.05cm}.$$ | :$$H(Y \hspace{-0.1cm}\mid \hspace{-0.1cm} X) = {\rm E} \hspace{0.02cm} \big [ \hspace{0.02cm} {\rm log}_2 \hspace{0.1cm} \frac{1}{P_{\hspace{0.03cm}Y \mid \hspace{0.03cm} X} (Y \hspace{-0.05cm}\mid \hspace{-0.05cm} X)} \big ] \hspace{0.05cm}.$$ | ||
| Line 35: | Line 35: | ||
| − | + | Hints: | |
| − | * | + | *The task belongs to the chapter [[Information_Theory/Anwendung_auf_die_Digitalsignalübertragung|Application to Digital Signal Transmission]]. |
| − | *Bezug genommen wird insbesondere auf die Seite [[Information_Theory/Anwendung_auf_die_Digitalsignalübertragung# | + | *Bezug genommen wird insbesondere auf die Seite [[Information_Theory/Anwendung_auf_die_Digitalsignalübertragung#Calculation_of_the_mutual_information_for_the_binary_channel|Mutual information calculation for the binary channel]]. |
| − | *In | + | *In [[Aufgaben:Aufgabe_3.10Z:_BSC–Kanalkapazität|task 3.10Z]] the channel capacity $C_{\rm BSC }$ of the BSC model is calculated. |
| − | * | + | *This results as the maximum mutual information $I(X;\ Y)$ by maximisation with respect to the probabilities $p_0$ or $p_1 = 1 - p_0$. |
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Calculate the joint probabilities $P_{ XY }(X, Y)$ |
|type="{}"} | |type="{}"} | ||
$P_{ XY }(0, 0) \ = \ $ { 0.18 3% } | $P_{ XY }(0, 0) \ = \ $ { 0.18 3% } | ||
| Line 54: | Line 54: | ||
$P_{ XY }(1, 1) \ = \ $ { 0.72 3% } | $P_{ XY }(1, 1) \ = \ $ { 0.72 3% } | ||
| − | { | + | {What is the probability function $P_Y(Y)$ of the sink? |
|type="{}"} | |type="{}"} | ||
$P_Y(0)\ = \ $ { 0.26 3% } | $P_Y(0)\ = \ $ { 0.26 3% } | ||
$P_Y(1) \ = \ $ { 0.74 3% } | $P_Y(1) \ = \ $ { 0.74 3% } | ||
| − | { | + | {What is the value of the mutual information $I(X;\ |
Y)$? | Y)$? | ||
|type="{}"} | |type="{}"} | ||
$I(X; Y)\ = \ $ { 0.3578 3% } $\ \rm bit$ | $I(X; Y)\ = \ $ { 0.3578 3% } $\ \rm bit$ | ||
| − | { | + | {Which value results for the equivocation $H(X|Y)$? |
|type="{}"} | |type="{}"} | ||
$H(X|Y) \ = \ $ { 0.3642 3% } $\ \rm bit$ | $H(X|Y) \ = \ $ { 0.3642 3% } $\ \rm bit$ | ||
| − | { | + | {Which statement is true for the sink entropy $H(Y)$ ? |
|type="[]"} | |type="[]"} | ||
| − | - $H(Y)$ | + | - $H(Y)$ is never greater than $H(X)$. |
| − | + $H(Y)$ | + | + $H(Y)$ is never smaller than $H(X)$. |
| − | { | + | {Which statement is true for the irrelevance $H(Y|X)$ ? |
|type="[]"} | |type="[]"} | ||
| − | - $H(Y|X)$ | + | - $H(Y|X)$ is never larger than the equivocation $H(X|Y)$. |
| − | + $H(Y|X)$ | + | + $H(Y|X)$ is never smaller than the equivocation $H(X|Y)$. |
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' The following applies in general or with the numerical values $p_0 = 0.2$ and $\varepsilon = 0.1$ for the quantities sought: |
:$$P_{XY}(0, 0) = p_0 \cdot (1 - \varepsilon) | :$$P_{XY}(0, 0) = p_0 \cdot (1 - \varepsilon) | ||
\hspace{0.15cm} \underline {=0.18} \hspace{0.05cm}, \hspace{0.5cm} | \hspace{0.15cm} \underline {=0.18} \hspace{0.05cm}, \hspace{0.5cm} | ||
| Line 96: | Line 96: | ||
| − | '''(2)''' | + | '''(2)''' In general: |
:$$P_Y(Y) = \big [ {\rm Pr}( Y = 0)\hspace{0.05cm}, {\rm Pr}( Y = 1) \big ] = \big ( p_0\hspace{0.05cm}, p_1 \big ) \cdot \begin{pmatrix} 1 - \varepsilon & \varepsilon\\ \varepsilon & 1 - \varepsilon \end{pmatrix}.$$ | :$$P_Y(Y) = \big [ {\rm Pr}( Y = 0)\hspace{0.05cm}, {\rm Pr}( Y = 1) \big ] = \big ( p_0\hspace{0.05cm}, p_1 \big ) \cdot \begin{pmatrix} 1 - \varepsilon & \varepsilon\\ \varepsilon & 1 - \varepsilon \end{pmatrix}.$$ | ||
| − | + | This gives the following numerical values: | |
:$$ {\rm Pr}( Y = 0)= p_0 \cdot (1 - \varepsilon) + p_1 \cdot \varepsilon = 0.2 \cdot 0.9 + 0.8 \cdot 0.1 \hspace{0.15cm} \underline {=0.26} \hspace{0.05cm},$$ | :$$ {\rm Pr}( Y = 0)= p_0 \cdot (1 - \varepsilon) + p_1 \cdot \varepsilon = 0.2 \cdot 0.9 + 0.8 \cdot 0.1 \hspace{0.15cm} \underline {=0.26} \hspace{0.05cm},$$ | ||
:$${\rm Pr}( Y = 1)= p_0 \cdot \varepsilon + p_1 \cdot (1 - \varepsilon) = 0.2 \cdot 0.1 + 0.8 \cdot 0.9 \hspace{0.15cm} \underline {=0.74} \hspace{0.05cm}.$$ | :$${\rm Pr}( Y = 1)= p_0 \cdot \varepsilon + p_1 \cdot (1 - \varepsilon) = 0.2 \cdot 0.1 + 0.8 \cdot 0.9 \hspace{0.15cm} \underline {=0.74} \hspace{0.05cm}.$$ | ||
| Line 104: | Line 104: | ||
| − | '''(3)''' | + | '''(3)''' For the mutual information, according to the definition with $p_0 = 0.2$, $p_1 = 0.8$ and $\varepsilon = 0.1$: |
:$$I(X;Y) = {\rm E} \hspace{-0.08cm}\left [ \hspace{0.02cm}{\rm log}_2 \hspace{0.08cm} \frac{P_{XY}(X, Y)} {P_{X}(X) \hspace{-0.05cm}\cdot \hspace{-0.05cm} P_{Y}(Y) }\right ] \hspace{0.3cm} \Rightarrow$$ | :$$I(X;Y) = {\rm E} \hspace{-0.08cm}\left [ \hspace{0.02cm}{\rm log}_2 \hspace{0.08cm} \frac{P_{XY}(X, Y)} {P_{X}(X) \hspace{-0.05cm}\cdot \hspace{-0.05cm} P_{Y}(Y) }\right ] \hspace{0.3cm} \Rightarrow$$ | ||
:$$I(X;Y) = 0.18 \cdot {\rm log}_2 \hspace{0.1cm} \frac{0.18}{0.2 \hspace{-0.05cm}\cdot \hspace{-0.05cm} 0.26} + 0.02 \cdot {\rm log}_2 \hspace{0.08cm} \frac{0.02}{0.2 \hspace{-0.05cm}\cdot \hspace{-0.05cm} 0.74} | :$$I(X;Y) = 0.18 \cdot {\rm log}_2 \hspace{0.1cm} \frac{0.18}{0.2 \hspace{-0.05cm}\cdot \hspace{-0.05cm} 0.26} + 0.02 \cdot {\rm log}_2 \hspace{0.08cm} \frac{0.02}{0.2 \hspace{-0.05cm}\cdot \hspace{-0.05cm} 0.74} | ||
| Line 111: | Line 111: | ||
| − | '''(4)''' | + | '''(4)''' With the source entropy $H(X)$ given, we obtain for the equivocation: |
:$$H(X \hspace{-0.1cm}\mid \hspace{-0.1cm} Y) = H(X) - I(X;Y) = 0.7219 - 0.3578 \hspace{0.15cm} \underline {=0.3642\,{\rm bit}} \hspace{0.05cm}.$$ | :$$H(X \hspace{-0.1cm}\mid \hspace{-0.1cm} Y) = H(X) - I(X;Y) = 0.7219 - 0.3578 \hspace{0.15cm} \underline {=0.3642\,{\rm bit}} \hspace{0.05cm}.$$ | ||
| − | * | + | *However, one could also apply the general definition with the inference probabilities $P_{X|Y}(⋅)$ : |
:$$H(X \hspace{-0.1cm}\mid \hspace{-0.1cm} Y) = {\rm E} \hspace{0.02cm} \left [ \hspace{0.05cm} {\rm log}_2 \hspace{0.1cm} \frac{1}{P_{\hspace{0.03cm}X \mid \hspace{0.03cm} Y} (X \hspace{-0.05cm}\mid \hspace{-0.05cm} Y)} \hspace{0.05cm}\right ] = {\rm E} \hspace{0.02cm} \left [ \hspace{0.05cm} {\rm log}_2 \hspace{0.1cm} \frac{P_Y(Y)}{P_{XY} (X, Y)} \hspace{0.05cm} \right ] \hspace{0.05cm}$$ | :$$H(X \hspace{-0.1cm}\mid \hspace{-0.1cm} Y) = {\rm E} \hspace{0.02cm} \left [ \hspace{0.05cm} {\rm log}_2 \hspace{0.1cm} \frac{1}{P_{\hspace{0.03cm}X \mid \hspace{0.03cm} Y} (X \hspace{-0.05cm}\mid \hspace{-0.05cm} Y)} \hspace{0.05cm}\right ] = {\rm E} \hspace{0.02cm} \left [ \hspace{0.05cm} {\rm log}_2 \hspace{0.1cm} \frac{P_Y(Y)}{P_{XY} (X, Y)} \hspace{0.05cm} \right ] \hspace{0.05cm}$$ | ||
| − | * | + | *In the example, the same result $H(X|Y) = 0.3642 \ \rm bit$ is also obtained according to this calculation rule: |
:$$H(X \hspace{-0.1cm}\mid \hspace{-0.1cm} Y) = 0.18 \cdot {\rm log}_2 \hspace{0.1cm} \frac{0.26}{0.18} + 0.02 \cdot {\rm log}_2 \hspace{0.1cm} \frac{0.74}{0.02} + 0.08 \cdot {\rm log}_2 \hspace{0.1cm} \frac{0.26}{0.08} + 0.72 \cdot {\rm log}_2 \hspace{0.1cm} \frac{0.74}{0.72} \hspace{0.05cm}.$$ | :$$H(X \hspace{-0.1cm}\mid \hspace{-0.1cm} Y) = 0.18 \cdot {\rm log}_2 \hspace{0.1cm} \frac{0.26}{0.18} + 0.02 \cdot {\rm log}_2 \hspace{0.1cm} \frac{0.74}{0.02} + 0.08 \cdot {\rm log}_2 \hspace{0.1cm} \frac{0.26}{0.08} + 0.72 \cdot {\rm log}_2 \hspace{0.1cm} \frac{0.74}{0.72} \hspace{0.05cm}.$$ | ||
| − | '''(5)''' | + | '''(5)''' Correct is the <u>proposed solution 2:</u> |
| − | * | + | *In the case of disturbed transmission $(ε > 0)$ the uncertainty regarding the sink is always greater than the uncertainty regarding the source. One obtains here as a numerical value: |
:$$H(Y) = H_{\rm bin}(0.26)={ 0.8268\,{\rm bit}} \hspace{0.05cm}.$$ | :$$H(Y) = H_{\rm bin}(0.26)={ 0.8268\,{\rm bit}} \hspace{0.05cm}.$$ | ||
| − | * | + | *With error-free transmission $(ε = 0)$ , on the other hand, $P_Y(⋅) = P_X(⋅)$ and $H(Y) = H(X)$ would apply. |
| − | '''(6)''' | + | '''(6)''' Here, too, the <u>second proposed solution</u> is correct: |
| − | * | + | *Because of $I(X;Y) = H(X) - H(X \hspace{-0.1cm}\mid \hspace{-0.1cm} Y) = H(Y) - H(Y \hspace{-0.1cm}\mid \hspace{-0.1cm} X)$ , $H(Y|X)$ by the same amount that $H(X|Y)$, um den $H(Y)$ is greater than $H(X)$: |
:$$H(Y \hspace{-0.1cm}\mid \hspace{-0.1cm} X) = H(Y) -I(X;Y) = 0.8268 - 0.3578 ={ 0.4690\,{\rm bit}} \hspace{0.05cm}$$ | :$$H(Y \hspace{-0.1cm}\mid \hspace{-0.1cm} X) = H(Y) -I(X;Y) = 0.8268 - 0.3578 ={ 0.4690\,{\rm bit}} \hspace{0.05cm}$$ | ||
| − | * | + | *Direct calculation gives the same result $H(Y|X) = 0.4690\ \rm bit$: |
:$$H(Y \hspace{-0.1cm}\mid \hspace{-0.1cm} X) = {\rm E} \hspace{0.02cm} \left [ \hspace{0.02cm} {\rm log}_2 \hspace{0.1cm} \frac{1}{P_{\hspace{0.03cm}Y \mid \hspace{0.03cm} X} (Y \hspace{-0.05cm}\mid \hspace{-0.05cm} X)} \right ] = 0.18 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.9} + 0.02 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.1} + 0.08 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.1} + 0.72 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.9} \hspace{0.05cm}.$$ | :$$H(Y \hspace{-0.1cm}\mid \hspace{-0.1cm} X) = {\rm E} \hspace{0.02cm} \left [ \hspace{0.02cm} {\rm log}_2 \hspace{0.1cm} \frac{1}{P_{\hspace{0.03cm}Y \mid \hspace{0.03cm} X} (Y \hspace{-0.05cm}\mid \hspace{-0.05cm} X)} \right ] = 0.18 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.9} + 0.02 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.1} + 0.08 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.1} + 0.72 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.9} \hspace{0.05cm}.$$ | ||
Revision as of 11:30, 14 September 2021
We consider the Binary Symmetric Channel $\rm (BSC)$. The parameter values are valid for the whole exercise:
- Probability of falsification: $\varepsilon = 0.1$,
- Probability for $0$: $p_0 = 0.2$,
- Probability for $1$: $p_1 = 0.8$.
Thus the probability function of the source is: $P_X(X)= (0.2 , \ 0.8)$ and for the source entropy applies:
- $$H(X) = p_0 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{p_0} + p_1\cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{p_1} = H_{\rm bin}(0.2)={ 0.7219\,{\rm bit}} \hspace{0.05cm}.$$
The task is to determine:
- the probability function of the sink:
- $$P_Y(Y) = (\hspace{0.05cm}P_Y(0)\hspace{0.05cm}, \ \hspace{0.05cm} P_Y(1)\hspace{0.05cm}) \hspace{0.05cm},$$
- the joint probability function:
- $$P_{XY}(X, Y) = \begin{pmatrix} p_{00} & p_{01}\\ p_{10} & p_{11} \end{pmatrix} \hspace{0.05cm},$$
- the mutual information:
- $$I(X;Y) = {\rm E} \hspace{-0.08cm}\left [ \hspace{0.02cm}{\rm log}_2 \hspace{0.1cm} \frac{P_{XY}(X, Y)} {P_{X}(X) \cdot P_{Y}(Y) }\right ] \hspace{0.05cm},$$
- the equivocation:
- $$H(X \hspace{-0.1cm}\mid \hspace{-0.1cm} Y) = {\rm E} \hspace{0.02cm} \big [ \hspace{0.02cm} {\rm log}_2 \hspace{0.1cm} \frac{1}{P_{\hspace{0.03cm}X \mid \hspace{0.03cm} Y} (X \hspace{-0.05cm}\mid \hspace{-0.05cm} Y)} \big ] \hspace{0.05cm},$$
- the irrelevance:
- $$H(Y \hspace{-0.1cm}\mid \hspace{-0.1cm} X) = {\rm E} \hspace{0.02cm} \big [ \hspace{0.02cm} {\rm log}_2 \hspace{0.1cm} \frac{1}{P_{\hspace{0.03cm}Y \mid \hspace{0.03cm} X} (Y \hspace{-0.05cm}\mid \hspace{-0.05cm} X)} \big ] \hspace{0.05cm}.$$
Hints:
- The task belongs to the chapter Application to Digital Signal Transmission.
- Bezug genommen wird insbesondere auf die Seite Mutual information calculation for the binary channel.
- In task 3.10Z the channel capacity $C_{\rm BSC }$ of the BSC model is calculated.
- This results as the maximum mutual information $I(X;\ Y)$ by maximisation with respect to the probabilities $p_0$ or $p_1 = 1 - p_0$.
Questions
Solution
(1) The following applies in general or with the numerical values $p_0 = 0.2$ and $\varepsilon = 0.1$ for the quantities sought:
- $$P_{XY}(0, 0) = p_0 \cdot (1 - \varepsilon) \hspace{0.15cm} \underline {=0.18} \hspace{0.05cm}, \hspace{0.5cm} P_{XY}(0, 1) = p_0 \cdot \varepsilon \hspace{0.15cm} \underline {=0.02} \hspace{0.05cm},$$
- $$P_{XY}(1, 0) = p_1 \cdot \varepsilon \hspace{0.15cm} \underline {=0.08} \hspace{0.05cm}, \hspace{1.55cm} P_{XY}(1, 1) = p_1 \cdot (1 - \varepsilon) \hspace{0.15cm} \underline {=0.72} \hspace{0.05cm}.$$
(2) In general:
- $$P_Y(Y) = \big [ {\rm Pr}( Y = 0)\hspace{0.05cm}, {\rm Pr}( Y = 1) \big ] = \big ( p_0\hspace{0.05cm}, p_1 \big ) \cdot \begin{pmatrix} 1 - \varepsilon & \varepsilon\\ \varepsilon & 1 - \varepsilon \end{pmatrix}.$$
This gives the following numerical values:
- $$ {\rm Pr}( Y = 0)= p_0 \cdot (1 - \varepsilon) + p_1 \cdot \varepsilon = 0.2 \cdot 0.9 + 0.8 \cdot 0.1 \hspace{0.15cm} \underline {=0.26} \hspace{0.05cm},$$
- $${\rm Pr}( Y = 1)= p_0 \cdot \varepsilon + p_1 \cdot (1 - \varepsilon) = 0.2 \cdot 0.1 + 0.8 \cdot 0.9 \hspace{0.15cm} \underline {=0.74} \hspace{0.05cm}.$$
(3) For the mutual information, according to the definition with $p_0 = 0.2$, $p_1 = 0.8$ and $\varepsilon = 0.1$:
- $$I(X;Y) = {\rm E} \hspace{-0.08cm}\left [ \hspace{0.02cm}{\rm log}_2 \hspace{0.08cm} \frac{P_{XY}(X, Y)} {P_{X}(X) \hspace{-0.05cm}\cdot \hspace{-0.05cm} P_{Y}(Y) }\right ] \hspace{0.3cm} \Rightarrow$$
- $$I(X;Y) = 0.18 \cdot {\rm log}_2 \hspace{0.1cm} \frac{0.18}{0.2 \hspace{-0.05cm}\cdot \hspace{-0.05cm} 0.26} + 0.02 \cdot {\rm log}_2 \hspace{0.08cm} \frac{0.02}{0.2 \hspace{-0.05cm}\cdot \hspace{-0.05cm} 0.74} + 0.08 \cdot {\rm log}_2 \hspace{0.08cm} \frac{0.08}{0.8 \hspace{-0.05cm}\cdot \hspace{-0.05cm} 0.26} + 0.72 \cdot {\rm log}_2 \hspace{0.08cm} \frac{0.72}{0.8 \hspace{-0.05cm}\cdot \hspace{-0.05cm} 0.74} \hspace{0.15cm} \underline {=0.3578\,{\rm bit}} \hspace{0.05cm}.$$
(4) With the source entropy $H(X)$ given, we obtain for the equivocation:
- $$H(X \hspace{-0.1cm}\mid \hspace{-0.1cm} Y) = H(X) - I(X;Y) = 0.7219 - 0.3578 \hspace{0.15cm} \underline {=0.3642\,{\rm bit}} \hspace{0.05cm}.$$
- However, one could also apply the general definition with the inference probabilities $P_{X|Y}(⋅)$ :
- $$H(X \hspace{-0.1cm}\mid \hspace{-0.1cm} Y) = {\rm E} \hspace{0.02cm} \left [ \hspace{0.05cm} {\rm log}_2 \hspace{0.1cm} \frac{1}{P_{\hspace{0.03cm}X \mid \hspace{0.03cm} Y} (X \hspace{-0.05cm}\mid \hspace{-0.05cm} Y)} \hspace{0.05cm}\right ] = {\rm E} \hspace{0.02cm} \left [ \hspace{0.05cm} {\rm log}_2 \hspace{0.1cm} \frac{P_Y(Y)}{P_{XY} (X, Y)} \hspace{0.05cm} \right ] \hspace{0.05cm}$$
- In the example, the same result $H(X|Y) = 0.3642 \ \rm bit$ is also obtained according to this calculation rule:
- $$H(X \hspace{-0.1cm}\mid \hspace{-0.1cm} Y) = 0.18 \cdot {\rm log}_2 \hspace{0.1cm} \frac{0.26}{0.18} + 0.02 \cdot {\rm log}_2 \hspace{0.1cm} \frac{0.74}{0.02} + 0.08 \cdot {\rm log}_2 \hspace{0.1cm} \frac{0.26}{0.08} + 0.72 \cdot {\rm log}_2 \hspace{0.1cm} \frac{0.74}{0.72} \hspace{0.05cm}.$$
(5) Correct is the proposed solution 2:
- In the case of disturbed transmission $(ε > 0)$ the uncertainty regarding the sink is always greater than the uncertainty regarding the source. One obtains here as a numerical value:
- $$H(Y) = H_{\rm bin}(0.26)={ 0.8268\,{\rm bit}} \hspace{0.05cm}.$$
- With error-free transmission $(ε = 0)$ , on the other hand, $P_Y(⋅) = P_X(⋅)$ and $H(Y) = H(X)$ would apply.
(6) Here, too, the second proposed solution is correct:
- Because of $I(X;Y) = H(X) - H(X \hspace{-0.1cm}\mid \hspace{-0.1cm} Y) = H(Y) - H(Y \hspace{-0.1cm}\mid \hspace{-0.1cm} X)$ , $H(Y|X)$ by the same amount that $H(X|Y)$, um den $H(Y)$ is greater than $H(X)$:
- $$H(Y \hspace{-0.1cm}\mid \hspace{-0.1cm} X) = H(Y) -I(X;Y) = 0.8268 - 0.3578 ={ 0.4690\,{\rm bit}} \hspace{0.05cm}$$
- Direct calculation gives the same result $H(Y|X) = 0.4690\ \rm bit$:
- $$H(Y \hspace{-0.1cm}\mid \hspace{-0.1cm} X) = {\rm E} \hspace{0.02cm} \left [ \hspace{0.02cm} {\rm log}_2 \hspace{0.1cm} \frac{1}{P_{\hspace{0.03cm}Y \mid \hspace{0.03cm} X} (Y \hspace{-0.05cm}\mid \hspace{-0.05cm} X)} \right ] = 0.18 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.9} + 0.02 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.1} + 0.08 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.1} + 0.72 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.9} \hspace{0.05cm}.$$