Difference between revisions of "Aufgaben:Exercise 3.11: Erasure Channel"
| (3 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Information_Theory/Application_to_Digital_Signal_Transmission |
}} | }} | ||
| Line 29: | Line 29: | ||
*The exercise belongs to the chapter [[Information_Theory/Anwendung_auf_die_Digitalsignalübertragung|Application to Digital Signal Transmission]]. | *The exercise belongs to the chapter [[Information_Theory/Anwendung_auf_die_Digitalsignalübertragung|Application to Digital Signal Transmission]]. | ||
*Reference is made in particular to the page [[Information_Theory/Anwendung_auf_die_Digitalsignalübertragung#Information-theoretical_model_of_digital_signal_transmission|Information-theoretical model of digital signal transmission]]. | *Reference is made in particular to the page [[Information_Theory/Anwendung_auf_die_Digitalsignalübertragung#Information-theoretical_model_of_digital_signal_transmission|Information-theoretical model of digital signal transmission]]. | ||
| − | *In the above diagram, | + | *In the above diagram, "erasures" $($with probability $λ)$ are drawn in blue. |
* "Correct transmission paths" $($i.e., from $X = μ$ to $Y = μ)$ are shown in red ($1 ≤ μ ≤ M$). | * "Correct transmission paths" $($i.e., from $X = μ$ to $Y = μ)$ are shown in red ($1 ≤ μ ≤ M$). | ||
| Line 38: | Line 38: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { What $P_X(X)$ should be generally applied for channel capacity calculation? | + | { What $P_X(X)$ should be generally applied for the channel capacity calculation? |
|type="[]"} | |type="[]"} | ||
- $P_X(X) = (0.5, \ 0.5),$ | - $P_X(X) = (0.5, \ 0.5),$ | ||
| Line 83: | Line 83: | ||
| − | '''(2)''' Correct is the <u>proposed solution 3</u>, i.e. exactly $2M$ connections. | + | '''(2)''' Correct is the <u>proposed solution 3</u>, i.e. exactly $2M$ connections. Because: |
*From each source symbol $X = μ$ one gets to the sink symbol $Y = μ$ as well as to the erasure $Y = \text{E}$. | *From each source symbol $X = μ$ one gets to the sink symbol $Y = μ$ as well as to the erasure $Y = \text{E}$. | ||
| Line 125: | Line 125: | ||
| − | '''(6)''' The | + | '''(6)''' The "Binary Erasure Channel" $\rm (BEC)$ is a special case of the general model considered here with $M = 2$: |
:$$C_{\rm BEC} = 1-\lambda \hspace{0.05cm}.$$ | :$$C_{\rm BEC} = 1-\lambda \hspace{0.05cm}.$$ | ||
*Thus, the correct <u>solution proposal 1</u>. | *Thus, the correct <u>solution proposal 1</u>. | ||
| − | *The second proposed solution, on the other hand, applies to the | + | *The second proposed solution, on the other hand, applies to the "Binary Symmetric Channel" $\rm (BSC)$ with distortion probability $λ$. |
{{ML-Fuß}} | {{ML-Fuß}} | ||
| Line 134: | Line 134: | ||
| − | [[Category:Information Theory: Exercises|^3.3 | + | [[Category:Information Theory: Exercises|^3.3 Application to Digital Signal Transmission^]] |
Latest revision as of 13:56, 24 September 2021
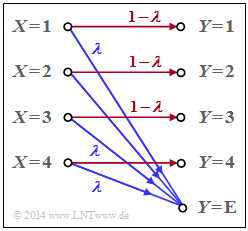
An erasure channel is considered with
- the $M$ inputs $x ∈ X = \{1,\ 2, \ \text{...} \ ,\ M\}$, and
- the $M + 1$ outputs $y ∈ Y = \{1,\ 2,\ \ \text{...} \ ,\ M,\ \text{E}\}.$
The graph shows the model for the special case $M = 4$. The sink symbol $y = \text{E}$ takes into account an erasure for the case that the receiver cannot make a sufficiently certain decision.
The transition probabilities are given for $1 ≤ μ ≤ M$ as follows:
- $${\rm Pr}(Y \hspace{-0.05cm} = \mu\hspace{-0.05cm}\mid \hspace{-0.05cm} X \hspace{-0.05cm}= \mu) = 1-\lambda \hspace{0.05cm},$$
- $${\rm Pr}(Y \hspace{-0.05cm} = {\rm E}\hspace{-0.05cm}\mid \hspace{-0.05cm} X \hspace{-0.05cm}= \mu) = \lambda \hspace{0.05cm}.$$
We are looking for:
- the capacity $C_{M\rm –EC}$ of this M–ary Erasure Channel,
- the capacity $C_{\rm BEC}$ of the Binary Erasure Channels as a special case of the above model.
Hints:
- The exercise belongs to the chapter Application to Digital Signal Transmission.
- Reference is made in particular to the page Information-theoretical model of digital signal transmission.
- In the above diagram, "erasures" $($with probability $λ)$ are drawn in blue.
- "Correct transmission paths" $($i.e., from $X = μ$ to $Y = μ)$ are shown in red ($1 ≤ μ ≤ M$).
Questions
Solution
- Due to the symmetry of the transition probabilities $P_{Y|X}(Y|X)$ it is obvious that a uniform distribution will lead to the maximum mutual information $I(X; Y)$ and therefore to the channel capacity $C$ :
- $$ P_X(X) = P_X\big ( \hspace{0.03cm}X\hspace{-0.03cm}=1\hspace{0.03cm}, \hspace{0.08cm} X\hspace{-0.03cm}=2\hspace{0.03cm},\hspace{0.08cm}\text{...}\hspace{0.08cm}, X\hspace{-0.03cm}=M\hspace{0.03cm}\big ) = \big [\hspace{0.03cm}1/M\hspace{0.03cm}, \hspace{0.08cm} 1/M\hspace{0.03cm},\hspace{0.03cm}\text{...}\hspace{0.08cm},\hspace{0.08cm} 1/M\hspace{0.03cm}\big ]\hspace{0.05cm}.$$
- In the special case $M = 2$ also $P_X(X) = (0.5, \ 0.5)$ would be correct.
(2) Correct is the proposed solution 3, i.e. exactly $2M$ connections. Because:
- From each source symbol $X = μ$ one gets to the sink symbol $Y = μ$ as well as to the erasure $Y = \text{E}$.
(3) All probabilities ${\rm Pr}(Y = 1), \hspace{0.05cm} \text{...}\hspace{0.05cm} , \hspace{0.08cm}{\rm Pr}(Y = M)$ are equal. Thus, for $μ = 1, \hspace{0.05cm} \text{...} \hspace{0.05cm} , \hspace{0.08cm} M$ we obtain:
- $${\rm Pr}(Y \hspace{-0.05cm} = \mu) = ( 1-\lambda)/M \hspace{0.05cm}.$$
- Moreover, from each source symbol $X = 1, \hspace{0.05cm} \text{...}\hspace{0.05cm} , X = M$ one also gets to the erasure $Y = \text{E}$:
- $${\rm Pr}(Y \hspace{-0.05cm} = {\rm E}) = \lambda \hspace{0.05cm}.$$
- Inspection reveals that the sum of all $M + 1$ sink symbol probabilities actually adds up t $1$ .
- It follows for the sink entropy:
- $$H(Y) = M \cdot \frac{ 1-\lambda }{M} \cdot {\rm log}_2 \hspace{0.1cm} \frac{M}{1 - \lambda} \hspace{0.15cm}+\hspace{0.15cm} \lambda \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{\lambda} \hspace{0.05cm}.$$
- Summarized with the binary entropy function, this gives:
- $$H(Y) = (1-\lambda) \cdot {\rm log}_2 \hspace{0.1cm} M \hspace{0.15cm}+\hspace{0.15cm} H_{\rm bin} (\lambda ) \hspace{0.05cm}$$
- and with $M = 4$ as well as $ λ = 0.2$:
- $$H(Y) = 1.6 \,{\rm bit} + H_{\rm bin} (0.2 ) \hspace{0.15cm} \underline {=2.322\,{\rm bit}} \hspace{0.05cm}.$$
(4) The $2M$ joint probabilities
- $${\rm Pr} \big[(X = μ) ∩ (Y = κ)\big] ≠ 0$$
- and the conditional probabilities
- $$pκ|μ = {\rm Pr}(Y = κ|X = μ)$$
- show the following properties:
- The combination $p_{μκ} = (1 – λ)/M$ and $p_{κ|μ} = 1 – λ$ occurs $M$ times.
- The combination $p_{μκ} = λ/M$ and $p_{κ|μ} = λ$ also occurs $M$ times.
It follows that:
- $$ H(Y \hspace{-0.15cm}\mid \hspace{-0.15cm} X) \hspace{-0.01cm} =\hspace{-0.01cm} M \cdot \frac{ 1-\lambda }{M} \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{1 - \lambda} \hspace{0.15cm}+\hspace{0.15cm}M \cdot \frac{ \lambda }{M} \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{ \lambda} = ( 1-\lambda) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{1 - \lambda} \hspace{0.15cm}+\hspace{0.15cm} \lambda \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{ \lambda} = H_{\rm bin} (\lambda)\hspace{0.05cm}.$$
- The result is independent of $M$. With $λ = 0.2$ we obtain:
- $$H(Y \hspace{-0.1cm}\mid \hspace{-0.1cm} X) = H_{\rm bin} (0.2 ) \hspace{0.15cm} \underline {=0.722\,{\rm bit}} \hspace{0.05cm}.$$
(5) The channel capacity $C$ is equal to the maximum mutual information $I(X; Y)$, where the maximization with respect to $P_X(X)$ has already been considered by the symmetric approach:
- $$ C = \max_{P_X(X)} \hspace{0.15cm} I(X;Y) = H(Y) - H(Y \hspace{-0.1cm}\mid \hspace{-0.1cm} X) = ( 1-\lambda) \cdot {\rm log}_2 \hspace{0.1cm} M + H_{\rm bin} (\lambda) - H_{\rm bin} (\lambda) = ( 1-\lambda) \cdot {\rm log}_2 \hspace{0.1cm} M \hspace{0.05cm}$$
- $$\Rightarrow \hspace{0.3cm} M = 4\text{:} \hspace{0.3cm} \underline {C=1.6\,\,{\rm bit}} \hspace{0.05cm}, \hspace{0.8cm} M = 2\text{:} \hspace{0.3cm} \underline {C=0.8\,\,{\rm bit}} \hspace{0.05cm}.$$
(6) The "Binary Erasure Channel" $\rm (BEC)$ is a special case of the general model considered here with $M = 2$:
- $$C_{\rm BEC} = 1-\lambda \hspace{0.05cm}.$$
- Thus, the correct solution proposal 1.
- The second proposed solution, on the other hand, applies to the "Binary Symmetric Channel" $\rm (BSC)$ with distortion probability $λ$.