Difference between revisions of "Aufgaben:Exercise 3.2: CDF for Exercise 3.1"
From LNTwww
m (Textersetzung - „*Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.“ durch „ “) |
|||
| (16 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Theory_of_Stochastic_Signals/Cumulative_Distribution_Function |
}} | }} | ||
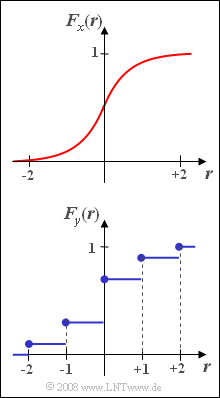
| − | [[File:P_ID114__Sto_A_3_2.png|right| | + | [[File:P_ID114__Sto_A_3_2.png|right|frame|Given cumulative distribution function $\rm (CDF)$]] |
| − | + | The same conditions apply as for [[Aufgaben:Exercise_3.1:_cos²-PDF_and_PDF_with_Dirac_Functions|Exercise 3.1]]. | |
| − | * | + | *The PDF of the continuous valued random variable is identically zero in the ranges $|x| > 2$. |
| + | *In the range $-2 \le x \le +2$ holds: | ||
:$$f_x(x)={1}/{2}\cdot \cos^2({\pi}/{4}\cdot x).$$ | :$$f_x(x)={1}/{2}\cdot \cos^2({\pi}/{4}\cdot x).$$ | ||
| − | * | + | *The discrete valued random variable $y$ is limited too to the range $\pm 2$ Here, the following probabilities apply: |
:$${\rm \Pr}(y=0)=0.4,$$ | :$${\rm \Pr}(y=0)=0.4,$$ | ||
:$${\rm \Pr}(y=+1)={\rm \Pr}(y=-1)=0.2,$$ | :$${\rm \Pr}(y=+1)={\rm \Pr}(y=-1)=0.2,$$ | ||
| Line 14: | Line 15: | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | === | + | |
| + | |||
| + | Hints: | ||
| + | *The exercise belongs to the chapter [[Theory_of_Stochastic_Signals/Cumulative_Distribution_Function|Cumulative Distribution Function]]. | ||
| + | *The topic of this chapter is illustrated with examples in the (German language) learning video <br> [[Zusammenhang_zwischen_WDF_und_VTF_(Lernvideo)|"Zusammenhang zwischen WDF und VTF"]] $\Rightarrow$ "Relationship between PDF and CDF". | ||
| + | *Given the following equation: | ||
| + | :$$\int \cos^{\rm 2}( ax)\, {\rm d}x=\frac{x}{2}+\frac{1}{4 a}\cdot \sin(2 ax).$$ | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Which of the following statements are true for the cumulative distribution function $F_x(r)$ of the continuous valued random variable $x$ ? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + The CDF is equal for all values $r \le -2$ ⇒ $F_x(r) \equiv 0$. |
| − | + | + | + The CDF is equal for all values $r \ge +2$ ⇒ $F_x(r) \equiv 1$. |
| − | + | + | + The curve of $F_x(r)$ is monotonically increasing. |
| − | { | + | {Which of the following statements are true for the cumulative distribution function $F_y(r)$ of the discrete valued random variable $y$ ? |
|type="[]"} | |type="[]"} | ||
| − | - | + | - The CDF is equal for all values $r \le -2$ ⇒ $F_y(r) \equiv 0$. |
| − | + | + | + The CDF is equal for all values $r \ge +2$ ⇒ $F_y(r) \equiv 1$. |
| − | + | + | + The curve of $F_y(r)$ is monotonically increasing. |
| − | { | + | {Calculate the CDF $F_x(r)$. Restrict yourself to the range $0 \le r \le +2$. What value results for $r = +1$? |
|type="{}"} | |type="{}"} | ||
| − | $F_x(r=+1) \ = $ { 0.909 3% } | + | $F_x(r=+1) \ = \ $ { 0.909 3% } |
| − | { | + | {What is the relationship between $F_x(r)$ and $F_x(-r)$? Enter the CDF value $F_x(r=-1)$. |
|type="{}"} | |type="{}"} | ||
| − | $F_x(r=-1) \ = $ | + | $F_x(r=-1) \ = \ $ { 0.091 3% } |
| + | |||
| + | |||
| − | { | + | {Calculate the probability that $|\hspace{0.05cm}x\hspace{0.05cm}|$ is smaller than $1$. Compare the result with the result of subtask '''(7)''' of Exercise 3.1. |
|type="{}"} | |type="{}"} | ||
| − | ${\rm Pr}(|x| < 1) \ = $ | + | ${\rm Pr}(|\hspace{0.05cm}x\hspace{0.05cm}| < 1) \ = \ $ { 0.818 3% } |
| + | |||
| − | { | + | {What value is obtained for the CDF of the discrete valued random variable $y$ at the location $r = 0$? |
|type="{}"} | |type="{}"} | ||
| − | $F_y(r = 0)\ = $ { 0.7 3% } | + | $F_y(r = 0)\ = \ $ { 0.7 3% } |
| Line 64: | Line 73: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' Since the continuous valued random variable $x$ is limited to the range $|\hspace{0.05cm}x\hspace{0.05cm}< 2|$, <u>all three given statements</u> are correct. |
| + | |||
| + | |||
| + | |||
| + | '''(2)''' Only <u>statements 2 and 3</u> are correct here: | ||
| + | *For a discrete valued random variable, the cumulative distribution function increases only weakly monotonically. | ||
| + | * That means: Except for unit steps, there are only horizontal sections of the CDF. | ||
| + | *Since at the unit step points the right-hand side limit value ⇒ $F_y(-2) = 0.1$, i.e. not equal to zero. | ||
| + | |||
| + | |||
| + | |||
| + | '''(3)''' The CDF $F_x(r)$ is calculated as the integral from $-\infty$ to $r$ over the PDF $f_x(x)$. | ||
| + | |||
| + | *Due to symmetry, herefore can be written in the range $0 \le r \le +2$: | ||
| + | :$$F_{x} (r) =\frac{1}{2} + \int_{0}^{r} f_x(x)\;{\rm d}x = \frac{1}{2} + \int_{0}^{ r} {1}/{2}\cdot \cos^2 ({\pi}/{4}\cdot x)\;{\rm d}x.$$ | ||
| − | '''( | + | *In the same way as for the subtask '''(7)''' of Exercise 3.1, we thus obtain: |
| − | + | :$$F_{x} (r) =\frac{1}{2} + \frac{ r}{ 4} + \frac{1}{2 \pi} \cdot \sin({\pi}/{2}\cdot r),$$ | |
| − | + | :$$F_{x} (r=0) =\rm \frac{1}{2} + \rm \frac{1}{2 \pi} \cdot\rm sin(\rm 0)\hspace{0.15cm}{= 0.500},$$ | |
| + | :$$F_{x} (r=1) =\rm \frac{1}{2} + \frac{\rm 1}{\rm 4} + \rm \frac{1}{2 \pi}\cdot \rm sin({\pi}/{2})\hspace{0.15cm}\underline{=0.909},$$ | ||
| + | :$$F_{x} (r=2) =\rm \frac{1}{2} + \frac{\rm1}{\rm 2} + \rm \frac{1}{2 \pi} \cdot \rm sin(\pi)\hspace{0.15cm}{= 1.000}.$$ | ||
| − | '''( | + | '''(4)''' Because of the point symmetry around $r=0$ resp. $F_{x} (0) = 1/2$ and because of $\sin(-x) = -\sin(x)$ this formula holds in the whole domain, as the following control calculation shows: |
| − | $$F_{x} (r) =\frac{1}{2} | + | :$$F_{x} (r=-2) =\rm \frac{1}{2} - \frac{\rm1}{\rm 2} - \rm \frac{1}{2 \pi} \cdot\rm sin(\pi)=0,$$ |
| + | :$$F_{x} (r=-1) =\rm \frac{1}{2} - \frac{\rm1}{\rm 4} - \rm \frac{1}{2 \pi} \cdot\rm sin({\pi}/{2})\hspace{0.15cm}\underline{= 0.091}.$$ | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | '''( | + | '''(5)''' For the probability that $x$ lies between $-1$ and $+1$: |
| − | $$ | + | :$${\rm Pr}(|\hspace{0.05cm}x\hspace{0.05cm}|< 1)= F_{x}(+1) - F_{ x}(-1)= 0.909-0.091\hspace{0.15cm}\underline{= 0.818}.$$ |
| − | |||
| − | '''( | + | *This result agrees exactly with the result of the subtask '''(7)''' of Exercise 3.1 which was obtained by direct integration üover the WDF. |
| − | |||
| − | |||
| − | |||
| + | '''(6)''' The CDF of the discrete valued random variable $y$ at the location $y =0$ is the sum of the probabilities of $-2$, $-1$ and $0$. So: | ||
| + | :$$F_y(r = 0)\hspace{0.15cm}\underline{= 0.7}.$$ | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category: | + | [[Category:Theory of Stochastic Signals: Exercises|^3.2 Cumulative Distribution Function^]] |
Latest revision as of 16:18, 4 January 2022
The same conditions apply as for Exercise 3.1.
- The PDF of the continuous valued random variable is identically zero in the ranges $|x| > 2$.
- In the range $-2 \le x \le +2$ holds:
- $$f_x(x)={1}/{2}\cdot \cos^2({\pi}/{4}\cdot x).$$
- The discrete valued random variable $y$ is limited too to the range $\pm 2$ Here, the following probabilities apply:
- $${\rm \Pr}(y=0)=0.4,$$
- $${\rm \Pr}(y=+1)={\rm \Pr}(y=-1)=0.2,$$
- $${\rm \Pr}(y=+2)={\rm \Pr}(y=-2)=0.1.$$
Hints:
- The exercise belongs to the chapter Cumulative Distribution Function.
- The topic of this chapter is illustrated with examples in the (German language) learning video
"Zusammenhang zwischen WDF und VTF" $\Rightarrow$ "Relationship between PDF and CDF". - Given the following equation:
- $$\int \cos^{\rm 2}( ax)\, {\rm d}x=\frac{x}{2}+\frac{1}{4 a}\cdot \sin(2 ax).$$
Questions
Solution
(1) Since the continuous valued random variable $x$ is limited to the range $|\hspace{0.05cm}x\hspace{0.05cm}< 2|$, all three given statements are correct.
(2) Only statements 2 and 3 are correct here:
- For a discrete valued random variable, the cumulative distribution function increases only weakly monotonically.
- That means: Except for unit steps, there are only horizontal sections of the CDF.
- Since at the unit step points the right-hand side limit value ⇒ $F_y(-2) = 0.1$, i.e. not equal to zero.
(3) The CDF $F_x(r)$ is calculated as the integral from $-\infty$ to $r$ over the PDF $f_x(x)$.
- Due to symmetry, herefore can be written in the range $0 \le r \le +2$:
- $$F_{x} (r) =\frac{1}{2} + \int_{0}^{r} f_x(x)\;{\rm d}x = \frac{1}{2} + \int_{0}^{ r} {1}/{2}\cdot \cos^2 ({\pi}/{4}\cdot x)\;{\rm d}x.$$
- In the same way as for the subtask (7) of Exercise 3.1, we thus obtain:
- $$F_{x} (r) =\frac{1}{2} + \frac{ r}{ 4} + \frac{1}{2 \pi} \cdot \sin({\pi}/{2}\cdot r),$$
- $$F_{x} (r=0) =\rm \frac{1}{2} + \rm \frac{1}{2 \pi} \cdot\rm sin(\rm 0)\hspace{0.15cm}{= 0.500},$$
- $$F_{x} (r=1) =\rm \frac{1}{2} + \frac{\rm 1}{\rm 4} + \rm \frac{1}{2 \pi}\cdot \rm sin({\pi}/{2})\hspace{0.15cm}\underline{=0.909},$$
- $$F_{x} (r=2) =\rm \frac{1}{2} + \frac{\rm1}{\rm 2} + \rm \frac{1}{2 \pi} \cdot \rm sin(\pi)\hspace{0.15cm}{= 1.000}.$$
(4) Because of the point symmetry around $r=0$ resp. $F_{x} (0) = 1/2$ and because of $\sin(-x) = -\sin(x)$ this formula holds in the whole domain, as the following control calculation shows:
- $$F_{x} (r=-2) =\rm \frac{1}{2} - \frac{\rm1}{\rm 2} - \rm \frac{1}{2 \pi} \cdot\rm sin(\pi)=0,$$
- $$F_{x} (r=-1) =\rm \frac{1}{2} - \frac{\rm1}{\rm 4} - \rm \frac{1}{2 \pi} \cdot\rm sin({\pi}/{2})\hspace{0.15cm}\underline{= 0.091}.$$
(5) For the probability that $x$ lies between $-1$ and $+1$:
- $${\rm Pr}(|\hspace{0.05cm}x\hspace{0.05cm}|< 1)= F_{x}(+1) - F_{ x}(-1)= 0.909-0.091\hspace{0.15cm}\underline{= 0.818}.$$
- This result agrees exactly with the result of the subtask (7) of Exercise 3.1 which was obtained by direct integration üover the WDF.
(6) The CDF of the discrete valued random variable $y$ at the location $y =0$ is the sum of the probabilities of $-2$, $-1$ and $0$. So:
- $$F_y(r = 0)\hspace{0.15cm}\underline{= 0.7}.$$