Aufgaben:Exercise 3.4: GMSK Modulation

• Return to book

Various signals of the GMSK modulation

The modulation method used for GSM is known as Gaussian Minimum Shift Keying (GMSK). This is a type of  Frequency Shift Keying  (FSK) with continuous phase adjustment  $(\rm CP-FSK)$, in which

• the modulation index is smallest possible to still satisfy the orthogonality condition 
      $h = 0.5$   ⇒   Minimum Shift Keying,
• a Gaussian low-pass filter with impulse response  $h_{\rm G}(t)$  is introduced before the FSK modulator,
  to further save bandwidth.

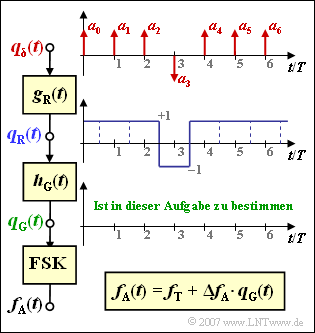
The graphic illustrates the facts:

• The digital message is represented by the amplitude coefficients  $a_{\nu} ∈ ±1$  to which a Dirac pulse is applied. Note that the plotted (red) sequence is assumed for the subtask (3).

• Let the rectangular pulse be dimensionless, symmetric and have the GSM bit duration $T_{\rm B} = T$:

$$g_{\rm R}(t) = \left\{ \begin{array}{c} 1 \\ 0 \\ \end{array} \right.\quad \begin{array}{*{5}c} {\rm{{\rm{for}}}} \\ {\rm{{\rm{for}}}} \\ \end{array}\begin{array}{*{5}c} |\hspace{0.05cm} t \hspace{0.05cm}| < T/2 \hspace{0.05cm}, \\ |\hspace{0.05cm} t \hspace{0.05cm}| > T/2 \hspace{0.05cm}. \\ \end{array}$$

This gives the following for the rectangular wave signal:

$$q_{\rm R} (t) = q_{\rm \delta} (t) \star g_{\rm R}(t) = \sum_{\nu} a_{\nu}\cdot g_{\rm R}(t - \nu \cdot T)\hspace{0.05cm}.$$

• The Gaussian low pass is given by its frequency response or impulse response:

$$H_{\rm G}(f) = {\rm e}^{-\pi\hspace{0.05cm}\cdot \hspace{0.05cm}[f/(2 f_{\rm G})]^2} \hspace{0.2cm}\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\, \hspace{0.2cm} h_{\rm G}(t) = 2 f_{\rm G} \cdot {\rm e}^{-\pi\hspace{0.05cm}\cdot \hspace{0.05cm}(2 f_{\rm G}\cdot t)^2}\hspace{0.05cm},$$

where the system theoretic cutoff frequency  $f_{\rm G}$  is used. However, in the GSM specification, the  $3 \hspace{0.05cm}\rm dB$ cutoff frequency is given as  $f_{\rm 3\hspace{0.05cm} dB} = 0.3/T$ . From this  $f_{\rm G}$  can be calculated directly.

• The signal after the Gaussian low-pass is thus:

$$q_{\rm G} (t) = q_{\rm R} (t) \star h_{\rm G}(t) = \sum_{\nu} a_{\nu}\cdot g(t - \nu \cdot T)\hspace{0.05cm}.$$

Here  $g(t)$  is called the frequency pulse. For this holds:

$$g(t) = q_{\rm R} (t) \star h_{\rm G}(t) \hspace{0.05cm}.$$

• With the low-pass filtered signal  $q_{\rm G}(t)$, the carrier frequency  $f_{\rm T}$  and the frequency deviation  $\delta f_{\rm A}$  can thus be written for the instantaneous frequency at the output of the FSK modulator:

$$f_{\rm A}(t) = f_{\rm T} + \Delta f_{\rm A} \cdot q_{\rm G} (t)\hspace{0.05cm}.$$

For your calculations, use the example values  $f_{\rm T} = 900 \ \rm MHz$  and  $\Delta f_{\rm A} = 68 \ \rm kHz$.

Hints:

Table of the Gaussian error function

• This exercise belongs to the chapter  "Radio Interface".
• Reference is made in particular to the page  "Gaussian Minimum Shift Keying"

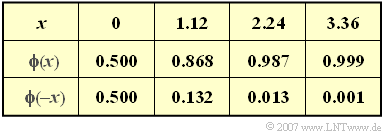
• Use the Gaussian integral to solve this exercise (see adjacent table):

$$\phi(x) =\frac {1}{\sqrt{2 \pi}} \cdot \int^{x} _{-\infty} {\rm e}^{-u^2/2}\,{\rm d}u \hspace{0.05cm}.$$

Questions

1

In what range can the instantaneous frequency  $f_{\rm A}(t)$  vary? What conditions must be met for this to happen?

${\rm Max} \ \big [f_{\rm A}(t) \big ] \ = \ $

2

which system theoretic cutoff frequency of the Gaussian low-pass results from the requirement  $f_{\rm 3\hspace{0.05cm} dB} \cdot T = 0.3$?

$f_{\rm G} \cdot T \ = \ $

3

Calculate the frequency pulse  $g(t)$  using the function  $\Phi (x)$. What is the value of  $g(t = 0)$?

$g(t = 0) \ = \ $

4

What is the value of  $q_{\rm G}(t = 3T)$ if all coefficients except  $a_{3} = -1$  continue  $a_{\nu \neq 3} = +1$  What is the amplitude here  $f_{\rm A}(t = 3T)$?

$q_{\rm G}(t = 3T) \ = \ $

5

Calculate the values  $g(t = ±T)$.

$ g(t = ±T) \ = \ $

6

What is the maximum amplitude of  $q_{\rm G}(t)$  with alternating coefficients? Consider that  $g(t ≥ 2 T) \approx 0$  is.

${\rm Max} \ |q_{\rm G}(t)| \ = \ $

Solution

Solution

(1)  If all amplitude coefficients $a_{\nu}$ are equal to $+1$, $q_{\rm R}(t) = 1$ is a constant.

• The Gaussian low-pass therefore has no effect and $q_{\rm G}(t) = 1$ is obtained.
• The maximum frequency is therefore

$${\rm Max}\hspace{0.05cm}[f_{\rm A}(t)] = f_{\rm T} + \Delta f_{\rm A} \hspace{0.15cm} \underline{= 900.068\,{\rm MHz}} \hspace{0.05cm}.$$

• The minimum of the instantaneous frequency results when all amplitude coefficients are negative:

$${\rm Min}\hspace{0.05cm}[f_{\rm A}(t)] = f_{\rm T} - \Delta f_{\rm A} \hspace{0.15cm} \underline { = 899.932\,{\rm MHz}} \hspace{0.05cm}$$

• In this case, $q_{\rm R}(t) = q_{\rm G}(t) = -1$.

(2)  The frequency at which the logarithmized power transfer function is $3 \ \rm dB$ smaller than $f = 0$ is called the $3\hspace{0.05cm}\rm dB$ cutoff frequency.

• This can also be expressed as follows:

$$\frac {|H(f = f_{\rm 3\hspace{0.05cm}dB})|}{|H(f = 0)|}= \frac{1}{\sqrt{2}} \hspace{0.05cm}.$$

• In particular, for the Gaussian lowpass because of $H(f = 0) = 1$:

$$H(f = f_{\rm 3dB})= {\rm e}^{-\pi\cdot ({f_{\rm 3dB}}/{2 f_{\rm G}})^2} = \frac{1}{\sqrt{2}}\hspace{0.3cm} \Rightarrow \hspace{0.3cm}(\frac{f_{\rm 3dB}}{2 f_{\rm G}})^2 = \frac{{\rm ln}\hspace{0.1cm}\sqrt{2}}{\pi} \hspace{0.3cm}\Rightarrow \hspace{0.3cm}f_{\rm G} = \sqrt{\frac{\pi}{4 \cdot {\rm ln}\hspace{0.1cm}\sqrt{2}}}\cdot f_{\rm 3dB}\hspace{0.05cm}.$$

• The numerical evaluation leads to $f_{\rm G} \approx 1.5 \cdot f_{\rm 3\hspace{0.05cm}dB}$.
• From $f_{\rm 3\hspace{0.05cm}dB} \cdot T = 0.3$ thus follows $f_{\rm G} \cdot T \hspace{0.15cm}\underline{\approx 0.45}$.

(3)  The frequency pulse is obtained by convolution of square wave function $g_{\rm R}(t)$ and impulse response $h_{\rm G}(t)$:

$$g(t) = g_{\rm R} (t) \star h_{\rm G}(t) = 2 f_{\rm G} \cdot \int \limits^{t + T/2} _{t - T/2} {\rm e}^{-\pi\cdot (2 f_{\rm G}\cdot \tau)^2}\,{\rm d}\tau \hspace{0.05cm}.$$

• With the substitution $u^{2 } = 8π \cdot f_{\rm G}^{2} \cdot \tau^{2}$ and the function $\phi (x)$ can also be written for this:

$$g(t) \ = \ \frac {1}{\sqrt{2 \pi}} \cdot \int \limits^{2 \cdot \sqrt{2 \pi} \cdot f_{\rm G} \cdot(t + T/2)} _{2 \cdot \sqrt{2 \pi} \cdot f_{\rm G} \cdot(t - T/2)} {\rm e}^{-u^2/2}\,{\rm d}u = \phi(2 \cdot \sqrt{2 \pi} \cdot f_{\rm G} \cdot(t + T/2))- \phi(2 \cdot \sqrt{2 \pi} \cdot f_{\rm G} \cdot(t - T/2)) \hspace{0.05cm}.$$

• For the time $t = 0$, taking into account $\phi (-x) = 1 - \phi (x)$ and $f_{\rm G} \cdot T = 0.45$:

$$g(t = 0) \ = \ \phi(\sqrt{2 \pi} \cdot f_{\rm G} \cdot T)- \phi(-\sqrt{2 \pi} \cdot f_{\rm G} \cdot T)= 2 \cdot \phi(\sqrt{2 \pi} \cdot f_{\rm G} \cdot T)-1 \approx 2 \cdot \phi(1. 12)-1 \hspace{0.15cm} \underline {= 0.737} \hspace{0.05cm}.$$

(4)  With $a_{3} = +1$, $q_{\rm G}(t = 3 T) = 1$ would result. Thus, due to linearity:

$$q_{\rm G}(t = 3 T ) = 1 - 2 \cdot g(t = 0)= 1 - 2 \cdot 0.737 \hspace{0.15cm} \underline {= -0.474} \hspace{0.05cm}.$$

(5)  Using the result of subtask (3) and $f_{\rm G} \cdot T = 0.45$ we obtain:

$$g(t = T) \ = \ \phi(3 \cdot \sqrt{2 \pi} \cdot f_{\rm G} \cdot T)- \phi(\sqrt{2 \pi} \cdot f_{\rm G} \cdot T) \approx \ \phi(3.36)-\phi(1.12) = 0.999 - 0.868 \hspace{0.15cm} \underline { = 0.131} \hspace{0.05cm}.$$

(6)  In the alternating sequence, for symmetry reasons, the amounts $|q_{\rm G}(\nu \cdot T)|$ are all the same for all multiples of the bit duration $T$.

• All intermediate values at $t \neq \nu - T$ are smaller.
• Considering $g(t ≥ 2T) \approx 0$, every single pulse value $g(0)$ is reduced by the preceding pulse with $g(t = T)$, additionally by the following one with $g(t = -T)$.
• Thus, pulse interference results and one obtains:

$${\rm Max} \hspace{0.08cm}q_{\rm G}(t) = g(0) - 2 \cdot g(T) = 0.737 - 2 \cdot 0.131 \hspace{0.15cm} \underline {= 0.475 }\hspace{0.05cm}.$$