Exercise 3.4Z: Continuous Phase Frequency Shift Keying

Signals for $\text{CP-FSK}$

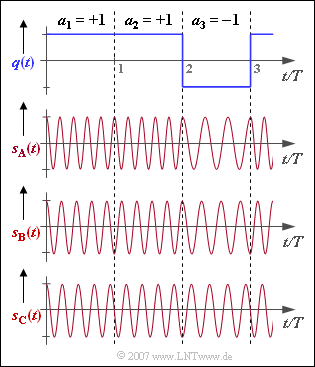
The graph shows three frequency shift keying $\rm (FSK)$ transmitted signals which differ with respect to the frequency deviation $\Delta f_{\rm A}$ distinguish and thus also by their modulation index

$$h = 2 \cdot \Delta f_{\rm A} \cdot T.$$

The digital source signal $q(t)$ underlying the signals $s_{\rm A}(t), s_{\rm B}(t)$ and $s_{\rm C}(t)$ is shown above. All considered signals are normalized to amplitude $1$ and time duration $T$ and based on a cosine carrier with frequency $f_{\rm T}$.

With binary FSK $($"Binary Frequency Shift Keying"$)$ only two different frequencies occur, each of which remains constant over a bit duration:

$f_{1}$ $($if $a_{\nu} = +1)$,

$f_{2}$ $($if $a_{\nu} = -1)$.

If the modulation index is not a multiple of $2$, continuous phase adjustment is required to avoid phase jumps. This is called "Continuous Phase Frequency Shift Keying" $(\text{CP-FSK)}$.

An important special case is represented by binary FSK with modulation index $h = 0.5$ which is also called "Minimum Shift Keying" $(\rm MSK)$. This will be discussed in this exercise.

Hints:

This exercise belongs to the chapter "Radio Interface".

Reference is made in particular to the section "Continuous phase adjustment with FSK.

Questions

Solution

(1) All statements except the third are true:

Generally nonlinear FSK can only be demodulated coherently, while MSK can also use a noncoherent demodulation method.
Compared to QPSK with coherent demodulation, MSK requires $3 \ \rm dB$ more $E_{\rm B}/N_{0}$ (energy per bit related to the noise power density) for the same bit error rate.
The first zero in the power density spectrum occurs later in MSK than in QSPK, but it shows a faster asymptotic decay than in QSPK.
The constant envelope of MSK means that nonlinearities in the transmission line do not play a role. This allows the use of simple and inexpensive power amplifiers with lower power consumption and thus longer operating times of battery-powered devices.

(2) One can see from the graph five and three oscillations per symbol duration, respectively:

$$f_{\rm 1} \cdot T \hspace{0.15cm} \underline {= 5}\hspace{0.05cm},\hspace{0.2cm}f_{\rm 2} \cdot T \hspace{0.15cm} \underline { = 3}\hspace{0.05cm}.$$

(3) For FSK with rectangular pulse shape, only the two instantaneous frequencies $f_{1} = f_{\rm T} + \Delta f_{\rm A}$ and $f_{2} = f_{\rm T} - \Delta f_{\rm A}$ occur.

With the result from (2) we thus obtain:

$$f_{\rm T} \ = \ \frac{f_{\rm 1}+f_{\rm 2}}{2}\hspace{0.3cm}\Rightarrow \hspace{0.3cm}f_{\rm T} \cdot T \hspace{0.15cm} \underline {= 4}\hspace{0.05cm},$$

$$ \Delta f_{\rm A} \ = \ \frac{f_{\rm 1}-f_{\rm 2}}{2}\hspace{0.3cm}\Rightarrow \hspace{0.3cm}\Delta f_{\rm A} \cdot T \hspace{0.15cm} \underline { = 1}\hspace{0.05cm},$$

$$h \ = \ 2 \cdot \Delta f_{\rm A} \cdot T \hspace{0.15cm} \underline {= 2} \hspace{0.05cm}.$$

(4) From the graph one can see the frequencies $f_{1} \cdot T = 4.5$ and $f_{2} \cdot T = 3.5$.

This results in the frequency deviation $\Delta f_{\rm A} \cdot T = 0.5$ and the modulation index $\underline{h = 1}$.

(5) Here the two (normalized) frequencies $f_{1} \cdot T = 4.25$ and $f_{2} \cdot T = 3.75$ occur,

which results in the frequency deviation $\Delta f_{\rm A} \cdot T = 0.25$ and the modulation index $\underline{h = 0.5}$ can be calculated.

(6) Correct are the solutions 2 and 3:

Only at $s_{\rm A}(t)$ was no phase adjustment made.
Here, the signal waveforms in the region of the first and second bit ($a_{1} = a_{2} = +1$) are each cosinusoidal like the carrier signal (with respect to the symbol boundary).
In contrast, in the second symbol of $s_{\rm B}(t)$ a minus-cosine-shaped course (initial phase $\phi_{0} = π$ corresponding to $180^\circ$) can be seen and in the second symbol of $s_{\rm C}(t)$ a minus-sine-shaped course ($\phi_{0} = π /2$ or $90^\circ$).
For $s_{\rm A}(t)$ the initial phase is always $0$, for $s_{\rm B}(t)$ either $0$ or $π$, while for the signal $s_{\rm C}(t)$ with modulation index $h = 0.5$ a total of four initial phases are possible: $0^\circ, \ 90^\circ, \ 180^\circ$ and $270^\circ$.

(7) Correct is the last proposed solution, since for this signal $h = 0.5$ holds.

This is the smallest possible modulation index for which there is orthogonality between $f_{1}$ and $f_{2}$ within the symbol duration $T$.

	FSK is generally a nonlinear modulation method.
	MSK can be implemented as offset QPSK and is therefore linear.
	This results in the same bit error rate as for QPSK.
	A band limitation is less disturbing than with QPSK.
	The MSK envelope is constant even with spectral shaping.

	$s_{\rm A}(t)$,
	$s_{\rm B}(t)$,
	$s_{\rm C}(t)$.

	$s_{\rm A}(t)$,
	$s_{\rm B}(t)$,
	$s_{\rm C}(t)$.