Exercise 3.5: Recursive Filters for GF(2)

General recursive filter (above)
and considered realization (below)

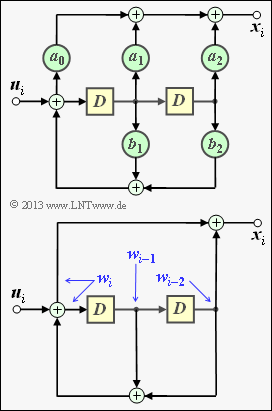
The upper of the two circuits on the right shows a second order recursive filter in general form. With

$$A(D) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} a_0 + a_1 \cdot D + a_2 \cdot D^2 \hspace{0.05cm},$$

$$B(D) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 1 + b_1 \cdot D + b_2 \cdot D^2 $$

one obtains for the transfer function

$$G(D) = \frac{A(D)}{B(D)} = \frac{a_0 + a_1 \cdot D + a_2 \cdot D^2}{1 + b_1 \cdot D + b_2 \cdot D^2} \hspace{0.05cm}.$$

It should be noted that all arithmetic operations refer to ${\rm GF(2)}$.

Thus, the filter coefficients $a_0, \ a_1, \ a_2, \ b_1, \ b_2$ are also binary $(0$ or $1)$.

The bottom graph shows the filter specific to the exercise at hand:

A filter coefficient results in $a_i = 1$ if the connection is through $(0 ≤ i ≤ 2)$.
Otherwise, $a_i = 0$. The same system applies to the coefficients $b_1$ and $b_2$.

In the subtasks (1), ... , (3) you are to determine the respective output sequence $\underline{x}$ for different input sequences

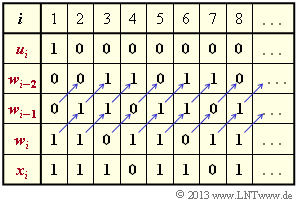
$\underline{u} = (1, \, 0, \, 0, \, 0, \, 0, \, 0, \, 0, \, 0, \, \text{...}\hspace{0.05cm})$,

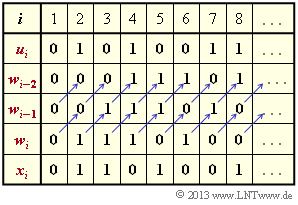
$\underline{u} = (0, \, 1, \, 0, \, 1, \, 0, \, 0, \, 1, \, 1, \, \text{...}\hspace{0.05cm})$,

$\underline{u} = (1, \, 1, \, 1, \, 0, \, 0, \, 0, \, 0, \, 0, \, \text{...}\hspace{0.05cm})$

using the given circuit. It should be taken into account:

If the input sequence $\underline{u}$ consists of a "$1$" followed by all zeros, this specific output sequence $\underline{x}$ is the "impulse response" $\underline{g}$, and it holds:

$$\underline{g} \hspace{0.15cm} \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\hspace{0.15cm}{G}(D)\hspace{0.05cm}. $$

Otherwise, the output sequence results as the "convolution product" between the input sequence and the impulse response:

$$\underline{x} = \underline{u} * \underline{g} \hspace{0.05cm}.$$

The convolution operation can be bypassed with the "D-transform" .

Hints:

This exercise belongs to the chapter "Algebraic and Polynomial Description".

Reference is made in particular to the section "Filter structure with fractional–rational transfer function"

Solution

(1) Correct are the proposed solutions 2 and 3:

To calculate the impulse response $\underline{g}$

The impulse response $\underline{g}$ is equal to the sequence $\underline{x}$ for the input sequence $\underline{u} = (1, \, 0, \, 0, \, \text{...})$. Based on the filter structure, $w_0 = w_{-1} = 0$ and the equations

$$w_i \hspace{-0.2cm} \ = \ \hspace{-0.2cm} u_i + w_{i-1} + w_{i-2} \hspace{0.05cm},$$

$$x_i \hspace{-0.2cm} \ = \ \hspace{-0.2cm} w_i + w_{i-2} $$

the result $\underline{g} = \underline{x} = (1, \, 1, \, 1, \, 0, \, 1, \, 1, \, 0, \, 1, \, \text{...})$ corresponding to proposed solution 2, as shown in the adjacent calculation.

But additionally the proposed solution 3 is correct, because one recognizes from this calculation scheme further following periodicities of the impulse response $\underline{g}$ (up to infinity) because of in each case same register assignment:

$$g_3 \hspace{-0.2cm} \ = \ \hspace{-0.2cm} g_6 = g_9 = \hspace{0.05cm}\text{...} \hspace{0.05cm}= 1 \hspace{0.05cm},$$

$$g_4 \hspace{-0.2cm} \ = \ \hspace{-0.2cm} g_7 = g_{10} =\hspace{0.05cm} \text{...} \hspace{0.05cm}= 0 \hspace{0.05cm},$$

For calculation of the output sequence $\underline{x}$

$$g_5 \hspace{-0.2cm} \ = \ \hspace{-0.2cm} g_8 = g_{11} =\hspace{0.05cm} \text{...} \hspace{0.05cm}= 1 \hspace{0.05cm}.$$

(2) After similar calculations as in subtask (1) one recognizes the correctness of solutions 1 and 3:

The initial sequence $\underline{x}$ also extends to infinity.
Periodicities show up again.

The same result is obtained by adding the impulse responses $\underline{g} = (1, \, 0, \, 1, \, 0, \, 1, \, 1, \, 0, \, 1, \, \text{...} \hspace{0.05cm})$ n the Galois field ${\rm GF(2)}$ shifted by one, three, six, and seven positions (to the right, respectively):

$$\underline{x} = (0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 1 \hspace{0.05cm}\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} \text{...}\hspace{0.05cm}) \hspace{0.05cm} + \hspace{0.05cm} (0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm}0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 1 \hspace{0.05cm}\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm} \text{...}\hspace{0.05cm}) \hspace{0.05cm} + \hspace{0.05cm} (0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm}0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0 \hspace{0.05cm}\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm} \text{...}\hspace{0.05cm}) \hspace{0.05cm} + \hspace{0.05cm} (0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm}0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0 \hspace{0.05cm}\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm} \text{...}\hspace{0.05cm}) $$

$$\Rightarrow \hspace{0.3cm}\underline{x} = (0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0 \hspace{0.05cm}\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm} \text{...}\hspace{0.05cm}) \hspace{0.05cm}. $$

Due to the linearity of the system under consideration, this is allowed.

(3) Here we choose the way over the $D$ transforms:

$$\underline{u}= (\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm}) \quad \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\quad U(D) = 1+ D + D^2 \hspace{0.05cm}.$$

With the transfer function $G(D) = (1 + D^2)/(1 + D + D^2)$ one thus obtains for the $D$ transform of the output sequence:

$$X(D) = {U(D)} \cdot G(D) = {1+D+D^2} \cdot \frac{1+D^2}{1+D+D^2} = 1+D^2 \hspace{0.05cm}\hspace{0.3cm} \Rightarrow \hspace{0.3cm}\underline{x} = (1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0 \hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0 \hspace{0.05cm}\hspace{0.05cm},\hspace{0.01cm} \text{...}\hspace{0.05cm} \hspace{0.05cm} ) \hspace{0.05cm}.$$

Only the proposed solution 1 is correct here: despite infinitely long impulse response $\underline{g}$, for this input sequence $\underline{u}$ the output sequence $\underline{x}$ is limited to three bits.

The same result is again obtained by adding shifted impulse responses:

$$\underline{x} = (1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0 \hspace{0.05cm}\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} \text{...}\hspace{0.05cm}) + (0\hspace{0.05cm},\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0 \hspace{0.05cm}\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} \text{...}\hspace{0.05cm}) + (0\hspace{0.05cm},\hspace{0.05cm}0\hspace{0.05cm},\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0 \hspace{0.05cm}\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm} \text{...}\hspace{0.05cm}) = (1\hspace{0.05cm},\hspace{0.05cm}0\hspace{0.05cm},\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0 \hspace{0.05cm}\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm}0\hspace{0.05cm},\hspace{0.05cm} \text{...}\hspace{0.05cm}) \hspace{0.05cm}. $$

$\rm GF(2)$ polynomial division $(1 + D^2)/(1 + D + D^2)$

(4) Correct are the proposed solutions 1 and 3:

On the data sheet, the general transfer function of a second–order recursive filter is given as follows.

$$G(D) = \frac{a_0 + a_1 \cdot D + a_2 \cdot D^2}{1 + b_1 \cdot D + b_2 \cdot D^2} \hspace{0.05cm}.$$

Das hier betrachtete Filter ist durch die Koeffizienten $a_0 = a_2 = b_1 = b_2 = 1$ und $a_1 = 0$ bestimmt. Somit erhält man das Ergebnis entsprechend dem Lösungsvorschlag 1:

$$G(D) = \frac{1 + D^2}{1 + D + D^2} \hspace{0.05cm}. $$

At the same time $G(D)$ is also the $D$ transformed of the impulse response:

$$\underline{g}= (1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0 \hspace{0.05cm}\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm}1\hspace{0.05cm},\hspace{0.05cm}0 ,\hspace{0.05cm} \text{ ...}\hspace{0.05cm}) \hspace{0.15cm} \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\hspace{0.15cm} {G}(D)$$

$$\Rightarrow\hspace{0.3cm} {G}(D)= 1 + D + D^2 + D^4+ D^5 +\text{...} \hspace{0.1cm}. $$

This means: The proposed solution 3 is also correct.
The same result would have been obtained by dividing the two polynomials $1 + D^2$ and $1 + D + D^2$, as the calculation opposite shows.

	It holds $\underline{g} = (0, \, 1, \, 1, \, 0, \, 1, \, 0, \, 0, \, 1, \, \text{...}\hspace{0.05cm})$.
	It holds $\underline{g} = (1, \, 1, \, 1, \, 0, \, 1, \, 1, \, 0, \, 1, \, \text{...}\hspace{0.05cm})$.
	The impulse response $\underline{g}$ is infinitely extended.

	The output sequence is: $\underline{x} = (0, \, 1, \, 1, \, 0, \, 1, \, 0, \, 0, \, 1, \, \text{...}\hspace{0.05cm})$.
	The output sequence is: $\underline{x} = (1, \, 1, \, 1, \, 0, \, 1, \, 1, \, 0, \, 1, \, \text{...}\hspace{0.05cm})$.
	The output sequence $\underline{x}$ extends to infinity.

	The output sequence $\underline{x}$ starts with $(1, \, 0, \, 1)$.
	The output sequence $\underline{x}$ begins with $(1, \, 1, \, 1)$.
	The output sequence $\underline{x}$ extends to infinity.

	It holds $G(D) = (1 + D^2)/(1 + D + D^2)$.
	It holds $G(D) = (1 + D + D^2)/(1 + D^2)$.
	It holds $G(D) = 1 + D + D^2 + D^4 + D^5 + D^7 + D^8 + \hspace{0.05cm} \text{...}\hspace{0.05cm} $ .